Разработка нового стахостического метода управления очередями заданий с использованием Марковских процессов для параллельных вычислений на кластере

Аннотация

А.А. Аль-Хулайди

В статье рассматривается задача оптимизации распределения заданий по исполнителям в кластере. В работе также устанавливаются критерии для  разрабатываемого алгоритма распределения.  Для решения задачи использовалась теория массового обслуживания, теория параллельного программирования, теория Маркова.
Ключевые  слова:  кластеризация, теория массового обслуживания (ТМО), планировщик задач, менеджер ресурсов,  цепи Маркова.                   

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Введение
В последние годы за рубежом и в нашей стране активно ведутся работы, связанные с использованием технологии параллельной обработки[1].
С использованием параллельной обработки, возможно значительно повысить скорость выполнения работы. Поскольку суперкомпьютеры остаются достаточно дорогими, только большие компании и институты способны обладать такими вычислительными возможностями. Решением этой проблемы является кластеризация законченных процессорных единиц воедино. Таким образом возможно создание системы, вычислительная мощность которой будет сравнима с суперкомпьютером, а стоимость значительно меньше.
Постановка задачи. Существует проблема при организации параллельных вычислений  в кластерном пакете mpich, а именно  отсутствие организаций очередей заданий. В данной работе ставится задача разработать расширение для пакета mpich, позволяющая осуществлять управление очередями заданий в кластере локальной сети. Для этого был разработан новый стохастический метод управления очередями  с использованием Марковских процессов.
Maui
Планирование основано на придании процессам некоторых значений приоритетов процессам в соответствующей очереди. Возможно использование планировщика Maui, разработанного Maui Supercomputing center. Планировщик Maui предоставляет контроль над тем, в какое время, где и как такие ресурсы как процессоры, память и дисковое пространство выделяются заданиям.[2]Дополнительно к этому управлению, он также предоставляет механизм, который помогает продуманно оптимизировать использование этих ресурсов и общий менеджмент системы. Основное преимущество использования планировщика – это легкость настройки путем манипулирования элементарными объектами.
Менеджер ресурсов Torque
Менеджер ресурсов предоставляет низкоуровневую функциональность для запуска, сохранения, остановки и мониторинга заданий. Без этих способностей ни один планировщик не может управлять заданиями. В дополнение к Maui наш кластер будет использовать Torque как Менеджер ресурсов. [3] Это означает, что с момента, когда задание запущено пользователем, Torque будет обрабатывать всё от старта до выполнения. Организация пула ресурсов в групповых системах обычно ограничивает их техническое администрирование, предоставляя их пользователям в единой форме.
Классификация систем массового обслуживания.
Идентификация элементов этой классификации предоставляет символическую  систематику, представленную в вариантах элементов системы.  Классификация  существует в нескольких модификациях.
Наиболее подходящая к рассматриваемым кластерным системам использует 6 символов.
A/B/s/q/c/p
Первый символ ‘A’ определяет природу входящего процесса. Обычно мы предполагаем, что интервал между поступлением заданий независим и имеет равномерное распределение. Второй символ ‘B’ определяет природу времени обслуживания. Он также предполагается независимым, равномерно распределенным и независимым от интервала между поступлением заданий. Третий символ ‘s’ представляет собой число параллельных серверов. Четвертый символ ‘q’ описывает дисциплину очереди. Зависит от того, как клиент трактует FCFS, LCFS и т.д. Пятый символ определяет максимально возможное число клиентов в системе (ожидающих и обслуживаемых), то есть ёмкость системы. Последний символ представляет собой число потенциальных клиентов. Если это число имеет тот же порядок, что и число серверов, то число потенциальных клиентов предполагается бесконечным. После анализа выполнения заданий на разработанной модели мы можем заключить, что интервалы между поступлением заданий и время обслуживания являются независимыми случайными величинами, имеющими экспоненциальное распределение. Модель  использует дисциплину очереди неупреждающих приоритетов. Таким образом, по классификации система может быть описана как:
M/M/c/Pnp/∞/∞,
где с равно 192(48 узлов * 4 логических процессора).
Система, подобная этой,   называется Марковской, что происходит из факта, что экспоненциальное распределение является непрерывным с Марковским свойством. Мартовское свойство состояний состоит в том, что распределение системы на следующем шаге (и фактически все будущие шаги) зависят только от текущего состояния системы, и состояние на предыдущих шагах не имеет значения.
Оценка параметров производительности системы
Поскольку классификация нашей ожидающей очереди определена, мы в дальнейшем будем описывать свойства системы. Из марковского свойства нашей системы мы сделаем следующие выводы:

1. Состояние системы может быть обобщено в одной переменной, называемой числом клиентов в системе,
2. Марковские системы могут быть напрямую проецированы на марковскую цепь с непрерывным временем (CTMC), которая может быть разрешена.
3. Для марковских систем вероятность перехода на n шагов P_ij (то есть вероятность того, что марковская цепь будет находиться в конечном состоянии j после n переходов из начального состояния i) будет стремиться к пределу πj с ростом t и будет независимым от начального состояния i. Этот предел называется установившимся состоянием или равновесной вероятностью состояния j.

В нашем случае установившееся состояние означает, что в некоторый момент в будущем, j заданий будут присутствовать в системе. Мы можем получить вероятность устойчивого состояния используя уравнения Эрланга для нашей системы. Как только устойчивое состояние определено, другие важные параметры производительности легко могут быть определены. Один важный фактор – это используемость. Используемость процессора – это один из факторов, используемый для оценки качества одной системы по отношению к другой. Другой вычисляемый параметр  – среднее число клиентов, присутствующих в системе:
L =             (1)
В случае нас интересует число ожидающих заданий, находящихся в очереди Lq . Мы можем найти  Lq , также выведя его из устойчивого состояния.
L =     (2)
На основе статистических данных использования модели системы можно определить темп поступления заданий λ и темп обслуживания системой. В соответствии с законом Литтла мы можем сказать, что среднее время, которое задание проводит в системе
           (3)
Дополнительно мы можем вычислить среднее время, которое задание проводит в очереди W_q, применив закон Литтла к L_q вместо L.  Когда идет речь о стремлении повысить используемость процессоров, это может быть сделано путем настройки правильных параметров для планирующего программного обеспечения, в нашем случае Maui. Главной целью системы управления с очередью – это уменьшение времени ожидания заданий в очереди. Отсюда следует, что  W_q будет использоваться. Возможно деление заданий на группы по различным принципам. Сначала мы разделим задания на две группы. Первая содержит последовательные задания, вторая – соответственно параллельные задания. Для каждой группы мы вычислим Wq для различных количеств узлов, доступных для этой группы. Теперь мы добавим W_qsn и W_qp(48-n)   , где s и p обозначают тип задания и n равно числу используемых узлов. Оптимальное решение может быть найдено путем поиска такого n, при котором сумма W_qsn и W_qp(48-n)  будет минимальной. Смысл использования n, как числа узлов, а не числа процессоров состоит в том, что очереди статичны и поэтому один узел не может быть частью двух различных очередей. Такие же вычисления могут быть сделаны для групп, созданных путем деления всех заданий по принципу принадлежности к одному из департаментов (отделов), что может быть связано с политикой фирмы.
 Разработка алгоритма управления порядком запуска заданий
Данный алгоритм основан на алгоритме работы планировщика Maui. Планировщик работает итерационно, т.е. перемежая процесс планирования с ожиданием или выполнением внешних команд. Каждый цикл начинается при осуществлении одного из следующих событий:
·        меняется состояние задания или ресурса
·        достигнута граница резервирования
·        получена внешняя команда
·        с начала предыдущего цикла прошло время, определенное как максимальное.
После того как сделано некоторое, конфигурируемое количество резервирований, начинает работу собственно backfill. Он выясняет, какие узлы и на какое время, начиная с текущего, свободны. После этого свободные узлы объединяются в окна. Суммарная "ширина" окон может оказаться больше количества свободных в данный момент узлов, т.к. некоторые узлы могут входить в несколько окон.  Затем из всех окон выбирается одно, как правило, самое широкое. Среди всех оставшихся заданий выбирается наиболее точно удовлетворяющее этому «окну» задание и запускается. Если есть возможность, то запускается не одно задание. Так как при запуске заданий алгоритмом backfill учитываются сделанные ранее резервирования, то соответствующие им задания не будут задержаны.
Рассмотрим теперь один цикл работы планировщика. Он состоит из следующих шагов:

1. Получая сведения от системы пакетной обработки заданий (СПО) о машинах, стартовавших/закончившихся  заданиях, конфигурации системы, планировщик обновляет свою внутреннюю информацию о состоянии ресурсов.
2. Корректируются сделанные резервирования, исходя из обновленной информации о занятости узлов. Конкретнее – отменяются ранние резервирования, соответствующие уже завершившимся заданиям. На этой же фазе запускаются те ожидающие задания, время действия для которых уже наступило.
3. Далее из всего количества заданий, стоящих в очереди СПО, отбираются те, которые готовы к запуску в настоящий момент. При этом принимаются во внимание такие аспекты, как состояние задания (задержано  оно или нет), достаточно ли ресурсов всего кластера для запуска этого задания и т.п. После этого из получившегося списка отсеиваются задания в соответствии с политикой кластера.
4. Получившееся множество заданий упорядочивается в соответствии с приоритетами, которые назначаются исходя из ряда условий. В частности, принимаются во внимание запрашиваемые ресурсы, принадлежность задания тому или иному пользователю, историческая информация (кто сколько заданий запустил, чтобы избежать ситуации, когда кластер «оккупирован» кем-то, и недоступен для всех остальных).
5. Теперь в соответствии с полученным упорядоченным списком производится планирование. Задания рассматриваются, начиная с самого приоритетного. Последовательно получая  задания из списка, планировщик запускает их до тех пор, пока это возможно.

 Разработка алгоритма распределения ресурсов между процессами
Задание представляет собой абстрактную сущность, состоящую из набора команд и параметров. Задание представляется пользователю в виде скрипта, содержащего требования к ресурсам, атрибуты задания и набор команд, которые необходимо выполнить. Единожды создав скрипт задания, им можно пользоваться столько раз, сколько необходимо, также возможна его модификация. Задание сначала необходимо поставить в очередь планировщика, затем из этой очереди оно будет передано на один узлов для выполнения.
Задание может быть обычным (regular) и интерактивным (interactive). Обычное задание ставится в очередь и затем ожидает своего выполнения, результат будет записан в указанное пользователем место. Интерактивное задание отличается тем, что потоки ввода и вывода перенаправляются соответственно на экран и клавиатуру, соответственно, команды задания вводятся с клавиатуры непосредственно. Каждое задание может запросить для запуска множество разных ресурсов, таких как процессоры, память, время (обычное и процессорное). Также может понадобиться дисковое пространство. С помощью менеджера ресурсов можно установить лимит каждого ресурса. Если лимит не устанавливается для какого-либо ресурса, то он считается равным бесконечности. Алгоритм:

• Определяются типы ресурсов, используемых данным заданием, их количество, а также приоритет задачи.
• Задания распределяются по очередям (подгруппам) и упорядочиваются в порядке приоритета.
• Службе управления очередью отсылается исполняемый скрипт. Привязка к существующему резервированию осуществляется по ACL, т. е. резервирование ресурсов к этому моменту должно быть уже выполнено. Ресурсы могут быть следующих видов: количество процессоров, объем памяти, требуемое ПО, объем виртуальной памяти, количество времени и др.

Применение метода стохастического управления очередями в кластерном пакете MPI/MPICH обеспечивающий параллельных вычислений .
Практическая значимость работы заключается в том, что метод стохастического управления очередями был применён для расширения библиотеки mpich , и с её использованием было разработана параллельная программа для нахождения опорного плана в транспортной задачи  для кластера локальной сети.
Стохастическая транспортная задача
Стохастический вариант транспортных задач линейного программирования обеспечивает адекватное представление реальных задач организации транспортировок в системе «поставщик-потребитель».Начальные условия: m –поставщиков грузов и n потребителей;
 - объём груза, отправляемого от i- го поставщика, i -1,2,…,m;
 - объём груза доставляемого j потребителю, j=1,2,…,n;
 - плотность распределения случайной стоимости  транспортировки единицы груза от i-го поставщика к  j –  потребителю, i  = 1,2,…,m , j = 1,2,…, n. План X=() должен удовлетворять естественным ограничениям:
 =ai, i = 1,2,…,m,    (4)
 =bi, j = 1,2,…,n,       (5)
xij ≥0, i = 1,2,…,m, j = 1,2,…,n.    (6)
Понятно, что любому плану X соответствует случайное значение суммарных транспортировок, равное  .           (7)
Вариант А. Найдем математическое ожидание для каждой из случайных величин cij : 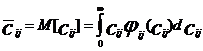    ,        (8)
i = 1,2,…,m, j = 1,2,…,n. Составим   .         (9)
Вариант В. С использованием плотностей распределения  найдём набор плотностей распределения случайных величин , а затем плотность распределения случайной суммарной стоимости транспортировок (7): 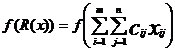.     (10)
P(R(x)≥ ) =  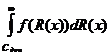        (11)
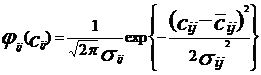,          (12)
Причём параметры  и , i = 1,2,…,m, j = 1,2,…,n, оцениваются статистически. В этом случае как известно 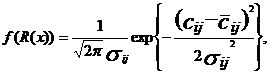           (13)
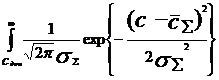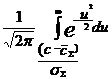Где      При этом  P(x≥ ) = dc=                                                      (14)
и задача минимизации сводится к максимизации функционала:
F(x)=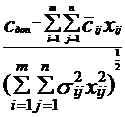.                     (15)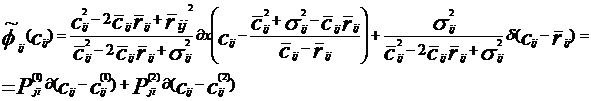

Проверка предложенных алгоритмов управления очередями на транспортной задаче
Для оценки практической значимости работы требовалось провести испытание разработанной программы с применением библиотек MPICH и новый разработанный MPI/MPICH_NEW (который содержит разработанные алгоритмы управления очередями ).
Испытания проводились в три этапа. На первом этапе   при увеличении размерности задачи
50x50, 70x70 и число процессов 20 прирост производительности не изменяется.
На втором этапе при  увеличении размерности задачи 100x100,150х150 ,500х500 и число процессов 20  прирост производительности  становится более заметным (в  1,07 раз быстрее при расчете матрицы размера 500x500).На третьем этапе при  увеличении числа процессов с 20 до 40 рост производительности становится более заметным (в 1,13 раз быстрее чем при расчете матрицы размера 1000x1000). Выполнение производилось на 4-х машинах с двухъядерным процессором Intel Core 2 Duo E6700 и 2 Гб оперативной памяти приведены в табл.1. Время указано в секундах.
Табл. 1.
Результаты вычислительных экспериментов по исследованию  предложенных алгоритмов управления очередями задач в разработанный кластер MPI/MPICH_NEW  и проверка их  эффективности на  параллельном алгоритме нахождения опорного плана .

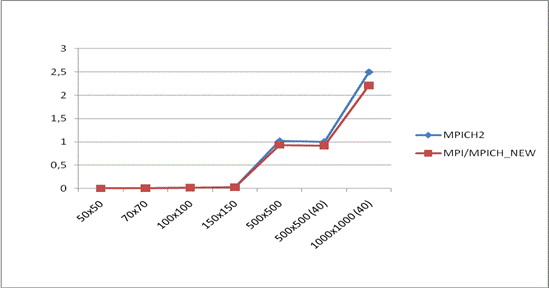
Рисунок 1. График времени выполнения программы в среде MPI после и до применения метода

Заключение

СПИСОК ЛИТЕРАТУРЫ
1. Аль-хулайди А.А.   Анализ существующих пакетов в кластерных сетях / А.А. Аль-хулайди, Н.Н. Садовой // Вестник Донского гос. техн. ун-та. — 2010. — Т. 10. — №3 (46). — С. 303–310.
2.Maui administrator’s guide. www.clusterresources.com (дата обращения 15.07.2010) 3.Torque administrator’s guide. www.clusterresources.com (дата