Анализ коррозионного износа нагруженного полого шара
Аннотация
В работе рассматривается поведение полого шара нагруженного внешним и внутренним давлениями. Кроме того, в полости происходит равномерно распределенный по поверхности коррозионный износ, приводящий к увеличению объема полости. Из решения задачи определяется предельное значение времени, соответствующее достижению второго инварианта тензора напряжения предельному значению для точек полости.
Ключевые слова: коррозия, износ, полый шар, предельное давление, предельное время.Ключевые слова:
Введение. При транспортировки агрессивных сред обычно используют тару, форма который не имеет угловых точек т.к. такого типа точки являются концентраторами коррозии [1]. Поведение конструкции в этих точках моделируется поведением сопряжения элементов, которые описываются элементами сферической поверхности. Поэтому при расчете таких сосудов на прочность применяются решения соответствующих задач для элементов шара. Учитывая важность задач на прочность тар для транспортировки агрессивных сред, расчет шара с полостью, подверженного коррозионному износу, представляется актуальным.
Кроме того, такого типа задачи встречаются при проектировании покрытий. С учетом некоторых технологий нанесения покрытия в нем возникают повреждения, которые описываются порами, имеющими сферообразную форму. В результате действия агрессивных сред на это покрытие происходит диффузия «агента», что приводит к концентрации агрессивной среды в порах. Под действием происходящей коррозии увеличивается объем пор, что объясняется коррозионным износом [1]. Поэтому, при сжатии покрытия некоторой нагрузкой, в некоторой момент времени, происходит его разрушение. Таким образом, разрушение покрытия происходит в зависимости от нагрузки и от времени коррозии. Для установления этих зависимостей можно рассмотреть выше приведенную задачу, как простейшую модельную задачу.
Таким образом, для обеих задач интерес представляет определение значений времени коррозии и нагрузки, при которых происходит разрушение шара.
Постановка задачи. Рассмотрим упругую сферу с центром в точке 
и радиуса 
. Предположим, что в ней имеется сферическая полость с центром в этой же точке 
и радиуса 
. Пусть это тело находится под действием радиальных равномерно распределенных по поверхностям силы с интенсивностью 
и 
, приложенных соответственно, к внешней поверхности и внутренней полости. Предположим, что во внутренней полости шара находиться агрессивная среда, приводящая к равномерно распределенной по поверхности внутренней коррозии. Пусть в результате коррозии происходит лишь износ внутренней поверхности, т.е. изменение радиуса 
и это изменение 
равномерно распределено по поверхности т.е. 
и не зависит от координат точки поверхности 
. Исследуем поведение рассмотренного шара во времени 
.
Решение задачи. Для этого введем сферическую систему координат с центром в точке 
. Не смотря на то, что состояние шара изменяется во времени 
, предположим, что рассматриваемое тело находиться в равновесии. В начале, рассмотрим равновесие без учета износа. Уравнение равновесия в напряжениях имеет вид [2]
(1)
где 
- сферические координаты, 
- физические компоненты тензора напряжения. Для решения уравнения (1) поставим граничные условия. Для рассматриваемого случая, исходя из условия нагружения, имеем
где 
не зависят от 
и 
. Изменение величины 
по времени т.е. величина 
определяется из уравнения коррозии поверхности 
. Исходя из условий нагружения и коррозии, можно предположить, что эта задача осесимметричная, т.е. можно принять, что 
и что 
. Тогда из уравнения равновесия следует:
; 
; 
(2)
Рассмотрим соотношения между физическими компонентами тензора деформации 
и физическими компонентами вектора перемещения 
.
В общем случае они имеют следующий вид [2]:
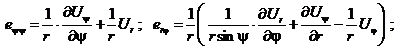
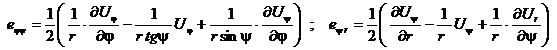
В рамках предположения осесимметричности т.е. приняв, что 
,
эти соотношения упростятся следующим образом
Физические соотношения рассматриваемого тела возьмем в следующем виде, считая материал шара изотропным, упругими не зависящим от коррозии:
где 
и 
- коэффициенты Ляме. С учетом приведенных соотношений уравнение (2) упростится следующим образом:
После интегрирования имеем:
,
где 
- постоянные интегрирования, которые определяются из граничных условий. С учетом вида 
имеем:
Полученная система линейных неоднородных алгебраических уравнений относительно 
позволяет определить искомые величины. Тогда решение уравнения равновесия можно записать в виде:
(3)
Зная решение уравнения равновесия (3), можно определить любую величину напряженно-деформированного состояния в произвольной точке тела. Выражение (3) применяется при рассмотрении коррозии на внутренней поверхности шара. В этом случае необходимо величину 
заменить на 
.
Тогда в выражении (3) неизвестной величиной является функция 
. Определение этой величины имеет смысл, если конструкция не потеряла свою несущую способность до начала коррозии, в частности, не разрушилась под действием приложенных сил 
. Из теории разрушения имеем, что конструкция не разрушается, если 
, где 
- второй инвариант тензора напряжения,
- предельное значение напряжения [3]. (Приведенное неравенство может определять начало образования пластической зоны, если 
, где 
- предел текучести). Из определения второго инварианта тензора напряжения следует:
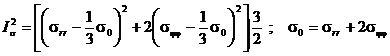
После преобразования, применительно к рассматриваемой задаче, до начала коррозии, имеем
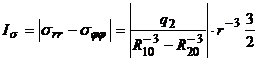(4)
Так как начало разрушения соответствует наибольшему значению
, то из равенства (4) следует, что разрушение начинается при 
и
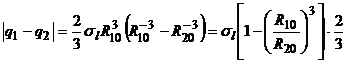(5)
Равенство (5) определяет допустимое значение нагружения, т.е. такое значение нагружения, при котором шар разрушается до начала коррозии.
Рассмотрим процесс внутренней коррозии не нагруженного полого шара. Тогда уравнение коррозии тела произвольной формы, для простейшей модели, возьмем в виде [1]:
где 
- объем тела, 
- объем тела до коррозии, 
- скорость коррозии, зависящая от физико-химических свойств пары среда-материал тела. Применительно к полому ненагруженному шару имеем, что
Тогда из уравнения коррозии, после интегрирования по 
и с учетом начального условия, следует:
После преобразования получим:
. (6)
Полученное выражение определяет зависимость радиуса полости шара от времени коррозии. Отметим, что для данной модели коррозии коррозионный износ сферической полости не зависит от радиуса внешней поверхности 
.
Анализ решения. Предположим, что шар вначале нагружен, а затем подвержен коррозии. Предположив, что коррозия не зависит от деформации, уравнение износа примет вид [4]:
или
(7)
При написании (7) были приняты следующие обозначения:
где 
и 
- радиусы сферических поверхностей с учетом коррозии и нагружения. Для малых перемещений в механике твердого деформируемого тела (линейная теория) принимается, что 
и 
. Отсюда получается, что объем шара в результате нагружения не меняется. Тогда изменение объема нагруженного шара, вызванное коррозией, определяется уравнением (7), где принято, что 
; 
т.е. не зависит от нагрузки.
Выражение (6) существует не для всех значений параметров задачи. Если шар не нагружена, то это выражение существует при 
т.е. до полного износа шара. Время полного износа шара, определяемое из условия 
, равно
.
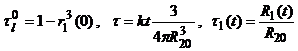Если шар нагружен, то, как было показано выше, существует допустимое значение нагрузки, соответствующее разрушению шара. Так как 
не меняются в процессе износа и с возрастанием времени, коррозия величина 
возрастает, то происходит утончение шара, приводящее к разрушению шара при нагрузке меньше допустимой. Значение 
, при котором происходит разрушение, основываясь на (5), определяется из следующего уравнения:
.
Здесь предполагается, что 
не зависит от коррозии [4]. Тогда предельное значение времени 
, при котором происходит разрушение, основываясь на (6) определяется из следующих уравнений:
.
Искомое значение времени равно:
(8)
Уравнение (8) позволяет, зная величины 
, определить длительность коррозии, при котором происходит разрушение, т.е. величину 
. На графике 1 приведена зависимость 
от значений действующих нагрузок, т.е. от 
для различных значений начального геометрического параметра шара 
. Отметим, что при 
шар нагружен, а время разрушения равно времени полного износа не нагруженного шара.
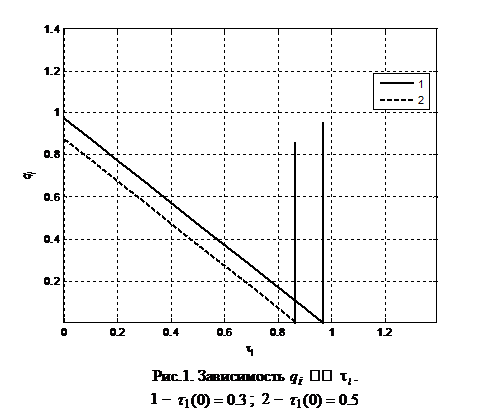
Из графика следует, с возрастанием разности давлений время разрушения уменьшается. Вертикальные (штрих) линии соответствуют времени полного коррозионного износа не нагруженного шара. С убыванием значения начального геометрического параметры шара время разрушения возрастает при фиксированных значениях давлений.
Уравнение (8) позволяет определить начальное значение геометрического параметра шара, при котором произойдет его разрушение для заданных значений нагрузок за заданное время коррозии. Из (8) следует
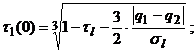(9)
На графике 2 приведена зависимость 
от времени разрушения для различных значений действующих нагрузок.
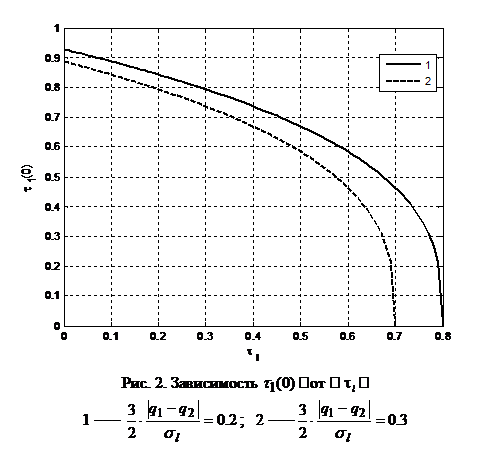
Из графика следует, что с возрастанием времени разрушения значение начального геометрического параметра шара убывает. Кроме того, увеличение разности давлений приводит к уменьшению значения начального геометрического параметра при фиксированном значения времени разрушения.
Выводы. В работе рассматривается поведение полого шара, нагруженного внешним и внутренним давлениями. Кроме того, в полости шара происходит равномерно распределенный по поверхности коррозионный износ, приводящий к увеличению объема полости. Из решения задачи определяется предельное значение времени, соответствующее достижению второго инварианта тензора напряжения предельному значению для точек полости, т.е. разрушение шара под действием коррозии и давлений. Кроме того, найдены допустимые значение нагрузки и геометрических параметров шара, при которых предельные значения времени существуют.
Литература
1.Скорчеллетти В.В. Теоретические основы коррозии металлов. Л.:«Химия»,1973, 263с.
2. Амензаде Ю.А. Теория упругости. М.: Высшая школа, 1976, 272 c.
3. Карпенко Г.В. Прочность стали в коррозионном среде. М., Машгиз, 1963, 188 с.
4. Логан Х.Л. Коррозия металлов под напряжением. М.:«Металлургия», 1970, 340 с.