Влияние многозарядных примесных центров на распределение потенциала в приповерхностной области полупроводника
Аннотация
Дата поступления статьи: 16.02.2013Разработана математическая модель распределения потенциала в приповерхностной области полупроводника при наличии в его запрещенной зоне глубоких энергетических уровней, обусловленных многозарядными примесными центрами. Результаты моделирования могут быть использованы для оценки ширины области пространственного заряда, прогнозирования наиболее вероятного механизма переноса носителей заряда в структуре металл-полупроводник с многозарядными глубокими энергетическими уровнями, а также величины барьерной емкости, что может найти применение при разработке приборов твердотельной электроники с улучшенными значениями отдельных параметров.
Ключевые слова: уравнение Пуассона, многозарядный примесный центр, распределение потенциала, глубокие энергетические уровни
Кристаллографические дефекты оказывают существенное влияние на характеристики полупроводниковых приборов, элементов интегральных схем, а также во многом определяют процент выхода годной продукции. Процесс изготовления структур твердотельной электроники включает последовательность сложных физико-химических операций, каждый этап которой сопровождается формированием различных, как желательных, так и нежелательных кристаллографических дефектов, характерных именно для данного этапа [1, 2]. Примеси и дефекты играют определяющую роль в рекомбинационных процессах.
Дефекты, взаимодействующие с носителями заряда, принято называть электрически активными. Некоторые из них образуют в запрещенной зоне полупроводника глубокие энергетические уровни (ГУ), которые характеризуются такими параметрами как энергия ионизации Еt, концентрация Nt, сечение захвата σt.
В работах [3 – 7] представлены физико-математические модели и проведено моделирование электрофизических свойств и характеристик структур металл-полупроводник с барьером Шоттки, структур металл-диэлектрик-полупроводник, а также транзистора с металлической базой. При моделировании учитывалось наличие в запрещенной зоне полупроводника однозарядных ГУ, обусловленных электрически активными примесями и несовершенством его кристаллического строения, а также неоднородность их пространственного распределения. В ряде случаев энергетический спектр примесного полупроводника оказывается более сложным и характеризуется несколькими уровнями в запрещенной зоне [8, 9]. В частности, сложным спектром обладают атомы примеси переходных металлов в кремнии – медь, золото, железо, цинк и др (рис. 1).
Характеристики области пространственного заряда в полупроводниковой структуре, сформированной на основе полупроводника с ГУ, могут иметь существенные особенности, обусловленные перераспределениями носителей заряда. Это требует учета влияния ГУ при моделировании характеристик полупроводниковых приборов и структур, изготовленных на основе такого материала.
Известно, что атомы примесей, валентность которых отличается на единицу от валентности собственных атомов полупроводника, могут находиться только в двух состояниях – нейтральном и заряженном. При этом такой донор или акцептор, независимо от того, нейтрален он или заряжен, характеризуется одним энергетическим уровнем в запрещенной зоне полупроводника [4]. При одном и том же пределе растворимости примесей, формирующих в запрещенной зоне полупроводника ГУ, наибольшее влияние на распределение потенциала будут оказывать многозарядные ГУ.
В спектре многозарядных примесей проявление энергетических уровней, обусловленных их наличием в полупроводнике, связано с сильным взаимодействием зарядов примесных центров [10]. Так, если один из энергетических уровней ![]() (
( ![]() ,
, ![]() - количество энергетических уровней, обусловленных многозарядным центром в запрещенной зоне полупроводника) уже занят электроном, а примесный центр
- количество энергетических уровней, обусловленных многозарядным центром в запрещенной зоне полупроводника) уже занят электроном, а примесный центр

Рис. 1. – Энергетические уровни различных примесей в кремнии [8]
захватывает еще один электрон на вышележащий энергетический уровень ![]() , то следует считать, что энергия уровня
, то следует считать, что энергия уровня ![]() уже не может проявиться в опытах из-за неразличимости между двумя электронами примесного центра Действительно, если электрон с уровня
уже не может проявиться в опытах из-за неразличимости между двумя электронами примесного центра Действительно, если электрон с уровня ![]() переводить в зону проводимости, то электрон с уровня
переводить в зону проводимости, то электрон с уровня ![]() перейдет на освободившийся уровень
перейдет на освободившийся уровень ![]() , передавая высвобождающуюся энергию электрону с уровня
, передавая высвобождающуюся энергию электрону с уровня ![]() . В результате на ионизацию израсходуется энергия, соответствующая
. В результате на ионизацию израсходуется энергия, соответствующая ![]() . Таким образом, существование энергетических уровней с энергией
. Таким образом, существование энергетических уровней с энергией ![]() определяется тем, занят электроном или нет, лежащий ниже уровень
определяется тем, занят электроном или нет, лежащий ниже уровень ![]() .
.
Для многозарядных центров концентрации носителей заряда на уровнях ![]() , взаимосвязаны и могут меняться при изменении положения уровня Ферми, температуры, величины поверхностного потенциала и т.п. Полная концентрация многозарядных примесных центров
, взаимосвязаны и могут меняться при изменении положения уровня Ферми, температуры, величины поверхностного потенциала и т.п. Полная концентрация многозарядных примесных центров ![]() может быть представлена в виде суммы концентраций многозарядных центров одного типа, находящихся в разных зарядовых состояниях [10]:
может быть представлена в виде суммы концентраций многозарядных центров одного типа, находящихся в разных зарядовых состояниях [10]:
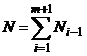 , (1)
, (1)
где ![]() - концентрация центров, характеризующихся величиной заряда (
- концентрация центров, характеризующихся величиной заряда (![]() ),
), ![]() - элементарный заряд.
- элементарный заряд.
При этом концентрация примесных центров ![]() , соответствующая уровню с энергией
, соответствующая уровню с энергией ![]()
![]() , (2)
, (2)
следовательно, концентрация ![]() -кратно ионизированных атомов может быть записана в виде произведения концентрации примесных центров
-кратно ионизированных атомов может быть записана в виде произведения концентрации примесных центров ![]() на вероятность их заполнения электроном
на вероятность их заполнения электроном ![]() :
:
![]() . (3)
. (3)
Решая систему уравнений (3) для ![]() , с учетом (1) и (2) можно определить концентрации центров
, с учетом (1) и (2) можно определить концентрации центров ![]() с зарядом (
с зарядом (![]() ).
).
Рассмотрим примесь меди в кремнии. Примесные центры меди в кремнии могут находиться в четырех состояниях: нейтральном, однократно, двукратно и трехкратно отрицательно заряженном. Тогда выражение (1) примет вид:
![]() ,
,
а система уравнений (3) с учетом (1) и (2)
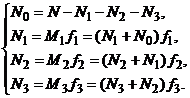 (4)
(4)
Решая систему уравнений (4) находим значения концентраций центров разной зарядовости:
![]() , (5)
, (5)
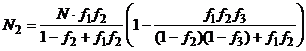 , (6)
, (6)
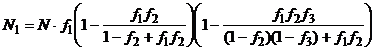 , (7)
, (7)
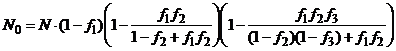 . (8)
. (8)
Полученные выражения (5) – (8) позволяют оценить концентрации трехкратно, двукратно, однократно ионизированных и электрически нейтральных атомов акцепторной примеси, формирующей в запрещенной зоне полупроводника три энергетических уровня ![]() ,
, ![]() ,
, ![]() соответственно. Выражения (5) – (8), могут быть упрощены в случае, если уровни
соответственно. Выражения (5) – (8), могут быть упрощены в случае, если уровни ![]() ,
, ![]() ,
, ![]() отделены друг от друга энергетическими зазорами много большими
отделены друг от друга энергетическими зазорами много большими ![]() , где
, где ![]() – постоянная Больцмана,
– постоянная Больцмана, ![]() – абсолютная температура. Тогда, например, если уровень Ферми находится между
– абсолютная температура. Тогда, например, если уровень Ферми находится между ![]() и
и ![]() , но достаточно далеко от обоих, можно считать, что
, но достаточно далеко от обоих, можно считать, что ![]() ,
, ![]() ,
, ![]() и из (5) – (8) получаем
и из (5) – (8) получаем ![]() ,
, ![]() ,
, ![]() ,
, ![]() , т.е. все центры находятся в зарядовом состоянии (
, т.е. все центры находятся в зарядовом состоянии (![]() ).
).
Рассчитаем распределение потенциала ![]() в кремнии легированном фосфором с концентрацией
в кремнии легированном фосфором с концентрацией ![]() , при наличии в нем примеси меди с
, при наличии в нем примеси меди с ![]() ,
, ![]() ,
, ![]() ,
, ![]() [6] (см. рис. 1.), решив уравнение Пуассона:
[6] (см. рис. 1.), решив уравнение Пуассона:
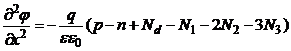 , (9)
, (9)
где ![]() – диэлектрическая проницаемость полупроводника;
– диэлектрическая проницаемость полупроводника; ![]() – электрическая постоянная;
– электрическая постоянная; ![]() ,
, ![]() – концентрации свободных дырок и электронов соответственно.
– концентрации свободных дырок и электронов соответственно.
В первом приближении вероятность ![]() заполнения электронами i-го акцепторного ГУ можно оценить выражением:
заполнения электронами i-го акцепторного ГУ можно оценить выражением:
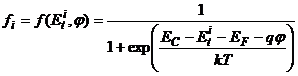 ,
,
Концентрации свободных носителей зарядов, а также ионизированных атомов мелкой донорной примеси в невырожденном полупроводнике можно определить, используя известную методику [8].
Распределения электростатического потенциала в приповерхностной области кремния для температуры Т = 300 К, при величине поверхностного потенциала ![]() приведены на рис. 2.
приведены на рис. 2.
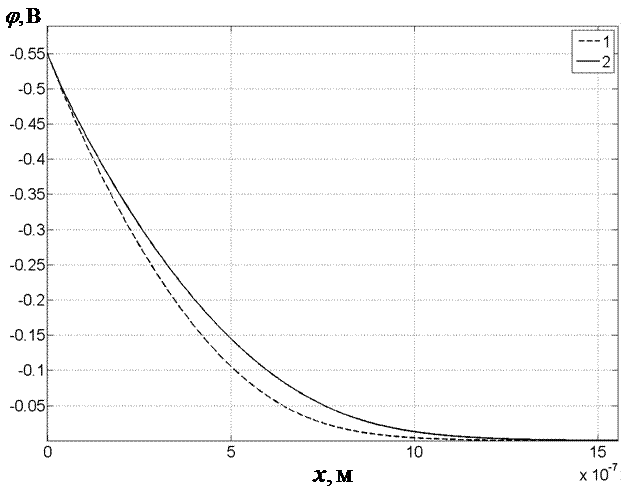
Рис. 2. – Распределение потенциала в области пространственного заряда полупроводника (1 – без ГУ в полупроводнике, 2 – в случае многозарядных ГУ, обусловленных примесью меди в кремнии).
Разработанная математическая модель позволяет оценить концентрации атомов многозарядных примесных центров, находящихся в различном зарядовом состоянии, а также их влияние на распределение потенциала в приповерхностной области полупроводника и как следует из [11, 12] актуальна при разработке перспективных элементов оптоэлектронных устройств.
Литература:
1. Адамов Ю.Ф., Верховцева А.В., Шурчков И.О., Балака Е.С. Анализ конструктивно-технологических ограничений при проектировании лавинных фотодиодов, работающих в режиме счета фотонов [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/788 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Борискин В.С., Гулякович Г.Н., Северцев В.Н. Организация мелкосерийного производства микросхем [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/789 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. Богданов С.А., Захаров А.Г. Моделирование распределения потенциала в приповерхностной области полупроводника с глубокими уровнями [Текст] // Известия ТРТУ. Технические науки. – 2005. – № 9. – C. 217–222.
4. Богданов С.А., Захаров А.Г. Вольт-фарадные характеристики МДП-структур с учетом однозарядного глубокого энергетического уровня [Текст] // Известия вузов. Северо-Кавказский регион. - 2007. - № 5. - С. 22–24.
5. Богданов С.А., Захаров А.Г., Котов В.Н. Моделирование распределения потенциала в барьерах Шоттки транзистора с металлической базой [Текст] // Нано- и микросистемная техника. - 2007. - № 4. - С. 45–47.
6. Богданов С.А., Захаров А.Г., Лытюк А.А. Моделирование распределения потенциала в барьерах Шоттки с учетом краевых эффектов [Текст] // Нано- и микросистемная техника. - 2011. - № 5. - С. 12–15.
7. Богданов С.А., Захаров А.Г., Лытюк А.А. Диффузионная модель процесса деградации контактов металл-полупроводник с барьером Шоттки // Известия ЮФУ. Технические науки. – 2012. - № 1. – С. 53 – 58.
8. Зи С.М. Физика полупроводниковых приборов [Текст] / М.: Энергия, 1973. – 656 с.
9. Gassoumi M., Bluet J.M., Guillot G., Gaquière C., Maaref H. Characterization of deep levels in high electron mobility transistor by conductance deep level transient spectroscopy [Текст] // Materials Science and Engineering: C. – 2008. Т. 28. № 5-6. – P. 787 – 790.
10. Рывкин С.М. Фотоэлектрические явления в полупроводниках [Текст] / М.: Физматгиз, 1963. – 496 с.
11. Lin S., Zeng S., Cai X., Zhang J., Wu S., Sun L., Zhang B. Simulation of doping levels and deep levels in InGaN-based single-junction solar cell [Текст] // Journal of Materials Science. - 2012. Т. 47. № 11. - P. 4595-4603.
12. Ali A., Asghar M., Gouveas T., Hasan M.-A., Zaidi S.H. Influence of deep level defects on the performance of crystalline silicon solar cells: experimental and simulation study [Текст] // Solar Energy Materials & Solar Cells. – 2011. Т. 95. № 10. – P. 2805 – 2810.