Математическое моделирование пылеулавливания в технологических системах, уменьшающих выбросы дисперсных частиц в атмосферу
Аннотация
Приводится методика построения математической модели для решения задач анализа и прогнозирования распространения жидкостей в трехмерных пористых средах, дается краткое описание разработанных моделей и закономерности движения жидкости на основе применения фрактальных кластеров. Ключевые слова: фрактал, загрязнение, загрязняющая жидкость, перколяция, фрактальный кластер, фронт заражения, трехмерная динамическая решеточная модель
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Южно-Российский государственный технический университет
Проблема очистки газовых потоков от дисперсной компоненты (пыли) имеет принципиальное значение для обеспечения безопасной среды обитания человека. Речь идет не только об улучшении качества производственной среды [1], но и снижении биосферных рисков [2]. Разработка эффективных устройств, совершенствование отдельных элементов средств пылеподавления требует технических и конструктивных поисков. До сих пор эти поиски имели экспериментальную основу, что требовало больших материальных затрат и времени. В данной работе были созданы специальные программы, позволяющие посредством компьютерного моделирования произвести теоретический анализ эффективности пылеулавливания в зависимости от параметров конструкции установки. В отличие от прямого эксперимента разработанные программы позволяют перебрать в кратчайшие сроки большое количество разных вариантов параметров пылеулавливателя. Одна из программ позволяет посчитать долю захваченных пылеуловителем частиц в зависимости от длины и количества пылеподавляющих пластин. Вторая программа позволяет проанализировать эффективность различных геометрических конфигураций системы орошения водой газопылевого потока в пылеулавливателе.
На базе кафедры «Безопасность жизнедеятельности и охраны окружающей среды» ЮРГТУ (НПИ) были разработаны и запатентованы различные конструкции пылеподавляющих систем. Здесь использовался комплексный подход к пылеулавливанию – в одной и той же установке использовались различные методы захвата загрязняющих частиц.
Данные программы планируется использовать для дальнейшего совершенствования этих разработок.
В первой программе проводится моделирование взаимодействия загрязняющих частиц со специальными пылеподавляющими пластинами, расположенными внутри воздуховода.
После взаимодействия загрязняющих частиц часть из них останется на поверхности пластин, а часть проходит дальше. Методика очистки пластин после их использования заключается в применении связывающих жидкостей, которые собирают напыления и отводят их в специальные емкости.
На рисунке 1 показан характер движения частиц в конструкции пылеулавливателя с проникновением распыленных частиц из случайной точки пространства (слева) и из одной точки (справа).

Рис. 1. Характер движения частиц в пылеулавливателе
Цель проведения опытов заключается в подборе наиболее оптимальных характеристик пластин для задержания нужного количества частиц в зависимости от их поведения и потребности очистки.
В первом цикле экспериментов частицы произвольно размещались изначально в любой точки пространства и двигались по направлению пылеподавляющих пластин. На рисунке 2 показано распределение захваченных частиц на конструкции из 5 пластин, при этом всего запущено 209 частиц, из них прошли через пластины 33.
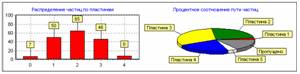
Рис. 2. Распределение частиц в пылеулавливателе из 5 пластин
На рисунке 3 показано распределение захваченных частиц на конструкции из 11 пластин, при этом всего запущено 500 частиц, из них прошли через пластины 4.

Рис.3. Распределение частиц в пылеулавливателе из 11 пластин
Во втором цикле экспериментов частицы размещались в центре пространства и двигались по направлению пылеподавляющих пластин. На рисунке 4 показано распределение захваченных частиц на конструкции из 5 пластин, при этом всего запущено 400 частиц, из них прошли через пластины 42.
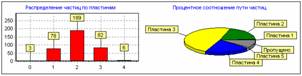
Рис. 4. Распределение частиц в пылеулавливателе из 5 пластин
На рисунке 5 показано распределение захваченных частиц на конструкции из 11 пластин, при этом всего запущено 600 частиц, из них прошли через пластины 14.

Рис. 5. Распределение частиц в пылеулавливателе из 11 пластин
Ряд поставленных экспериментов показывает характер распределения частиц на пластинах, интерпретация отображает найденные зависимости и математические законы распределения. Из рисунков видно, что зависимость имеет выраженный нормальный закон распределения, что характерно для наибольшей загрузки центральных пластин воздуховода. Приведенные в работе модели могут использоваться в задачах проектирования подобных воздухоочистителей путем задания количества пластин, их длины и расстояния между ними. В этом случае показанные исследования помогут найти оптимальную длину и взаимное расположение поверхностей пылеулавливающих пластин в конструкциях сложных воздуховодов.
Вторая программа моделирует другую стадию пылеулавливания, основанную на орошении загрязняющих частиц потоком жидкости. В программе генерируется поток капель воды. Каждая капля имеет определенный радиус, вектор координат и скорость, причем эти параметры задаются случайным образом, согласно определенному закону. Они выбираются так, чтобы общий поток капель имел конусообразную форму, характерную для распылителя. Так же капле задается ускорение, которое имеет постоянную величину. В итоге формируется совокупность виртуальных капель, движение которых призвано описать поведение реальных капель воды в распылителе. На рис. 6 изображен поток, состоящий из 3000 частиц. На этом рисунке видно, что сформированный поток имеет конусообразную форму, что соответствует форме реального потока.

Рис. 6 Смоделированный поток жидкости
После того, как смоделирован поток капелек воды, можно произвести расчеты, определяющие вероятность прохождения частиц пыли без столкновения с капельками воды. Случайным образом размещаются в плоскости сечения трубы 10000 пылинок и определяется факт столкновения частиц пыли с водой, при этом считается, что частица пыли движется строго по прямой вдоль трубы.
Определение факта столкновения сводится к задаче нахождения кратчайшего расстояния между прямой и точкой. Если это расстояние меньше чем радиус капельки воды, то пылинка столкнется с этой каплей.
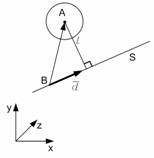
Рис. 7 Определение кратчайшего расстояния между прямой и точкой.
Кратчайшее расстояние определяется по формуле:
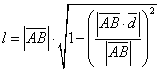
где:
A – точка центра капли воды.
B – одна из точек прямой S![]() - единичный вектор направляющей прямой S.
- единичный вектор направляющей прямой S.
Произведено с использованием данного подхода 10000 расчетов с разными координатами начального положения пылинки, и получен график вероятности столкновения пылинок с водой в зависимости от удаления от центральной оси трубы. Данный график представлен на рис. 8.
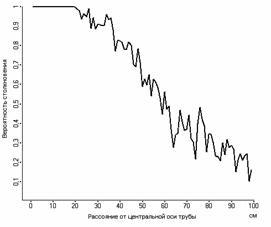
Рис. 8 График зависимости вероятности столкновения частицы воды с частицей пыли.
Из рис. 8 следует, что наиболее вероятно столкновение частиц пыли с водой на прямой центральной оси трубы, при условии, что распыление воды происходит из точки так же расположенной на этой оси. При удалении от центральной оси вероятность столкновения убывает достаточно монотонно. Наблюдаемые отклонения от монотонной зависимости имеют флуктуационную природу, связанную с пульсационными процессами в самом потоке. Характер самого падения отражает эпюру скоростей потока. Данная флуктуационная составляющая, наблюдается в реальных системах и не может быть в принципе получена аэрогидродинамическими методами.
На рис. 9 изображена динамика прохождения потока жидкости через пылевую стенку (Под пылевой стенкой понимается совокупность виртуальных частиц пыли, расположенных в одной плоскости). Видно как с течением времени пылевая стенка разрушается пылевым потоком. При этом число не захваченных частиц уменьшается с течением времени. График зависимости числа не захваченных частиц пыли от времени имеет вид кривой изображенной на рис. 10. Из рисунка видно, что кривая убывает монотонно и имеет закон убывания, близкий к логарифмическому.
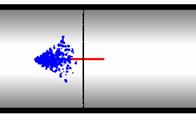
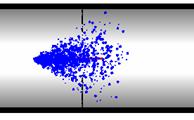
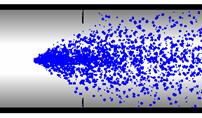
Рис. 9 Динамика процесса прохождения потока жидкости через пылевую стенку.
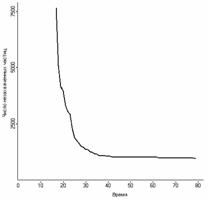
Рис.10 График зависимости числа не захваченных частиц от времени.
Помимо этого программа моделирует взаимодействие пылевых частиц с каплями жидкости, в условиях, когда скорость частиц пыли испытывает случайные пульсации.
В среднем движение частиц пыли в воздушном потоке происходит с постоянной скоростью. Сложная траектория движения отдельно взятой частицы достигается случайным изменением направления и величины вектора скорости этой частицы.
Если расстояние от центра некоторой капли до частицы пыли окажется меньше радиуса этой капли, то частица пыли считается захваченной, и она убирается из моделируемого процесса. Если пыль достигнет стенок трубопровода, то она так же считается захваченной и убирается из расчета.
Так мы можем получить картину прохождения «броуновской пыли» сквозь водяной поток.

Рис 11. Состояние прохождения моделируемой пыли сквозь водяной поток в разные моменты времени.
На рис. 11 представлен в виде ретроспективы характер движения пыли, полученный в ходе работы программы. Рисунок А соответствует начальному моменту времени, а рисунки Б, В, Г отображают состояние системы в более поздние моменты. Из рисунков следует, что по мере прохождения пыли сквозь водяной поток часть пыли захватывается каплями воды, причем в разных областях пространства имеется разная концентрация не захваченной пыли. Если считать степень прохождения пыли как процентное отношение начального числа частиц пыли к конечному числу, прошедшему сквозь водяной заслон расстояние 200см то оно составляет около 0,6% от начального числа.
Задавая различные положения форсунки, и меняя направление движения потока воды, можно получать разную степень захвата пыли. Это позволяет осуществлять подбор наиболее эффективного варианта расположения форсунок.
Таким образом, применение в этой программе метода Монте-Карло позволяет достаточно корректно моделировать процесс орошения газопылевого потока на линейном участке пылеулавливателя. Появляется возможность рассмотреть различные геометрические конфигурации потока капель жидкости. Метод учитывает явления, имеющие вероятностный характер. Это расширяет возможности выявления особенностей процессов взаимодействия пыли с частицами воды в системах орошения, которые не могут быть получены в детерминистких (аэродинамических) моделях.
Приведенные выше программы позволяют смоделировать наиболее часто применяющиеся методы пылеулавливания.
Список литературы
1. Фролов А. В. Безопасность жизнедеятельности. Охрана труда. Учебное пособие для ВУЗ-ов / А. В. Фролов, Т. Н. Балсаева; под ред. А. В. Фролова. – Ростов-на-Дону; Феникс, 2005. – 736 с.
2. Экология / под ред. проф. В. В. Денисова. – М.: ИКУ «МарТ», Ростов-на-Дону; Издательский центр «МарТ», 2006. – 768 с.
3. Ужов В. П. Борьба с пылью в промышленности. Госхимиздат,1962, 184с.
4. Трифонов К. И., Девисилов В. А. Физико-химические процессы в техносфере: Учебник. – М.: ФОРУМ:ИНФА-М, 2007. – 240с.
5. С. М. Ермаков, Г. А. Михайлов. Курс статического моделирования. – Главня редакция физико-математической литературы издательства «Наука», М., 1976г.
6. Алтунин А.Е., Семухин М.В. Расчеты в условиях риска и неопределенности в нефтегазовых технологиях: Монография. Тюмень: Издательство Тюменского государственного университета, 2004. 296 с.
7. С. М. Ермаков. Метод Монте-Карло и смежные вопросы. – Главная редакция физико-математической литературы изд-ва «Наука», 1975г.
20 июня 2008 г.