Моделирование «озоновой дыры», инициированной запуском ракеты-носителя

Аннотация

Д.С. Цымбалов

Разработана методика приближенного расчета динамики «озоновых дыр», возникающих при запусках жидкотопливных ракет-носителей. Ее основу составляют система эволюционных уравнений минимальной размерности, инициализированная в соответствии с предельно подробными моделями процесса. Надежно идентифицирован механизм возмущения стратосферной фотохимии при запусках жидкотопливных ракет. Ключевые слова: стратосфера, ракета-носитель, "озоновая дыра", траектория, факторизация

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Донской государственный технический университет,
Ростов-на-Дону

1. ВВЕДЕНИЕ

Проблема сохранения озонового слоя Земли в условиях интенсивного использования космического пространства с применением ракет требует развивать информационные модели влияния реактивных струй двигателей на стратосферные физико-химические процессы [1, 2]. Подобные модели [3-6] представляют собой большие системы эволюционных уравнений; динамическими переменными являются концентрации химических компонентов, поле солнечного излучения и параметры турбулентной диссипации. Анализ детальных моделей озоносферной динамики, возмущенной выбросами ракетн, проблематичен несмотря на прогресс вычислительной математики и связанных с ней информационных технологий. При этом особо востребованы простые модели и методы, которые позволили бы верно оценивать возмущение озоносферной динамики при различных сценариях использования ракетной техники [3].

Здесь предлагается удобный способ «упаковки» результатов детального компьютерного моделирования динамики неустойчивой озоновой дыры ракетного происхождения – в минимальную математическую модель, выражаемую системой двух обыкновенных дифференциальных уравнений. Одно из уравнений модели описывает кинетику стратосферного озона, а другое – его разрушителя совместно с диссипацией ракетного следа (РС).

С целью выявить ведущие механизмы эволюции ракетной «озоновой дыры», исследуя динамику подробной многокомпонентной диффузионно-кинетической модели [3], рассматривались следующие гипотезы: 1) вещество-разрушитель является химически стойким и, разрушая озон при химическом взаимодействии, само не разрушается (уменьшение концентрации разрушителя в этой модели обусловлено исключительно рассредоточением за счет турбулентных движений); 2) разрушающее озон вещество подвержено интенсивному распаду при взаимодействии с прочими (некритичными для наших целей) компонентами стратосферы, причем вклад стратосферного озона в гибель его разрушителя незначителен; 3) вещество-разрушитель избирательно реагирует исключительно в некаталитической реакции с озоном. Аккуратное исследование обозначенных эволюционных сценариев и сопоставление с результатами интегрирования детальных моделей ракетной «озоновой дыры» [3] позволяет утверждать, что воздействие реактивных струй жидкотопливных ракет-носителей (РН) на стратосферные процессы укладывается в сценарий 2). Также доказано [4], что даже простая «боксовая» модель ракетной «озоновой дыры» позволяет корректно воспроизводить эволюционный процесс.

2. МОДЕЛЬ ЭВОЛЮЦИИ «ОЗОНОВОЙ ДЫРЫ»

2.1. Основные уравнения

Динамические, тепловые процессы и реакции в следовом облаке РН описываются системой квазилинейных дифференциальных уравнений для концентрационных с(t) = ∪с_i(t) и температурного T(t) полей [3 - 4]

c_i = f_i(c, T, I_l,_H) ,     T = 1/c_P Sf_i(c, T, I_l,_H) ΔHi ,                (1)

где  – оператор, отвечающий за рассеивание примеси в «ящичной» постановке; f_i(c, T) и ΔH_i – соответственно скорость наработки и/или гибели i-го вещества в (фото-)химических реакциях и энтальпия его образования из простых веществ; I_λ ≡ I(λ, H) – интенсивность солнечного излучения в зависимости от длины волны λ и высоты H; c_P – теплоемкость воздуха и продуктов сгорания ракетных топлив (последние предполагаются совпадающими и не зависящими от температуры).

На раннем этапе диссипации РС перемешивание газа обусловлено остаточной энергетикой реактивной струи, на позднем – энергетикой стратосферной турбулентности. Поэтому процесс турбулентного размытия следового облака удобно аппроксимировать дифференциальным оператором

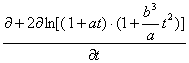 ≡  ,                                (2)

где t – время; a= Д/r_ini² и b = x/(3r_fin^2/3) – величины, обратные временам рассеивния следового облака на ранней и заключительной стадиях эволюции; r_ini и r_fin – минимальные радиусы следового облака, ассоциируемые с началом первичного и завершающего этапов диссипации; Д ≈ 10⁷ ÷ 10⁸ см²/с (для современных РН) – эффективный коэффициент диффузии; ξ – коэффициент горизонтального турбулентного переноса в стратосфере, равный удельной диссипации солнечной энергии в степени 1/3.

Для обозначения фоновых концентраций разрушителя и озона будем использовать соответственно с_ph и [O₃]_ph, их отклонения от равновесных (строго говоря, стационарных) значений – и ; прочие химически активные вещества обозначим символом М; константу скорости разрушения озона k, а константы скорости гибели вещества-разрушителя в реакциях первого и второго порядка соответственноk₁ и k₂. Безразмерное решение задачи об эволюции цилиндрически-симметричного следового облака (1) - (2) для химически инертной примеси обозначим как S(t): его явным выражением служит

S(t) =  1/(1 + at) (1 + b³/a t²) .                       (3)

2.2. Факторизация параметров первичного возмущения

Анализ опубликованных траекторных данных современных РН (см. рис. 1) позволяет использовать для высотно-скоростной зависимости физически обоснованную и достаточно простую общую формулу

,                            (4)

в которой скорость ракеты v и высота H имеют размерность м/с и м соответственно.

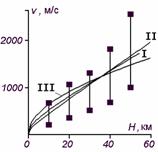
Рис. 1. Экспериментальные коридоры высотно-скоростной зависимости современных РН и вероятные теоретические траектории согласно (4): кривые I, II и III отвечают начальному ускорению ракеты g, g/2, и 2 g соответственно

Для стратосферного участка траектории выражение (4) упрощается и принимает вид

v(H) ≈ 0.025.(H + 10000) .                               (5)

С учетом (5) относительное уплотнение газа, его нагрев и насыщение нетипичными для стратосферы веществами даются следующими формулами:

Δr_H /r_H≈ 45.8·10⁶/[(9.8·10⁴– H)(H + 10000)] ,               (6)
ΔT_H /T_H≈ (9.8·10⁴– H)/(H + 10000) ,                               (7)
Δc_i,H/c_i,H≈ 1.15·10⁹/[(9.8·10⁴– H)(H + 10000)] .         (8)

В совокупности формулы (6) - (8) позволяют разделить количественные (массовые) и качественные (специфическое для ракет разных типов содержание химических веществ в реактивных газах) показатели первичного возмущения озоносферной динамики, что позволяет переносить результаты детального моделирования на сходные ситуации.

Практически важные химические характеристики возмущения озоносферы жидкотопливными ракетами приведены в таблице.

Таблица
Энерго-экологические характеристики первых ступеней современных ракет-носителей

2.3. Конкретные уравнения и начальные условия

С учетом введенных обозначений результаты наших ислдедований формулируются следующим образом. Совокупное (20 ≤ H ≤ 50 км) возмущение озоносферы РН описывается двумя уравнениями «кинетика – диффузия»

[NO] = – k_NO[M][NO] ,     [O₃] = – k_O3[O₃]_ph[NO] ,             (9)

с начальными условиями

[NO]|_t=0 = [NO]₀S(0) ,    [O₃]|_t=0 = [O₃]₀ S(0) .                      (10)

Уравнения (9) - (10) записаны для отклонений концентраций O₃ и NO от невозмущенных значений [O₃]_ph и [NO]_ph. В них использованы следующие обозначения: [O₃]₀ и [NO]₀ – соответственно начальные отклонения концентраций O₃ и NO в первичном РС от фоновых; подстрочный индекс «ph» приписывается невозмущенным или фоновым значениям концентраций ([NO]_ph – фоновая концентрация NO полагается нулю вследствие ничтожности по сравнению с начальной в ракетной следе [NO]₀); k_O3 и k_NO – (брутто)-константы гибели озона в системе реакций участием NO и гибели NO в реакциях со всевозможными веществами M; S(0) – начальное распределение примесей (продуктов сгорания) в стратосфере. Приведем явные выражения необходимых в дальнейшем автомодельных при t → ∞ концентрационных профилей S(t), частным случаем которых являются S(0). Поскольку практически интересна «долгосрочная» асимптотика турбулентной эволюции РС, пожертвуем деталями его ранней динамики и примем

S(t) =,                     (11)

где r₀ – поперечный размер РС в момент времени, выбранный начальным; b = ξ/(3r₀^2/3) – скорость турбулентной диссипации следового облака.

3. РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА И ИХ ИНТЕРПРЕТАЦИЯ

Решением задачи (4 - 6) служит

[O₃]( t) = {[O₃]₀ + k_O3[O₃]_ph[NO]₀/(k_NO[M]) ×
× [exp(–k_NO[M]t) – 1]} S(t) .                               (12)

Оно становится содержательным, если определить эффективные значения комплексовk_NO[M] и k_O3[O₃]_ph, сопоставив модельную кинетику (12) с данными детальных компьютерных расчетов [3-5]. Масштабные, уровневые и динамические параметры возмущения всего столба озоносферы ракетой «Протон» хорошо воспроизводятся уравнением (12), в котором k_NO[M] ≈ 10^-2 с^-1 и k_O3[O₃]_ph ≈ 10^-4 с^-1, [O₃]₀./[O₃]_ph ≈ 0.01 ÷ 0.03, [NO]₀./[O₃]_ph ≈ 30 ÷ 100. Отметим, что оба кинетических параметра хорошо согласуются с данными работ [1,3-5], а отношения [O₃]₀./[O₃]_ph и [NO]₀./[O₃]_ph близки к осредненным по стратосферному участку траектории характеристикам первичного РС. Расчеты также показывают, что физическое разбавление озоносферы не является существенным фактором снижения O₃, а уровень начального истощения озона [O₃]₀./[O₃]_ph аддитивен с обусловленным чисто химическими процессами.

Чтобы аппроксимировать результаты компьютерных экспериментов [3 - 6] уравнениями (12) пришлось включить r₀ в число подгоночных параметров. Варьирование начального размера возмущения потребовалось, чтобы учесть неодновременность воздействия РН на различные слои стратосферы: вычисленная осредненная величина r₀ ≈ 1000 м на порядок превышающая локальный начальный радиус следа.

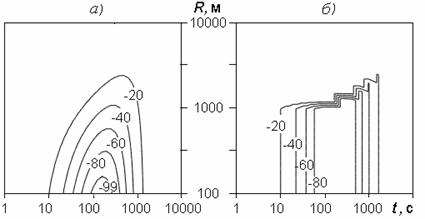
Рис. 2. Динамика интегрального возмущения стратосферного озона, инициированного единичным пуском РН «Протон»: а – детальный расчет по моделям [3-5]; б – аппроксимация согласно уравнению (7).

На рисунке R – радиус следа, м; t – время, с; интегральное возмущение озона выражено в процентах, а фоновый уровень составляет 8.5·10¹⁸ см^-2 (примерно 300 Добсонов); H – высота над уровнем моря, м

Относительное отличие численных результатов и аппроксимации (12) (см. рис. 2, фрагменты а и б) не превышает 3^1/2, что свидетельствует о простоте динамики «озоновых дыр» такого типа и, следовательно, о возможности верно оценивать их параметры и динамику предложенным здесь способом. Следует отметить, что экстенсивная характеристика выброса dm/dt (m– масса ракеты) влияет только на размер возмущенной области, а содержание разрушающего озон оксида азота – одновременно на размер r₀ и максимальный уровень возмущения [NO]₀./[O₃]_ph.

4. ЗАКЛЮЧЕНИЕ

Несмотря на достоинства предложенного упрощенного подхода, он призван дополнить, но не заменить компьютерную имитацию процесса на основе моделей высокого разрешения. Минимальная модель (7) служит лишь удобной проекцией реальных сильно нелинейных систем высокой размерности в строго очерченном интервале параметров.

Работа выполнена при поддержке РФФИ (гранты 05-08-33433-а, 07-08-12275-офи).

СПИСОК ЛИТЕРАТУРЫ

1. Экологические проблемы и риски воздействия ракетно-космической техники на окружающую природную среду. Справочное пособие / Под ред. А.В. Адушкина. М.: Анкил, 2000, 640 с.
2. Пирумов У.Г. Математическое моделирование в проблемах охраны воздушного бассейна. М.: Изд-во МАИ. 2001. 244 с.
3. Бакулин В.Н., Потопахин В.А., Яценко О.В. Модели физико-химического возмущения озоносферы, сопровождающего запуски ракет-носителей // Мат. моделирование. 2005. Т. 17. № 8. С. 81-94.
4. Яценко О.В., Ладоша Е.Н.  Космическая экология: Антропогенные воздействия на стратосферный озон при запусках жидкотопливных ракет-носителей (теоретические оценки, компьютерная имитация) // Инженерная экология. 2005. № 6. С. 27-45.
5. Яценко О.В., Ладоша Е.Н. Теоретическая оценка влияния реактивных выбросов ракет-носителей на стратосферный озон // Безопасность жизнедеятельности. 2005. № 8. С. 31-35.
6. Бакулин В.Н., Ладоша Е.Н., Потопахин В.А., Яценко О.В. Программные средства синтеза и анализа компьютерных моделей (фото)-химически активных газов для аэрокосмических исследований // Мат. моделирование. 2006. Т. 18. № 9. С. 79-91.

20 июня 2008 г.