Распознавание типа модуляции сигналов цифровых линий связи
Аннотация
Представлен метод автоматического распознавания типа фазовой и квадратурной манипуляции цифровых сигналов в условиях полной априорной неопределенности параметров сигналов.
Ключевые слова: квадратурная манипуляция, фазовая манипуляция, распознавание типа модуляции. № гос. регистрации 0420900096\001405.13.01 - Системный анализ, управление и обработка информации (по отраслям)
ФГУП «РНИИРС»
Представляемая на конкурс работа посвящена решению актуальной в области цифровой обработки сигналов проблемы – распознаванию типа модуляции сигналов цифровых линий связи. Эта проблема важна для решения задач радиомониторинга, а так же при построении адаптивных автоматически реконфигурирующихся систем связи, использующих сигналы различных типов модуляции в зависимости от качества канала и задач пользователя. К таковым, в частности, относятся беспроводные сети, т.н. 4G software radio, интеллектуальные модемы. В таких системах приемник должен автоматически определять тип модуляции входящего сигнала.
В ходе выполнения работы был разработан метод автоматического распознавания типа фазовой и квадратурной манипуляции сигналов из набора ФМ2, ФМ4, ФМ8, КАМ16, КАМ32, КАМ64, КАМ128, КАМ256 в условиях полной априорной неопределенности параметров сигналов.
Разработанный метод определения типа модуляции не требует участия оператора и основан на анализе векторной диаграммы сигнала [1].
Для построения векторной диаграммы проводим дискретизацию и фильтрацию сигнала, определение несущей и тактовой частот, восстановление сигнала в середине тактового интервала.
Формула, определяющая смещение от времени первого имеющегося отсчета до ближайшего оптимального момента взятия отсчета сигнала, может быть записана в виде:
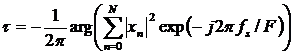 , (1)
, (1)
где ![]() - комплексные отсчеты сигнала,
- комплексные отсчеты сигнала, ![]() - тактовая частота,
- тактовая частота, ![]() - частота дискретизации. Аналогичная формула для частного случая, когда кратна , была получена в работе [2].
- частота дискретизации. Аналогичная формула для частного случая, когда кратна , была получена в работе [2].
Восстанавливаем сигнал, начиная с момента времени τ, с шагом Δ = 1/![]() . Для получения надежного результата количество восстановленных отсчетов должно быть не менее 10000.
. Для получения надежного результата количество восстановленных отсчетов должно быть не менее 10000.
Фазу несущей частоты определяем по спектру восстановленного комплексного сигнала, возведенного в четвертую степень, по формуле
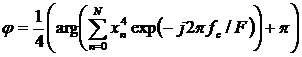 , (2)
, (2)
где ![]() - комплексные отсчеты сигнала, интерполированного в оптимальные моменты времени, -
- комплексные отсчеты сигнала, интерполированного в оптимальные моменты времени, -![]() несущая частота,
несущая частота, ![]() - частота дискретизации.
- частота дискретизации.
Найденную по формуле (2) фазу несущей компенсируем в сигнале умножением на соответствующий фазовый множитель. На рисунке 1 приведен пример векторной диаграммы для сигнала КАМ16 после выполнения тактовой и фазовой синхронизации.
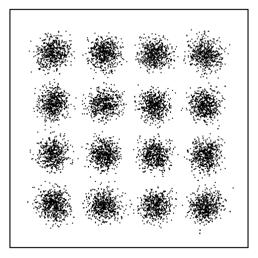
Рисунок 1. Векторная диаграмма сигнала после выполнения тактовой и фазовой синхронизации (сигнал КАМ16).
Классификация сигналов по типу шум, ФМ или КАМ осуществляется посредством анализа дисперсии амплитуды отсчетов на векторной диаграмме.
Алгоритм анализа кратности модуляции отличается для сигналов ФМ и КАМ типов.
Для случая сигналов КАМ типа воспользуемся моделью сигнала с квадратурной манипуляцией, предложенной в работе [3]. После выполнения тактовой и фазовой синхронизации отсчеты комплексного сигнала могут быть представлены в следующем виде:
![]() , (3)
, (3)
где ![]() – комплексный отсчет сигнала, соответствующий
– комплексный отсчет сигнала, соответствующий ![]() -му переданному символу,
-му переданному символу, ![]() и
и ![]() – его синфазная и квадратурные составляющие,
– его синфазная и квадратурные составляющие, ![]() и
и ![]() – амплитуда и фаза
– амплитуда и фаза ![]() -го переданного символа,
-го переданного символа, ![]() - шум, который будем считать гауссовым случайным процессом с нулевым средним и дисперсией
- шум, который будем считать гауссовым случайным процессом с нулевым средним и дисперсией ![]() .
.
Тогда плотность вероятности для отсчетов сигнала может быть записана в следующем виде:
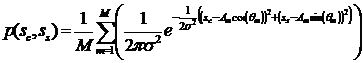 , (4)
, (4)
где![]() – число точек в сигнальном созвездии,
– число точек в сигнальном созвездии, ![]() и
и ![]() – амплитуда и фаза
– амплитуда и фаза ![]() -го узла сигнального созвездия.
-го узла сигнального созвездия.
В терминах плотности вероятности амплитуды ![]() и фазы
и фазы ![]() сигнала выражение (4) принимает вид [3]:
сигнала выражение (4) принимает вид [3]:
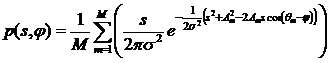 , . (5)
, . (5)
Задача распознавания типа модуляции может быть сформулирована следующим образом. Полагаем, что имеется сигнал ![]() с одним из заранее известных типов модуляции. Получаем
с одним из заранее известных типов модуляции. Получаем ![]() гипотез,
гипотез,![]() которые состоят в том, что в сигнале используется тип модуляции
которые состоят в том, что в сигнале используется тип модуляции ![]() . Функция правдоподобия для этих гипотез записывается в виде условной вероятности
. Функция правдоподобия для этих гипотез записывается в виде условной вероятности
![]() . (6)
. (6)
Стандартным подходом [3, 4] является применение теоремы Байеса. В предположении, что априорная вероятность всех гипотез ![]() одинакова, нахождение функции правдоподобия для гипотез сводится к вычислению условной вероятности наблюдаемого вектора
одинакова, нахождение функции правдоподобия для гипотез сводится к вычислению условной вероятности наблюдаемого вектора ![]() при гипотезе
при гипотезе ![]() , которая записывается в виде:
, которая записывается в виде:
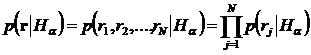 , (7)
, (7)
где ![]() - апостериорная вероятность, вычисляемая при помощи формулы (5) (см. [3]).
- апостериорная вероятность, вычисляемая при помощи формулы (5) (см. [3]).
Однако, как показали экспериментальные проверки, надежность метода распознавания, основанного на теореме Байеса, резко снижается при увеличении количества гипотез ![]() . Для преодоления этой трудности вычислим эмпирическую плотность вероятности амплитуды и фазы точек векторной диаграммы и сведём функцию правдоподобия к условной вероятности предполагаемого сигнального созвездия, соответствующего гипотезе
. Для преодоления этой трудности вычислим эмпирическую плотность вероятности амплитуды и фазы точек векторной диаграммы и сведём функцию правдоподобия к условной вероятности предполагаемого сигнального созвездия, соответствующего гипотезе ![]() , при наблюдаемом векторе
, при наблюдаемом векторе ![]() .
.
Эмпирическая плотность вероятности отсчетов сигнала может быть получена с помощью низкочастотной двумерной пространственной фильтрации с импульсной характеристикой фильтра, соответствующей теоретическому распределению отсчетов сигнала вблизи узлов сигнального созвездия. Для нашей модели сигнала она имеет вид:
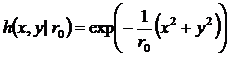 . (8)
. (8)
При этом процесс фильтрации описывается следующим уравнением:
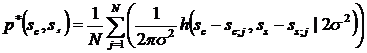 , (9)
, (9)
где ![]() и
и ![]() - синфазная и квадратурная составляющие имеющихся на векторной диаграмме отсчетов сигнала,
- синфазная и квадратурная составляющие имеющихся на векторной диаграмме отсчетов сигнала, ![]() - число отсчетов по которым проводится распознавание. На рисунке 2 приведен пример изображенной тонами серого цвета эмпирической плотности вероятности для сигнала, представленного на векторной диаграмме, изображенной на рисунке 1.
- число отсчетов по которым проводится распознавание. На рисунке 2 приведен пример изображенной тонами серого цвета эмпирической плотности вероятности для сигнала, представленного на векторной диаграмме, изображенной на рисунке 1.

Рисунок 2. Эмпирическая плотность вероятности (сигнал КАМ16).
Искомая апостериорная вероятность может быть представлена в виде
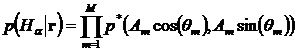 . (10)
. (10)
Для преодоления вычислительных трудностей перейдём в формуле (10) от произведения вероятностей к сумме их логарифмов, что, с учётом монотонности функции логарифма, не повлияет на процедуру принятия решения.
Аналогичным образом может быть получена и эмпирическая плотность вероятности амплитуды и фазы сигнала.
Тогда в качестве функции правдоподобия для гипотез ![]() может быть выбрана функция
может быть выбрана функция
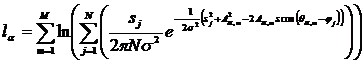 . (11)
. (11)
Для принятия решения относительно типа модуляции выбираем ту из гипотез ![]() , для которой значение функции
, для которой значение функции ![]() оказывается наибольшим.
оказывается наибольшим.
Для определения кратности модуляции сигнала ФМ типа анализируются свойства симметрии эмпирической плотности вероятности (10) для отсчетов сигнала. Используется тот факт, что сигнал ФМ2 не инвариантен к повороту на 90° относительно поворотов вокруг центра векторной диаграммы, в то время как ФМ4 и ФМ8 инвариантны; ФМ4 – не инвариантен к повороту на 45°, в сигнал ФМ8 инвариантен. Это позволяет определять кратность модуляции сигнала ФМ типа, не прибегая к фазовой синхронизации и определению уровня сигнала, а так же в случае некоторых нелинейных искажений.
В ходе внедрения полученных результатов создана программная реализация разработанного метода для автоматического (без участия оператора) определения типа модуляции. При этом вероятность правильного распознавания для разработанного метода оказывается не ниже 90% при отношении сигнал-шум не менее 5 дБ для сигналов ФМ типа, 10 дБ для КАМ16 и КАМ32, 15 дБ для КАМ64 и 19дБ для КАМ128, КАМ256. Представленный метод обладает свойством универсальности, поскольку не накладывает ограничений по кратности частоты дискретизации и тактовой частоты сигнала и применим для широкого диапазона кратностей модуляции.
Литература
1. Жуков К. Г., Махмудов А. А., Самойлик В. А. Распознавание типа квадратурной манипуляции методом максимального правдоподобия // Общие вопросы радиоэлектроники. Вып. 1. Часть 2. С. 64 – 69.
2. Oerder M., Myer H. Digital Filter and Square Timing Recovery // IEEE Transactions on communications, Vol. COM-36. No. 5. May 1988. pp. 605-612.
3. Yang Y., Chang J., Liu J., Liu C. Algorithms for QAM signal classification using maximum likelihood approach based on the joint probability densities of phases and amplitudes // Journal of C.C.I.T. Vol.32 No.1 nov. 2003.
4. Фукунага К. Введение в статистическую теорию распознавания образов. М. Наука. 1979 г.