Исследование напряжений в окрестности плоского горизонтального выреза
Аннотация
Предлагается точное решение задачи для плоского горизонтального выреза, в котором учитывается концентрация напряжений в зависимости от геометрических параметров выреза. Полученное решение позволит решать задачи, связанные с оптимальным проектированием конструкций и деталей машин с подобными технологическими элементами.
Ключевые слова: Вырез, сопряжение, задача, уравнение, решение, напряжение.Ключевые слова:
Часто детали машин и строительные конструкции имеют технологические вырезы, ослабляющие их (рис. 1). Под действием внешних нагрузок возле краев таких вырезов возникает концентрация напряжений, приводящая к возникновению трещин или больших остаточных деформаций, что является недопустимым явлением.
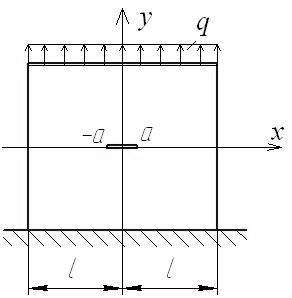
Рис. 1 Расчетная схема прямоугольной полосы с горизонтальным вырезом
Задач является актуальной проблемой прочности , так как аналитические решения, при условии их корректности и правильного задания дополнительных краевых условий, позволяют решать не только прямые, но и обратные задачи. Основные трудности в решении связаны с определением напряжений на линии сопряжения, совпадающей с осью х. Для решения этой задачи используем характеристическую часть сингулярного интегрального уравнения с постоянными коэффициентами A и B на отрезке [-a;a] [1]:
,
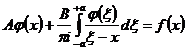где 
, u, v – перемещения точек линии сопряжения; 
;
– нормальные и касательные напряжения на линии сопряжения.
В случае неограниченного решения в узлах 
имеем:
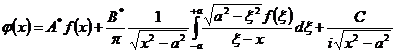, (1)
где А*, В*, С – постоянные.
Допустим, что на линии интегрирования 
перемещения принимают вид:
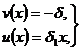
где δ, δ1 – некоторые постоянные.
Тогда
,
а выражение (1) можно переписать
,
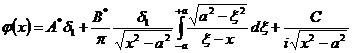из которого, разделяя действительную и мнимую части, получаем:
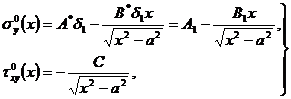
где 
, 
, – постоянные, зависящие от упругих свойств и внешней нагрузки.
Для их определения составим условия равновесия:
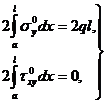
откуда
, (2)
,
и краевое условие –
. (3)
Решая совместно (2) и (3), получаем
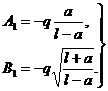
Напряжения примут вид:
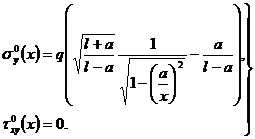
Касательные напряжения на линии сопряжения отсутствуют, следовательно, 
главное напряжение. Главное напряжение 
определим через максимальные касательных напряжений:
, (
),
.
Таким образом, имеем
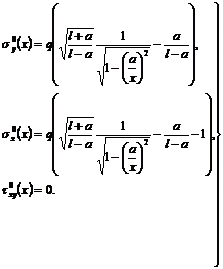(4)
Если устремить l к бесконечности, получим приближенные формулы:
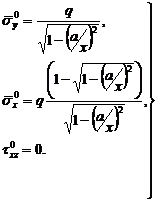(5)
Аналогично будет, если вырез рассматривать как эллиптическое отверстия с полуосями а и b, радиус b которого стремится к нулю [2]. Определим отношение l/t, при котором отклонение напряжений, найденных по выражениям (4) и (5) не превышают заданной погрешности Δ. Для этого достаточно сравнить 
и 
, откуда
.
Например, при 
- 
; при 
- 
.
Из формул (4) и (5) видно, что на концах плоского разреза напряжения стремятся к бесконечности, хотя на самом деле концы имеют радиус, который равен h (рис. 2).
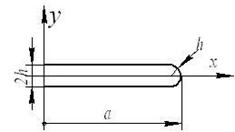
Рис. 2 Вырез с закругленными концами
Обозначим через α1 теоретический коэффициент концентрации напряжений по нормальным напряжениям 
, то есть
,
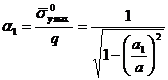где а1 – половина длины разреза с идеально острыми концами.
Пусть напряжения 
равны напряжениям на контуре эллиптического отверстия с большей полуосью 2а, при y=0. Совмещая концы контуров выреза и эллиптического отверстия (рис. 3), можно определить параметр а1
,
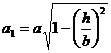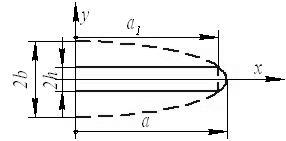
Рис. 3 Схема приведения выреза с закругленными концами к эллиптическому отверстию
. (6)
С другой стороны, согласно [2]
. (7)
Приравняв (6) и (7), получим
,
,
.
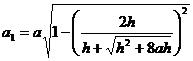Итак, для случая ограниченного решения на концах разреза выражения (4) можно переписать
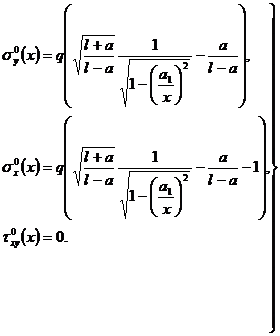(8)
Кроме радиусов закруглений концов плоского выреза, на коэффициент концентрации влияет текучесть. В этом случае следует считать
,
где σТ – предел текучести.
Доказывая решения (8) на рис. 4 показаны теоретические и экспериментальные эпюры напряжений 
в безразмерных величинах при 
, 
. Эксперименты были проведены на модели из органического стекла при помощи лазерного интерферометра по методике, описанной в [3].
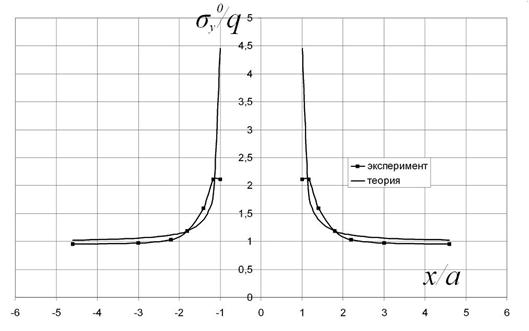
Рис. 4 Сравнение теории с экспериментом
Сравнительный анализа показал, что относительное отклонение теории от эксперимента не превышает 8% на участке 
. У концов выреза 
наблюдается существенное расхождение кривых из-за того, что в этой зоне материал пластичен, то есть эффективный (опытный) коэффициент концентрации напряжений в этой зоне должен быть равен
,
что также согласуется с теорией.
Таким образом, можно сделать вывод, что представленные аналитические решения (4) и (8) могут быть использовано для исследования концентрации напряжений возле технологических вырезов или дефектов различного рода в деталях машин.
Литература:
1.Мусхелишвили Н.И. Сингулярные интегральные уравнения. – М.: «Наука», 1968. – 512 с.
2.Демидов С.П. Теория упругости: Учебник для вузов. – М.: Высш. школа, 1979. – 432 с.
3.Беркутов В.П., Гусева Н.В., Дородов П.В., Киселев М.М. Интерферометр для определения нормальных напряжений в плоских прозрачных моделях // Датчики и системы, – №2. – 2009. – С. 26-30.