Тригональная хиральная и гексагональная двумерные квазикристаллические укладки

Аннотация

Д.С. Рошаль, С.Б. Рошаль

Рассмотрено построение двумерных укладок путём специфического проектирования трёхмерной кубической решётки. При разном  выборе области проектирования получены апериодические укладки равных ромбов, обладающие различной локальной симметрией.  Среди них – обычная апериодическая укладка, обладающая локальными элементами группы симметрии С6v и хиральная тригональная укладка, построенная аналогично хиральной пентагональной квазикристаллической решётке Пенроуза[1], реализующейся в вирусных капсидах[2].
Ключевые слова: Квазикристалл, квазикристаллическая решётка, двумерный квазикристалл, хиральный квазикристалл.

Ключевые слова:

01.04.07 - Физика конденсированного состояния

Рассмотрено построение двумерных укладок путём специфического проектирования трёхмерной кубической решётки. При разном  выборе области проектирования получены апериодические укладки равных ромбов, обладающие различной локальной симметрией.  Среди них – обычная апериодическая укладка, обладающая локальными элементами группы симметрии С_6v и хиральная тригональная укладка, построенная аналогично хиральной пентагональной квазикристаллической решётке Пенроуза[1], реализующейся в вирусных капсидах[2].

Квазикристаллы — твёрдые тела, характеризующиеся поворотной симметрией, запрещённой в классической кристаллографии и наличием дальнего порядка нетрансляционного типа. Квазикристаллы в отличие от кристаллов имеют оси пятого, восьмого, десятого и двенадцатого порядка [3-9] , и вследствие этого  не могут иметь периодической структуры. Однако организация квазикристаллической структуры похожа на кристаллическую. Квазикристаллическая структура формируется из одинаковых составляющих частей (кластеров) расположенных в узлах апериодической укладки [10], часто называемой  квазирешёткой. Кластеры в квазикристалле играют роль элементарных ячеек в кристалле. В отличие от кристаллических ячеек кластеры в квазикристаллах накладываются друг на друга, но число типов различных наложений ограничено. В кристаллической решетке число элементарных трансляций равно размерности пространства, в котором существует кристалл. В известных квазирешетках это число удвоено: все планарные квазирешетки можно спроектировать из 4-мерного пространства, а объемные – из шестимерного. Поэтому трансляции квазирешетки являются  проекциями  трансляций обычной периодической, но многомерной решетки.
Математические методы проектирования из многомерного пространства хорошо разработаны [11], однако представить себе многомерные объекты весьма сложно, особенно на начальной стадии изучения кристаллографии квазикристаллов.  Цель настоящей работы – сделать объекты многомерной кристаллографии доступнее,  рассмотрев различные методы проектирования простой трёхмерной кубической решётки, приводящие  к двумерным квазирешеткам разной симметрии.  
Рассмотрим принципы построения квазирешётки на самой простой модели квазикристалла – одномерной [12]. В такой модели одномерный квазикристалл проектируется из плоской  квадратной решётки с периодом a=1.  При этом на одномерное пространство E^|| проектируются только те узлы квадратной решетки, которые попадают в область проектирования(ОП) - полосу, лежащую между двумя параллельными прямыми (см. рис. 1). Если выбрать ширину полосы проектирования h равной проекции одной ячейки квадратной решетки на направление, перпендикулярное к полосе:
,    (1)
где   - угол между горизонталью и полосой проектирования, то вершины, попавшие в полосу, после проектирования на проективную прямую E|| разбивают её на короткие S и длинные L отрезки. Длина этих отрезков, а также их чередование, зависят от  наклона полосы. Заметим, что канонические квазикристаллические укладки тоже образуются двумя типами структурных элементов, а ширина ОП также определяется размерами элементарной ячейки многомерного пространства в соответствующем направлении.

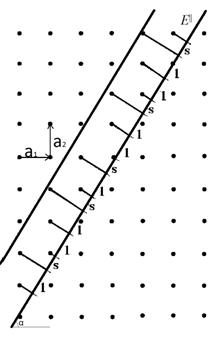
Рис. 1. Проектирование одномерной квазикристаллической решётки.

В рассматриваемой модели координата любого  узла квазирешетки r представима в виде целочисленной линейной комбинации двух базисных трансляций:
,    (2)
где n_i  - целые,  и  - проекции базисных трансляций a₁  и  a₂ на направления E^||. Перпендикулярная координата узла есть
,  (3)
где переменная v- фазонная степень свободы [13,14], определяющая сдвиг линии E^||  относительно первоначальной системы координат.  Величины a1┴, a2┴- проекции базисных трансляций на E┴. Трансляции квадратной решетки в базисе (E^||, E┴) имеют вид:  и  . Несложно убедиться в том, что узел принадлежит укладке, если . Данная модель квазикристаллической решетки обладает теми же особенностями, что и квазикристаллические решетки, получаемые путем проектирования многомерных пространств. Во-первых, координаты любого узла решетки можно представить в виде целочисленной линейной комбинации двух базисных трансляций, а во-вторых, разбиение пространства осуществляется двумя типами структурных элементов.                     
Теперь, используя описанные выше принципы построения квазикристаллической укладки, рассмотрим более сложную и неисследованную в литературе ранее двумерную квазикристаллическую укладку, проектируемую из трёхмерного пространства.  Узлы укладки представляют собой проекции узлов простой кубической решётки, а рёбра укладки являются проекциями ее минимальных трансляций. Проектирование в предлагаемой модели ведется вдоль направления (1,1,1). Поэтому координаты узла данной гексагональной укладки можно записать в виде
,   (4)
Для начала рассмотрим случай, когда ОП является полосой между двумя параллельными плоскостями   с вектором нормали (m,p,q) близким к направлению (1,1,1). Поэтому перпендикулярная координата узла равна
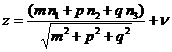,   (5)
где v- фазонная степень свободы укладки. Расстояние между плоскостями  определяется величиной проекции элементарной кубической ячейки на направление (m,p,q). Соответственно узел принадлежит укладке, если 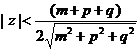. В рассматриваемом нами случае перпендикуляр к полосе немного отличается от направления (1,1,1), соответственно ширина полосы немного отлична от. При любых малых углах отклонения полосы получается бездефектная апериодическая укладка 60° ромбов, похожая на показанную на рисунке 2.

Рис.2 Двумерная квазикристаллическая решётка, полученная путём проектирования трёхмерной простой кубической решётки.

Так как нормаль к полосе проектирования немного отличается от направления (1, 1,1), то глобальные элементы симметрии превращаются в локальные. Оси шестого порядка укладки возникают из зеркально-поворотных осей кубической решётки. Области с локальной симметрией С_6v включают в себя не менее двенадцати ромбов. Центры данных областей расположены апериодическим образом и отмечены на рисунке 2 заполненными кружками. В случае (m,p,q) =(1,1,1) апериодическая укладка превращается в обычную периодическую гексагональную укладку 600 ромбов.
Перейдем теперь к рассмотрению укладок, соответствующих неплоской ОП.  Рассмотрим простейший нелинейный   случай расположения ОП между двумя эллиптическими параболоидами:
 и  .  (6)
Параболоиды заданы в системе координат (4-5) и сдвинуты друг относительно друга вдоль  направления  (m,p,q) =(1,1,1) на величину h =,  снова равную проекции кубической ячейки на  данное направление. Как и ранее, данный выбор ширины полосы h делает укладку бездефектной,  если коэффициент нелинейности α мал.  

Рис.3. Двумерная укладка с глобальной симметрией С_3v.

Выбранная ОП инвариантна относительно группы симметрии С_∞v. Поэтому согласно известному принципу Кюри [15] укладка, представленная на Рис. 3, имеет только глобальные элементы симметрии, общие для ОП и кубической решетки. Это одна ось третьего порядка и три плоскости симметрии, проходящие через данную ось.
За счет нелинейной фазонной деформации можно получить и хиральные квазикристаллические укладки, то есть укладки, не имеющие плоскостей симметрии. Как известно, хиральные объекты могут иметь уникальные свойства, широко применяемые в химии, биологии и физике. Для  построения хиральной тригональной укладки мы воспользуемся  методом, аналогичным методу построения хиральной пентагональной квазикристаллической решётки Пенроуза [1], реализующейся в вирусных капсидах [2].Чтобы убрать плоскости симметрии из квазикристаллической укладки, нам нужно изменить полосу проектирования так, чтобы либо она имела только ось симметрии третьего порядка, но не имела плоскостей симметрии, либо чтобы плоскости симметрии ОП не совпадали с плоскостями симметрии кубической решётки. Ниже мы остановимся на втором варианте, так как его  “нелинейность” меньше.  Для получения хиральной укладки удобно воспользоваться ОП, описанной ранее, но прогофрировать параболоиды вдоль направления (1,1,1). С этой целью мы перенормируем константу  в  (6) и положим ,  где φ – азимутальный  угол в плоскости (4), а константа φ₀ определяет угол между плоскостями симметрии кубической решетки и плоскостями симметрии гофрированных параболоидов. Укладка, полученная по данному алгоритму, представлена на рис. 4.

Рис.4. Хиральная укладка с глобальной симметрией С₃.

Таким образом, при проектировании квазикристаллической структуры из  пространства большей размерности можно сохранить или уничтожить глобальные элементы симметрии пространства большей размерности за счет  выбора различных по форме ОП. Бездефектности квазикристаллической укладки можно добиться за счёт подходящего выбора ширины ОП. Разработанным в работе методом получены  апериодическая укладка, обладающая симметрией С6v , укладка, обладающая глобальной осью третьего порядка и тремя глобальными плоскостями симметрии и хиральная укладка.
Литература:
1.Penrose R. The role aesthetics in pure and applied mathematical research //J. Inst. Math. Its Appl. - 1974.-Vol. 10.-P. 266.
2.Konevtsova, O.V., Rochal, S.B. & Lorman, V.L. Chiral Quasicrystalline Order and Dodecahedral Geometry in Exceptional Families of Viruses //Phys. Rev. Lett. - 2012.-Vol. 108.-P. 038102.
3.Wang N., Chen H., Kuo K.H.Two-dimensional quasicrystal with eightfold
rotational symmetry // Phys. Rev. Lett. - 1987. - Vol. 59. - P. 1010 - 1013.
4.Bendersky L. Quasicrystal with one-dimensional translational symmetry and a tenfold rotation axis //Phys. Rev. Lett.-1985.-Vol. 55.-P. 1461-1463.
5.Bendersky L. Decagonal phase //J. de Physique C3.-1986.-Vol. 47.-P. 457-461.
6.Fung K.K., Yang C.Y., Zhou Y.Q., Zhao J.G., Zhan W.S., Shen B.G.
Icosahedrally Related Decagonal Quasicrystal in Rapidly Cooled Al-Fe Alloy //Phys. Rev. Lett.- 1986.-Vol.-56.-P. 2060-2063.
7.Daulton   T.L., Kelton K.F. The decagonal phase in (Al,Si)65Co2oCu15 alloys //Phil. Mag. B.-1992.-Vol. 66.-P. 37-61.
8.Ishimasa T., Nissen H.U., Fukano Y. New ordered state between crystalline and amorphous in Ni-Cr particles //Phys. Rev. Lett.-1985.-Vol. 55.-P. 511-513.
9.Chen H., Li D., Kuo K.H. New type of two-dimensional quasicrystal with twelvefold rotation symmetry //Phys. Rev. Lett.- 1988.-Vol 60.-P. 1645-1648.
10.Burkov S.E.Structure Model of the Al-Cu-Co Decagonal Quasicrystal //Phys. Rev. Lett.- 1991.-Vol. 67.-P. 614-617.
11.Wolff  P.M. The Pseudo – Symmetry of modulated Crystal Structures // Acta Cryst. A. – 1974.- Vol. 30. – P. 777-785.
12.Самоподобие, порождаемое проекциями //Сайт симметрия URL: http://zventa.pp.ua/samopodobie-porozhdaemoe-proekciyami-2 (дата обращения: 12.05.2012).
13.Lubensky T.C., Socolar J.E.S., Steinhardt P.J., Bancel P.A., Heiney P.A. Distortion and peak broadening in| quasicrystal diffraction patterns //Phys. Rev.Lett.-1986.-Vol. 57.-P. 1440-1443.
14.Socolar J.E.S. Simple octagonal and dodecagonal quasicrystals //Phys. Rev. B.- 1989,-Vol. 39.- P. 10519-10551.
15.Шаскольская М.П. Кристаллография: Учеб. Пособие для втузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1984. – 376 с.