Оптимизационный метод статического расчета строительных конструкций с применением вероятностных законов с ограничениями
Аннотация
Дата поступления статьи: 30.04.2013Рассматривается анализ применения метода Н.С. Стрелецкого для статического расчета строительных конструкций. Предлагается на основе вероятностно-статистического метода Н.С. Стрелецкого вместо нормальных законов для действующих напряжений и прочности применять законы со сдвигом, в частности, закон Вейбулла с тремя параметрами и Фишера-Типпета. Предлагается выполнить переход к параметрам совокупности конечного объема, что позволит повысить точность расчета вероятности безотказной работы и предлагаемого вероятностного запаса прочности, а также оптимизировать величину вероятности безотказной работы строительных конструкций
Ключевые слова: оптимизация, расчет, конструкции, сталь, выборка, вейбулл, фишер-типпет
В 40-х годах XX века советский ученый, чл.-корр. АН СССР Н.С. Стрелецкий [1] внес предложение перейти от метода расчета строительных конструкций по допускаемым напряжениям к вероятностно-статистическому методу.
Величина вероятности отказа в случае нормального закона (по методу Н.С. Стрелецкого) определяется по формуле (1):
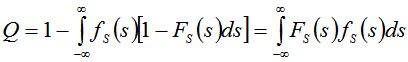 . (1)
. (1)
Усовершенствовать метод Н.С. Стрелецкого и более точно определять вероятность безотказной работы строительных конструкций возможно, если вместо нормального закона применять законы со сдвигом, например, закон Вейбулла с тремя параметрами, имеющий одним из параметров – сдвиг кривой плотности распределения.
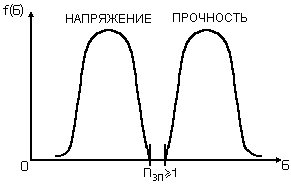
Рис. 1. – Плотности распределений Вейбулла с тремя параметрами для действующих напряжений и прочности
 - запас прочности по экстремальным значениям напряжения и прочности
- запас прочности по экстремальным значениям напряжения и прочности
Применение закона Вейбулла с тремя параметрами для действующих напряжений и несущей способности, полученные по выборочным данным, представлены на рис.1. В случае определения параметра сдвига (максимального значения) для действующих напряжений можно использовать закон Вейбулла [2]:
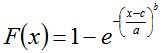 , (2)
, (2)
при этом значения вариационного ряда следует умножать на (-1).
Также возможно применение распределения Фишера-Типпета [3,4]:
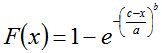 . (3)
. (3)
Для применения законов Вейбулла (2) или Фишера-Типпета (3) имеется физическое обоснование, состоящее в том, что не может быть нулевой или близкой к ней прочности конструкции (иначе разрушение происходило бы от собственного веса). В случае, когда рассматриваем действующие напряжения, а именно ограничение по максимальной величине напряжений или сдвиг распределения справа – для них обусловлены ограничения размеров конструкции природными нагрузками (ветер, снег, гололед и т.п.). Действующие факторы должны задаваться их вероятностью распределения.
Если представить на одном графике вероятность распределения для действующих напряжений и несущей способности для генеральных совокупностей конечного объема (далее совокупностей) [5], то этот график примет вид (рис.2).
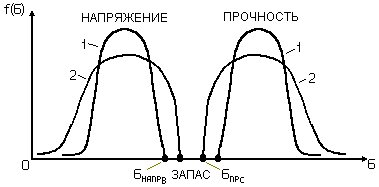
Рис. 2. – Распределение напряжения и прочности:
1 – выборки; 2 – совокупности
Для обеспечения безаварийной работы конструкции предлагается неравенство:
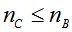 ,
,
где 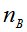 - вероятностный запас прочности по выборочным данным напряжения и прочности
- вероятностный запас прочности по выборочным данным напряжения и прочности 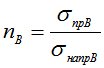 ;
;
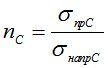 - вероятностный запас прочности по совокупностям конечного объема.
- вероятностный запас прочности по совокупностям конечного объема.
Вероятностный запас прочности для совокупности 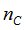 можно принять по аналогии с расчетом по предельным состояниям
можно принять по аналогии с расчетом по предельным состояниям 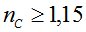 [6,7].
[6,7].
Для случая 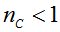 пересечение кривых распределения для совокупностей приведет к появлению величины вероятности отказа Q или вероятности безотказной работы P=1-Q.
пересечение кривых распределения для совокупностей приведет к появлению величины вероятности отказа Q или вероятности безотказной работы P=1-Q.
Тогда возникает необходимость оптимизации вероятности безотказной работы P (рис.3). Из рис.3 видно, что кривая 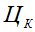 растет с увеличением P, а затраты в эксплуатации, связанные с отказами строительных конструкций снижаются. Суммарные затраты
растет с увеличением P, а затраты в эксплуатации, связанные с отказами строительных конструкций снижаются. Суммарные затраты 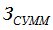 получаются сложением ординат для
получаются сложением ординат для 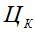 и
и 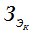 ; в итоге кривая
; в итоге кривая 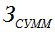 будет иметь вогнутость, а минимум
будет иметь вогнутость, а минимум 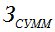 будет соответствовать
будет соответствовать 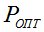 .
.
Для строительных конструкций рассмотрим случай 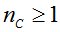 .
.
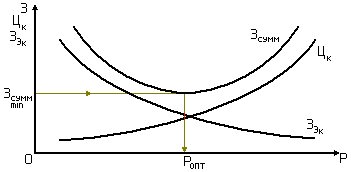
Рис. 3. – Оптимизация вероятности безотказной работы Р:
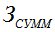 - критерий оптимизации Р;
- критерий оптимизации Р; 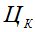 - цена конструкции;
- цена конструкции;
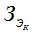 - затраты на эксплуатацию конструкции.
- затраты на эксплуатацию конструкции.
При пересечении левой и правой ветвей плотностей распределения напряжения и прочности рассматривается левая часть графика на рис.4.
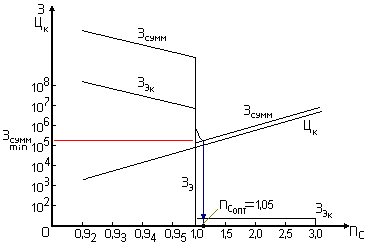
Рис. 4. – Оптимизация вероятности безотказной работы Р
и вероятностного запаса прочности для строительных конструкций
Кривая эксплуатационных затрат в этой части располагается существенно выше, для чего используется логарифмическая шкала. В правой части графика, начиная с 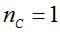 суммарные затраты
суммарные затраты 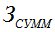 имеют точку минимума, лишь на 5% превышая
имеют точку минимума, лишь на 5% превышая 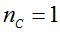 (эти 5% учитывают точность приборов и инженерных расчетов), т.е.
(эти 5% учитывают точность приборов и инженерных расчетов), т.е. 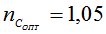 .
.
В данном случае эксплуатационные затраты не учитывают отказы строительных конструкций, а включают в себя лишь затраты на обслуживание (осмотр, окраска и т.д.).
Изложенный метод статического расчета несущей способности строительных конструкций в вероятностном аспекте с применением закона Вейбулла с тремя параметрами с ограничениями (сдвиг распределения слева для несущей способности, справа для действующих напряжений) и с переходом от выборки к совокупности [8-10] позволяет повысить точность расчета вероятности безотказной работы и вероятностного запаса прочности, а также оптимизировать величину вероятности безотказной работы строительных конструкций.
Литература
-
Стрелецкий Н.С. Основы статистического учета коэффициента запаса прочности сооружений [Текст]. – М.: Стройиздат, 1947. – 92 с.
-
Вейбулл В. Усталостные испытания и анализ их результатов [Текст]: Пер. с англ. – М.: Машиностроение, 1964. – 275 с.
-
Fisher R.A. The design of experiments [Текст], Edinburg, Oliver and Boyd. 1935.
-
Tippet. The Methods of statistics [Текст], J.,Wiley, N.J.
-
Касьянов В.Е., Зайцева М.М., Котесов А.А. Оценка параметров распределения Вейбулла для совокупности конечного объема [Текст] // Деп. в ВИНИТИ, 24.01.2012 №21-В2012.
-
Райзер В.Д. Теория надежности в строительном проектировании [Текст]. – М.: Изд-во АСВ, 1998. – 304 с.
-
Болотин В.В. Статистические методы в строительной механике [Текст]. – М.: Изд-во литературы по строительству, 1965. – 279 с.
-
Касьянов В.Е., Котесов А.А., Котесова А.А. Аналитическое определение параметров закона Вейбулла для генеральной совокупности конечного объема по выборочным данным прочности стали [Электронный ресурс] // «Инженерный вестник Дона», 2012, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2012/804 (доступ свободный) – Загл. с экрана. – Яз. рус.
-
Демченко Д.Б., Касьянов В.Е. Анализ метода статического расчета строительных стальных конструкций с применением вероятностных законов [Текст] // «Научное обозрение», 2013. – №2. – С. 97-99
-
Касьянов В.Е., Щулькин Л.П., Котесова А.А., Котова С.В. Алгоритм определения параметров прочности, нагруженности и ресурса с помощью аналитического перехода от выборочных данных к данным совокупности [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1236 (доступ свободный) – Загл. с экрана. – Яз. рус.