Нагружение блока составной конструкции из шестиугольной пластины и круговой цилиндрической оболочки
Аннотация
Дата поступления статьи: 30.04.2013Статья посвящена прочностным расчетам составных конструкций. Рассмотрена работа внешних сил, действующих на конструкцию, состоящей из основания в форме шестиугольной пластины, жестко связанной с основанием круговой цилиндрической оболочки.
Ключевые слова: пластина, оболочка, прочность, составная конструкция.
Для определения разрешающей системы уравнений для напряженно-деформированного состояния конструкции, состоящей из основания в форме шестиугольной пластины, жестко связанной с основанием круговой цилиндрической оболочки, нужно найти работу внешних сил [1]-[10].
Для того, чтобы применить принцип минимума энергии необходимо найти работу внешних сил, которая определяется как произведение перемещения на величину действующей активной силы. При подсчете величины работы силы, приложенной к кольцу, нужно учитывать толщину кольца. Рассмотрим силу, действующую на кольцо в точке В (рис. 1).
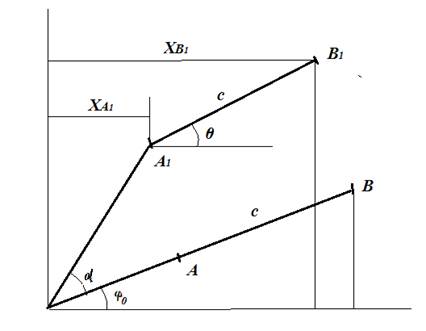
Рис. 1. – Схема для определения перемещений в точке В для кольца.
Пусть точка А приложена на том же самом радиуса, что и точка В, и при этом принадлежит как телу I, так и телу II. Если длина отрезка АВ равна с, то после деформации этот отрезок перейдет в А1В1 также равный с.
Для определения нового положения точки В после деформации необходимо определить угол θ с осью х отрезка А1В1.
Координаты точки А1 равны
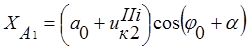 ;
; 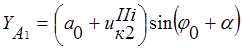 ; (1)
; (1)
Определим главные значения приращения координаты точки А после деформации:
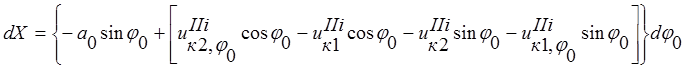 ;
;
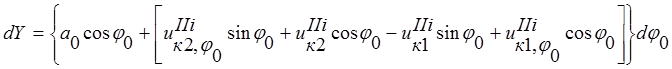 . (2)
. (2)
Введем следующие обозначения:
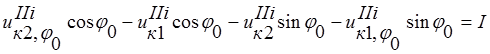 ;
;
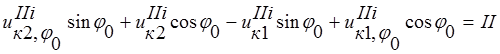 . (3)
. (3)
Таким образом, формулы (2) с учетом (3) имеют вид:
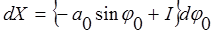 ;
; 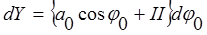 . (4)
. (4)
Очевидно, что 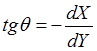 . (5)
. (5)
Подставляя (4) в (5), получим:
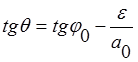 , где
, где 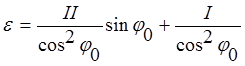 . (6)
. (6)
Используя формулы тригонометрии, можно определить:
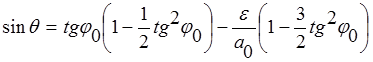 ;
; 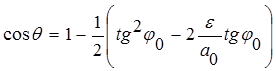 . (7)
. (7)
Координаты точки В1 после деформации равны
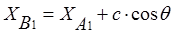 ;
; 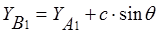 ;
; 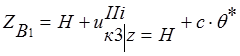 , (8)
, (8)
где 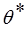 – угол поворота поперечного сечения кольца.
– угол поворота поперечного сечения кольца.
Координаты точки В после деформации равны
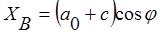 ;
; 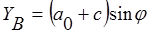 ;
; 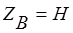 . (9)
. (9)
Учитывая (8) и (9), определим перемещения точки В:
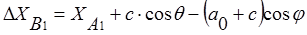 ;
;  ;
;
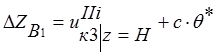 . (10)
. (10)
В формуле (10) введем обозначения:
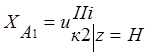 ;
; 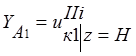 ;
; 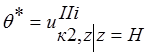 . (11)
. (11)
Учитывая (11) и 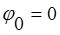 , перемещения точки В примут вид:
, перемещения точки В примут вид:
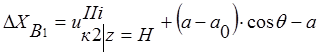 ;
; 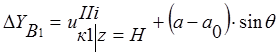 ;
;
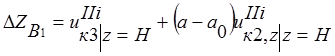 . (12)
. (12)
Определим работу внешней нагрузки на узлы кольца (рис. 2):
1). при симметричном нагружении узла кольца В1 –
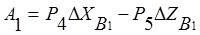 ; (13)
; (13)
2). при несимметричном нагружении узла кольца В1 –
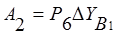 ; (14)
; (14)
Работу внешней силы в случае воздействия ее на узел тела А1 записать легко, так как все перемещения пластинки известны:
1). при симметричном нагружении узла кольца А1 –
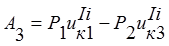 ; (15)
; (15)
2). при несимметричном нагружении узла кольца А1 –
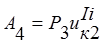 ; (16)
; (16)
| а). | 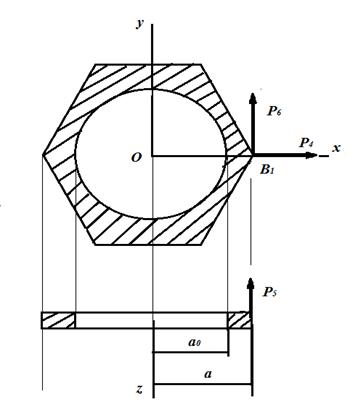 |
б). | 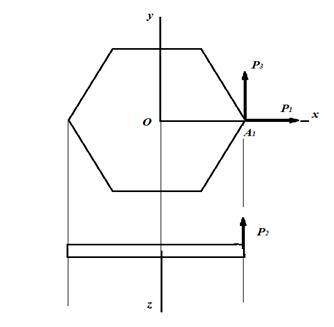 |
|
Рис. 2. – Схема нагружения для кольца. а – узла В1; б – узла А1. |
|||
Таким образом, получены все выражения для работ активных сил.
Литература
1. Краснобаев И.А., Маяцкая И.А. Основы расчета на изгиб тонких жестких пластин [Текст]: Монография / Краснобаев И.А., Маяцкая И.А. – Ростов н/Д, РГСУ, 2011.– 87 с.
2. Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. Теория пластин и оболочек: [Текст]: Монография / Краснобаев И.А., Маяцкая И.А., Смирнов И.И., Языев Б.М. – Ростов н/Д, РГСУ, 2011.– 114 с.
3. Амосов А.А. Техническая теория тонких упругих оболочек: [Текст]: Монография / Амосов А.А.–М.:АСВ, 2009, – 332 с.
4. Филин А.П. Элементы теории оболочек.–Л.:Стройиздат, 1975, – 256 с.
5. Огибалов П.М., Колтунов М.Л. Оболочки и пластины.–М.:МГУ, 1969, – 696 с.
6. Calladine C.R. Theory of shell structures.– N.Y.: Cambridge University Press, 1989, –788 p.
7. Zingoni A. Shell structures in civil and mechanical engineering.– N.Y.: Thomas Telford Publishing, 1997, –351 p.
8.Литвинов В.В., Кулинич И.И. Соотношения между компонентами поверхностной нагрузки в оболочках вращения при безмоментном их состоянии.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.
9.Стрельников Г.П., Бурцева С.В., Авилкин В.И. К расчету оболочек вариационно-энергетическим методом.[Текст] //Интернет-журнал «Инженерный вестник Дона». 2012 №4 (2) [Электронный ресурс].-М. 2012. – Режим доступа: http://www.ivdon.ru.
10. Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки.–М.:Наука, 1966, – 636 с.