К определению перемещений оболочек вариационно-энергетическим методом
Аннотация
Дата поступления статьи: 21.06.2013В статье получено в матричном виде выражение для определения неизвестных коэффицентов двойных рядов, аппоксимирующих перемещения произвольной точки срединной поверхности оболочки, которое используется при расчете оболочек вариационно-энергетическим методом .
Ключевые слова: оболочка, вариационно-энергетический метод,минимума полной потенциальной энергии системы, перемещения, деформации.
Расчет оболочек вариационно-энергетическим методом основан на принципе минимума полной потенциальной энергии системы (Э), численно равной разности работы внутренних сил (А) и внешних сил (Авн). Задача решается в перемещениях. Компоненты перемещения произвольной точки срединной поверхности оболочки ![]() вдоль осей криволинейной системы координат выбираются в виде бесконечных двойных рядов, члены которых состоят из произведения постоянных параметров
вдоль осей криволинейной системы координат выбираются в виде бесконечных двойных рядов, члены которых состоят из произведения постоянных параметров ![]() , подлежащих определению и линейно независимых функций
, подлежащих определению и линейно независимых функций ![]() , удовлетворяющих геометрическим граничным условиям
, удовлетворяющих геометрическим граничным условиям
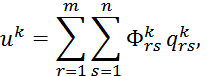
В статье [10] приводится выражение для работы внутренних сил в матричном виде в криволинейной ортогональной системе координат
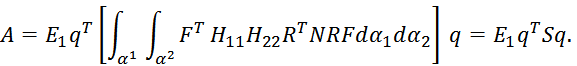
Матрица F , содержащая аппроксимирующие функции ![]() , матрицы R, N , зависящие от геометрии срединной поверхности оболочки, её толщины и материала приводятся в [10]. Матрица R, кроме коэффициентов первой и второй квадратичных форм, содержит символы Кристоффеля второго рода
, матрицы R, N , зависящие от геометрии срединной поверхности оболочки, её толщины и материала приводятся в [10]. Матрица R, кроме коэффициентов первой и второй квадратичных форм, содержит символы Кристоффеля второго рода
![]() В случае ортогональной системы координат они могут быть выражены через параметры Ляме следующим образом:
В случае ортогональной системы координат они могут быть выражены через параметры Ляме следующим образом:
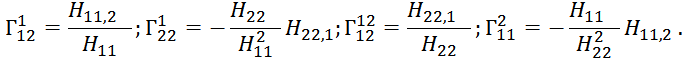
Здесь ![]() и
и ![]() производные параметров Ляме соответственно по первой и второй координатам. После подстановки символов Кристоффеля матрица R будет иметь вид:
производные параметров Ляме соответственно по первой и второй координатам. После подстановки символов Кристоффеля матрица R будет иметь вид:
| R= | |||||||||||
| 0
|
R12
|
R13
|
R14
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| R21
|
0
|
0
|
0
|
R25
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 0
|
R32
|
0
|
0
|
0
|
0
|
R37
|
0
|
0
|
0
|
0
|
0
|
| R41
|
0
|
R43
|
0
|
0
|
0
|
0
|
R48
|
0
|
0
|
0
|
0
|
| R51
|
R52
|
0
|
R54
|
0
|
R56
|
0
|
0
|
R59
|
0
|
0
|
R512
|
| R61
|
R62
|
0
|
0
|
R65
|
R66
|
R67
|
0
|
R69
|
0
|
0
|
R612
|
| R71
|
R72
|
0
|
0
|
R75
|
R76
|
R77
|
0
|
R79
|
0
|
0
|
R712
|
| R81
|
R82
|
0
|
0
|
0
|
R86
|
0
|
R88
|
R89
|
0
|
0
|
R812
|
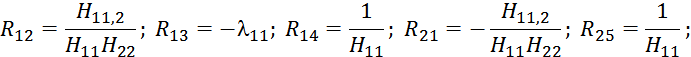
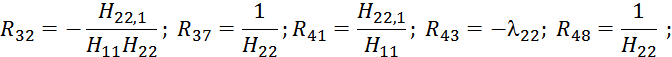
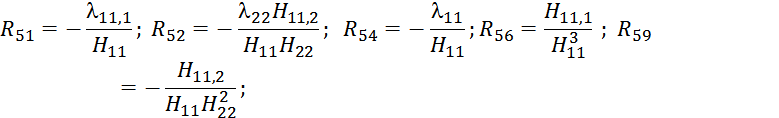
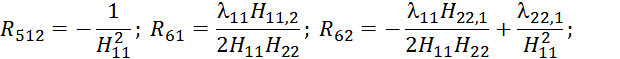
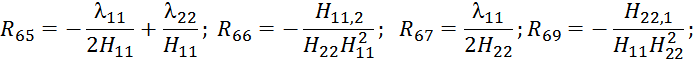
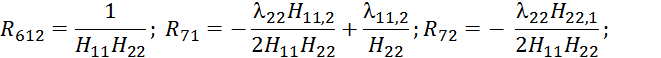
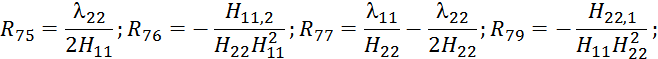
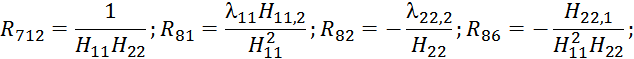
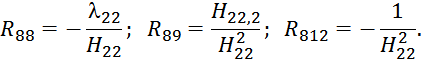
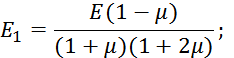
![]() ;
; ![]() .
. ![]() .
.
Матрица
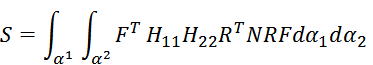 является блочной симметричной матрицей порядка 3mn × 3mn
является блочной симметричной матрицей порядка 3mn × 3mn
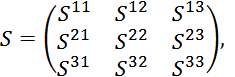 где
где
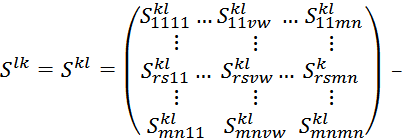 матрица порядка mn × mn
матрица порядка mn × mn
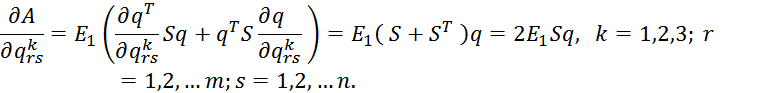
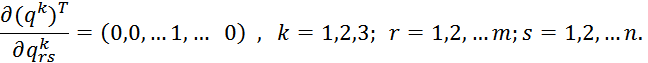
Все элементы этой матрицы будут равны нулю, кроме rs–того элемента, равного единице.
Так как матрица S симметричная, то ![]()
Выражение для работы внешних сил имеет вид
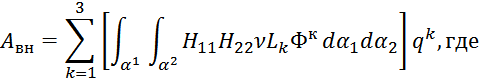
![]()
![]() проекция вектора интенсивности внешней нагрузки на оси прямоугольной декартовой системы координат.
проекция вектора интенсивности внешней нагрузки на оси прямоугольной декартовой системы координат.
![]() - матрица, содержащая косинусы углов между осями прямоугольной декартовой системы координат и векторами криволинейной системы координат, связанной со срединной поверхностью оболочки.
- матрица, содержащая косинусы углов между осями прямоугольной декартовой системы координат и векторами криволинейной системы координат, связанной со срединной поверхностью оболочки.
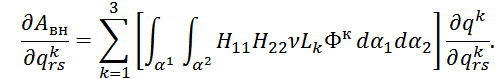 Так как только один элемент матрицы
Так как только один элемент матрицы ![]() будет равен единице, а остальные нулю, то
будет равен единице, а остальные нулю, то
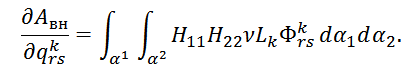
Если распределенная нагрузка действует вдоль оси x3 прямоугольной декартовой системы координат ( собственный вес конструкции ), тогда вектор ![]() и
и
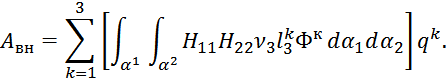
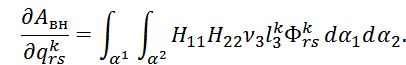
В случае нагрузки интенсивности p, направленной по нормали к срединной поверхности оболочки, матрица ![]() приобретает вид
приобретает вид
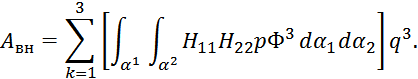
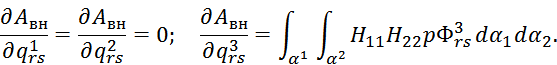
Введем матрицу
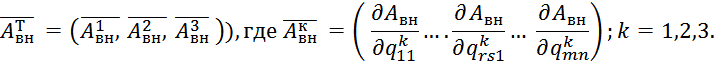 Из условия стационарности полной потенциальной энергии системы
Из условия стационарности полной потенциальной энергии системы
Э=А - Авн , получаем 3mn линейных уравнений для определения 3mn неизвестных коэффициентов ![]() .
.
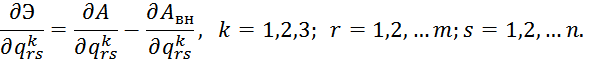
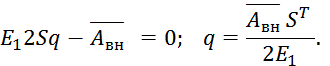
Литература:
1.Аксентян К.Б., Гордеев-Гавриков В.К. Энергетический метод расчета оболочек усложненной формы [Текст]: Монография / К.Б. Аксентян. – Ростов: РИСИ, 1976г. – 320 с.
2. Гольденвейзер А.Л. Теория упругих тонких оболочек [Текст]: Монография / А.Л. Гольденвейзер.− М. «Наука» ,1976г. – 512 с.
3. Васидзу К. Вариационные методы в теории упругости и пластичности [Текст]: Монография / Васидзу К.– М. «Мир», 1987г. – 542 с.
4. Кильчевский А.Л. Элементы тензорного исчисления и его приложение к механике [Текст]: Монография / А.Л. Кильчевский – М. ГИТТЛ, 1954г.–168с.
5.Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки [Текст]: Монография / С.П. Тимошенко. – М. «Наука», 1966г. – 636 с.
6.Филин А. В. Элементы теории оболочек. Изд. второе, дополн. и перераб. [Текст]: Монография / А. В. Филин − Л.: Стройиздат, 1975г. – 256 с.
7. Koiter W.T. A consistent first approximation in the general theory of thin elastic shells. –In: Proceedings of the Symposium on the Theory of Thin Elastic Shells, IUTAM, Delft. –Amsterdam: North-Holland, 1960, p. 12-33.
8. Reissner E. Variational considerations for elastic beams and shells. – Journal of the Engineering Mechanics Division, Proceedings of the American Society of Civil Engineers, 1962, v.88, No.EMI, p. 23-57.
9. Литвинов В.В., Языев Б.М. Энергетический метод в форме Тимошенко-Ритца для определения критических сил осевого сжатия круговой цилиндрической оболочки. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2012/722/ (доступ свободный). – Загл. с экрана. – Яз. рус.
10. Бурцева С.В., Стрельников Г.П., Авилкин В.И. К расчету оболочек вариационно-энергетическим методом. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4(2). – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1291 (доступ свободный). – Загл. с экрана. – Яз. рус.