Синтез тормозных квазиполей препятствий для бортовой системы автономного планирования траектории движения малогабаритных мобильных роботов
Аннотация
Дата поступления статьи: 26.05.2014В статье рассматривается способ синтеза тормозных регрессивных квазиполей препятствий для бортовой системы планирования траектории движения малогабаритных мобильных роботов, алгоритмическим базисом которой является бионический метод адаптивного управления интеллектуальными роботами. Тормозные регрессивные квазиполя используются для оптимизации синтезируемой траектории по критерию безопасности.
Ключевые слова: робототехника, малогабаритные роботизированные платформы, локальная навигhttp://www.ivdon.ru/admin/articlesация, планирование траектории, оптимизация траектории
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
В настоящее время решение задачи перемещения в заданную целевую локацию для большинства существующих образцов малогабаритных мобильных роботизированных платформ (ММРП) осуществляется оператором в режиме телеуправления. В то же время, существующие тенденции к повышению автономности ММРП, функционирующих в различных средах [1 - 3], определяют актуальность разработки бортовых систем, решающих данную задачу в автономном режиме.
В качестве базиса автономных режимов решения задачи перемещения в заданную целевую локацию могут служить алгоритмы, построенные на основе различных методов автоматического планирования локальных траекторий [4 - 6]. Однако при выборе одного из таких методов необходимо учитывать то обстоятельство, что автономное планирование траекторий движения для ММРП должно обеспечивать повышенную проходимость в условиях внешней среды, характерных для внутренних помещений и объектов с затрудненным доступом для человека: наличие узких проездов в целевую локацию, большое количество объектов со сложной геометрией. При этом обязательным условием является одновременное удовлетворение критериям оптимальности (минимизация энергетических затрат) и безопасности (отсутствие столкновений с препятствиями) траектории.
В работах [7, 8] показано, что данным требованиям может удовлетворять бионический метод адаптивного управления интеллектуальными роботами [9]. Суть этого метода состоит в том, что дискретный план внешней среды перед каждым элементарным действием воспроизводится в системе управления робота, после чего на нем отыскивается градиент функционала, определяемого множеством возможных траекторий движения к цели. После этого формируется и отрабатывается вектор элементарного перемещения в среде, направленный вдоль вектора антиградиента функционала, найденного на плане среды в системе управления робота.
Основное достоинство данного метода автоматического планирования локальных траекторий состоит в том, что он позволяет управлять интеллектуальными роботами не только в стационарной, но и в динамически изменяющейся, априори неформализованной внешней среде. Причем планирование оптимальных с точки зрения трудности реализации траекторий осуществляется этим методом с учетом особенностей рельефа местности. При этом данный метод может быть эффективно реализован в базисе программируемой логики [7], что особенно актуально для малогабаритных ММРП, имеющих ограниченную производительность бортовых вычислительных ресурсов. Отыскание градиента функционала, определяемого множеством возможных траекторий движения к цели, в этом случае осуществляется посредством воспроизведения параллельной итерационной процедуры распространения волн возбуждения в матрице ключевых элементов (см. рис. 1).
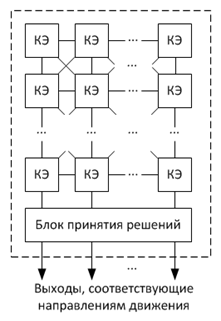
Рис. 1. – Структура матрицы ключевых элементов и ее соединение с блоком принятия решений
Состояние каждого из ключевых элементов (КЭ) определяется текущим состоянием соответствующего ему участка дискретного плана внешней среды. Если КЭ соответствует целевому участку, он генерирует выходные сигналы (волны возбуждения) во всех направлениях, определяемых шаблоном соседства. Если КЭ соответствует свободному участку, то он проводит любой входной сигнал с заданной задержкой на связанные с ним КЭ. Если КЭ соответствует заблокированному участку (препятствию), он осуществляет блокирование входных сигналов по всем направлениям. Направление антиградиента фронта волны возбуждения в точке, соответствующей положению робота в среде, фиксируемое посредством блока принятия решений [9], определяет направление вектора оптимального перемещения робота к цели.
Как показано в работе [7], при использовании бионического метода адаптивного управления для планирования траекторий движения ММРП, функционирующих в среде с узкими проездами, необходимо дополнительно воспроизводить в матрице ключевых элементов тормозные квазиполя препятствий с целью оптимизации траектории по критерию безопасности. Элементы этих полей представляют собой величины задержек волны возбуждения свободных от препятствий КЭ. Использование тормозных регрессивных квазиполей позволяет «отодвинуть» фронт волны возбуждения, распространяющейся в матрице КЭ, от препятствий (см. рис. 2 [4]).
Применение данного подхода, совместно с расширением размеров препятствий, присутствующих на плане среды, на величину, равную половине ширины корпуса робота [9], позволяет существенно снизить вероятность столкновений с препятствиями, вызванных погрешностями исполнительных механизмов робота. Так как необходимость расширения размеров препятствий более чем на половину ширины корпуса робота при этом отсутствует, минимизируется также вероятность перекрытия существующих безопасных проходов к целевому объекту.
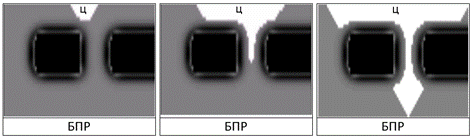
Рис. 2. – Визуализация процесса распространение волны возбуждения (показана белым светом) в матрице КЭ с учетом тормозных квазиполей препятствий (значения коэффициентов задержки КЭ показаны оттенками серого, препятствия – черным цветом).
Известные процедуры синтеза тормозных регрессивных квазиполей препятствий, базирующиеся на применении операции дистантного преобразования [10] или математической модели рецептивных полей клеток сетчатки [11], весьма сложны, а их реализация приводит к существенным временным и аппаратным затратам, что весьма критично для бортовых систем управления ММРП.
В данной работе предлагается подход к синтезу тормозных квазиполей препятствий, устраняющий недостатки известных подходов.
Суть предлагаемого подхода состоит в том, что значения коэффициентов задержки волны возбуждения ![]() , определяющие воздействие тормозных регрессивных квазиполей препятствий на свободные КЭ, не рассчитываются перед каждым актом принятия решений в соответствии с заданным алгоритмом, а загружаются в матрицу КЭ в виде априори вычисленных значений выбранной функции
, определяющие воздействие тормозных регрессивных квазиполей препятствий на свободные КЭ, не рассчитываются перед каждым актом принятия решений в соответствии с заданным алгоритмом, а загружаются в матрицу КЭ в виде априори вычисленных значений выбранной функции ![]() (ρ), где ρ - расстояние до кромки ближайшего препятствия. Порядок загрузки априори вычисленных значений функции
(ρ), где ρ - расстояние до кромки ближайшего препятствия. Порядок загрузки априори вычисленных значений функции ![]() (ρ) в матрицу КЭ определяется посредством волновой итерационной процедуры.
(ρ) в матрицу КЭ определяется посредством волновой итерационной процедуры.
Таким образом, для реализации предлагаемого подхода сначала необходимо определить функцию ![]() (ρ), задающую характер изменения тормозных квазиполей с изменением расстояния ρ до кромки ближайшего препятствия.
(ρ), задающую характер изменения тормозных квазиполей с изменением расстояния ρ до кромки ближайшего препятствия.
Известен ряд функций, используемых в различных методах автоматического планирования траектории движения к цели для оптимизации траектории по критерию безопасности за счет снижения приоритета выбора планировщиком участков дискретного плана, находящихся в заданной окрестности препятствий.
Примером такой функции может являться функция отталкивающего потенциала объектов-препятствий [4]:
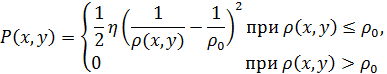 (1)
(1)
где ![]() – Евклидово расстояние между данным свободным участком плана и ближайшим участком, содержащим препятствие;
– Евклидово расстояние между данным свободным участком плана и ближайшим участком, содержащим препятствие; ![]() – максимальное расстояние, на котором отталкивающий потенциал препятствий продолжает оказывать влияние на синтезируемую траекторию;
– максимальное расстояние, на котором отталкивающий потенциал препятствий продолжает оказывать влияние на синтезируемую траекторию; ![]() – масштабирующий коэффициент.
– масштабирующий коэффициент.
В работе [5] планирование траектории движения осуществляется в базисе искусственной нейронной сети. Оптимизация траектории по критерию безопасности осуществляется за счет функции безопасности, которая определяет коэффициенты, снижающие значения синаптических весов входов нейронов, соответствующих участкам, находящимся в заданной окрестности препятствий:
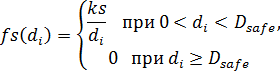 (2)
(2)
где ![]() – Евклидово расстояние между участком плана, соответствующим i-му нейрону и ближайшему участку, содержащему препятствие, ks – масштабирующий коэффициент;
– Евклидово расстояние между участком плана, соответствующим i-му нейрону и ближайшему участку, содержащему препятствие, ks – масштабирующий коэффициент; ![]() – безопасное расстояние, на котором функция безопасности
– безопасное расстояние, на котором функция безопасности ![]() не оказывает воздействие на синаптические веса входов нейронов.
не оказывает воздействие на синаптические веса входов нейронов.
В работе [11] для формирования регрессивных отталкивающих квазиполей препятствий используется алгоритм, в основе которого лежит применение функции Гаусса:
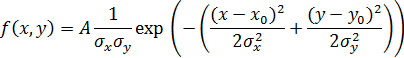 (3)
(3)
где x,y – координаты свободного участка на дискретном двухмерном плане: x0,y0 – координаты ближайшего объекта-препятствия; A – амплитуда функции Гаусса, σx и σy – стандартные отклонения для x, y.
Общим свойством приведенных функций является наличие нелинейного сегмента, убывающего с ростом расстояния до ближайшего препятствия и повышающего приоритет выбора участков, находящихся на отдалении от объектов-препятствий, в качестве сегментов синтезируемой траектории. Ввиду того, что во всех рассмотренных случаях скорость реакции функции на нелинейном сегменте задается эмпирически, наиболее гибким инструментом определения функции ![]() (ρ) на данном сегменте является использование полинома, выбор коэффициентов которого позволяет аппроксимировать любую из приведенных функций (1, 2, 3). Учитывая сказанное выше, функция
(ρ) на данном сегменте является использование полинома, выбор коэффициентов которого позволяет аппроксимировать любую из приведенных функций (1, 2, 3). Учитывая сказанное выше, функция ![]() (ρ) может быть задана в виде следующей системы уравнений:
(ρ) может быть задана в виде следующей системы уравнений:
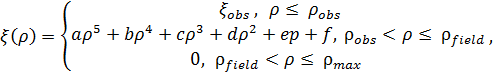 (4) (4) |
|
где ![]() – максимальное значение коэффициента задержки волны возбуждения, использующееся для расширения размеров препятствий (если свободный участок имеет значение коэффициента задержки
– максимальное значение коэффициента задержки волны возбуждения, использующееся для расширения размеров препятствий (если свободный участок имеет значение коэффициента задержки ![]() , равное
, равное ![]() , он помечается как препятствие);
, он помечается как препятствие); ![]() – максимальное расстояние, на котором тормозное регрессивное поле препятствия оказывает воздействие на коэффициенты задержки волны возбуждения свободных участков; a,b,c,d,e,f – коэффициенты полинома, задающего нелинейный сегмент функции
– максимальное расстояние, на котором тормозное регрессивное поле препятствия оказывает воздействие на коэффициенты задержки волны возбуждения свободных участков; a,b,c,d,e,f – коэффициенты полинома, задающего нелинейный сегмент функции ![]() , определяющий характер изменения тормозного квазиполя с изменением расстояния до ближайшего объекта-препятствия. Степень полинома была выбрана эмпирически. Значения коэффициентов аппроксимирующего полинома могут быть вычислены по координатам априори заданных точек. Примеры функций
, определяющий характер изменения тормозного квазиполя с изменением расстояния до ближайшего объекта-препятствия. Степень полинома была выбрана эмпирически. Значения коэффициентов аппроксимирующего полинома могут быть вычислены по координатам априори заданных точек. Примеры функций ![]() (ρ) при различных значениях коэффициентов аппроксимирующего полинома показаны на рисунке 3.
(ρ) при различных значениях коэффициентов аппроксимирующего полинома показаны на рисунке 3.
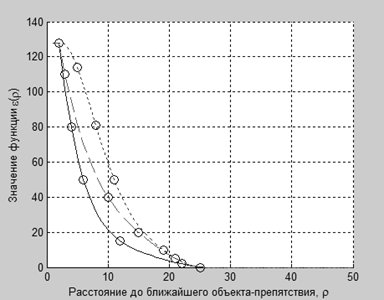
Рис. 3. – Примеры функций ![]() (ρ) при
(ρ) при ![]() ,
, ![]() ,
, ![]() и различных значениях коэффициентов аппроксимирующего полинома.
и различных значениях коэффициентов аппроксимирующего полинома.
Предлагаемый способ синтеза регрессивных квазиполей объектов-препятствий может быть сформулирован в виде следующего алгоритма:
- вычисляются значения решетчатой функции
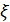 (ρi) (4), на всей области ее определения
(ρi) (4), на всей области ее определения 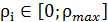 , где ρi - целые неотрицательные числа, определяющие нормированные значения расстояния до кромки ближайшего препятствия;
, где ρi - целые неотрицательные числа, определяющие нормированные значения расстояния до кромки ближайшего препятствия; - значения функции
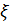 (ρi) упорядоченно сохраняются в массив коэффициентов задержи волны возбуждения таким образом, чтобы значение
(ρi) упорядоченно сохраняются в массив коэффициентов задержи волны возбуждения таким образом, чтобы значение 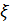 (ρi) было доступно по индексу i;
(ρi) было доступно по индексу i; - из текущего дискретного плана внешней среды, для которого производится синтез тормозных регрессивных квазиполей препятствий, исключаются целевые объекты. Участки дискретного плана среды, соответствующие объектам-препятствиям помечаются как целевые. После этого преобразованный дискретный план среды загружается в матрицу КЭ;
- в матрице КЭ воспроизводится очередная i-я итерация процесса распространения волны возбуждения;
- если КЭ находятся в возбужденном состоянии (его достигла волна возбуждения) и для него еще не было задано значение
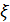 , коэффициент задержки волны возбуждения
, коэффициент задержки волны возбуждения 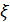 для данного КЭ задается равным значению элемента массива коэффициентов задержки волны возбуждения с индексом i;
для данного КЭ задается равным значению элемента массива коэффициентов задержки волны возбуждения с индексом i; - если все КЭ, соответствующие свободным участкам дискретного плана, находятся в возбужденном состоянии, процесс синтеза тормозных квазиполей препятствий останавливается, иначе переход к пункту 4.
Таким образом, волновая процедура выполняется в матрице КЭ дважды на каждой итерации алгоритма планирования траектории движения робота: первый раз для синтеза тормозных регрессивных квазиполей препятствий посредством предложенного алгоритма, а второй раз – для непосредственного синтеза траектории движения к целевому объекту на полученном дискретном плане среды с учетом загруженных в матрицу КЭ коэффициентов задержки ![]() .
.
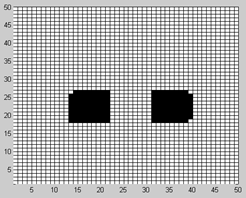
Пусть подсистемой формирования модели внешней среды получен дискретный план, графическое представление которого приведено на рисунке 4а. На рисунке 4б показан результат синтеза тормозных регрессивных квазиполей препятствий для данного дискретного плана, полученный посредством MATLAB Simulink модели приведенного выше алгоритма, при использовании функции ![]() (ρi), график которой изображен на рисунке 3 сплошной линией.
(ρi), график которой изображен на рисунке 3 сплошной линией.
Как видно из рисунка 4б, синтезируемые посредством предлагаемого алгоритма тормозные регрессивные квазиполя препятствий имеют форму концентрических квазиокружностей. Такая форма тормозных квазиполей препятствий связана с выбором входных задержек боковых и диагональных связей КЭ [7] (2 такта дискретного времени для боковых связей и 3 – для диагональных, см. рис. 1), при которых в матрице КЭ при воспроизведении волнового процесса аппроксимируется свойства двухмерного пространства с Евклидовой метрикой.
 |
|
|
а |
б |
Рис. 4. – Дискретный план среды с отмеченными черным цветом препятствиями (а) и результат синтеза тормозных квазиполей (б).
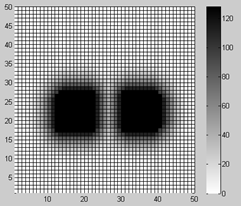
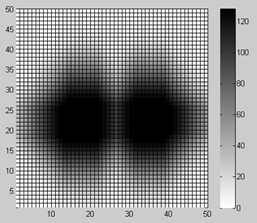
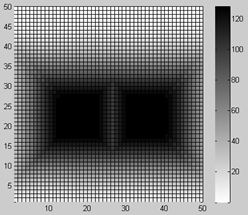
Легко убедиться, что при использовании входных задержек для прямых и диагональных связей равных единице, что соответствует метрике пространства Чебышева, синтезируемые тормозные квазиполя препятствий будут иметь прямоугольную форму (см. рис. 5а). При использовании задержек для прямых и диагональных связей равных 1 и 2 соответственно, что соответствует метрике пространства Минковского (метрика «Расстояние городских кварталов»), тормозные квазиполя будут иметь ромбовидную форму (см. рис. 5б).
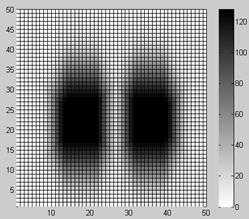
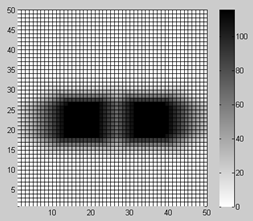
При использовании различающихся входных задержек ключевых элементов для «горизонтальных» (с «правым» и «левым» соседними КЭ в двухмерном представлении) и «вертикальных» (с «верхним» и «нижним» соседними КЭ) связей, может быть получена квазиэллиптическая форма синтезируемых квазиполей препятствий. Если входная задержка для горизонтальных связей больше входной задержки для вертикальных связей, синтезируемые тормозные квазиполя будут иметь «вытянутую» по вертикали форму (см. рис. 5в) и наоборот, если входная задержка для вертикальных связей больше входной задержки для горизонтальных связей, «вытянутую» по горизонтали форму (см. рис. 5г).
 |
|
|
а |
б |
|
|
|
|
в |
г |
Рис. 5. – Прямоугольная (а) и ромбовидная (б) формы синтезируемых тормозных квазиполей препятствий при воспроизведении в матрице КЭ метрики Чебышева и Минковского соответственно; «вытянутая» форма квазиполей при использовании различающихся входных задержек КЭ для «горизонтальных» и «вертикальных» связей (в, г)
Возможность синтеза тормозных регрессивных квазиполей препятствий квазиэллиптической формы может использоваться для минимизации эффекта оптических искажений (дисторсии, эффекта перспективы), вносимых системой технического зрения робота в модель внешней среды при использовании неметрических подходов к ее формированию.
Таким образом, предлагаемый способ синтеза тормозных регрессивных квазиполей препятствий предоставляет ряд инструментов их конфигурирования:
- изменение значения
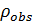 в системе уравнений (4) позволяет расширять размеры запрещенных для движения участков дискретного плана на заданную величину с целью учета собственных габаритов робота;
в системе уравнений (4) позволяет расширять размеры запрещенных для движения участков дискретного плана на заданную величину с целью учета собственных габаритов робота; - изменение значения
 и коэффициентов аппроксимирующего полинома в системе уравнений (4) позволяет задавать протяженность синтезируемых тормозных полей, а также характер изменения их влияния на коэффициенты задержки волны возбуждения свободных участков с изменением расстояния до ближайшего препятствия;
и коэффициентов аппроксимирующего полинома в системе уравнений (4) позволяет задавать протяженность синтезируемых тормозных полей, а также характер изменения их влияния на коэффициенты задержки волны возбуждения свободных участков с изменением расстояния до ближайшего препятствия; - изменение значений задержки на горизонтальных, вертикальных и диагональных входах ключевых элементов позволяет конфигурировать форму синтезируемых тормозных полей препятствий.
Для того чтобы предлагаемый алгоритм синтеза тормозных полей препятствий мог быть воспроизведен в матрице КЭ, реализованной аппаратно, в частности, в базисе программируемой логики, в схему КЭ [7] должны быть включены блоки конфигурируемой задержки волны возбуждения для вертикальных, горизонтальных и диагональных входов, а также блок памяти, реализующий логику сохранения коэффицинтов задержки волны возбуждения ![]() ключевыми элементами в ходе волновой процедуры (см. рис. 6). Кроме того, в схему бортового вычислительного модуля, решающего задачу автономного планирования траектории движения робота [7] должен быть включен блок памяти, хранящей значения функции
ключевыми элементами в ходе волновой процедуры (см. рис. 6). Кроме того, в схему бортового вычислительного модуля, решающего задачу автономного планирования траектории движения робота [7] должен быть включен блок памяти, хранящей значения функции ![]() (ρi) и шина коэффициентов задержки волны возбуждения
(ρi) и шина коэффициентов задержки волны возбуждения ![]() , обеспечивающая доступ каждого из КЭ к данному блоку памяти. На данную шину на каждой i-той итерации должен выставляться коэффициент
, обеспечивающая доступ каждого из КЭ к данному блоку памяти. На данную шину на каждой i-той итерации должен выставляться коэффициент ![]() , вычитанный из блока памяти по адресу i.
, вычитанный из блока памяти по адресу i.
Входы ключевого элемента, образующие связи с соседними ключевыми элементами на рисунке 6, обозначены как y1…y8 (их количество связано с выбором 8-ми точечного шаблона соседства). При этом входы y1 и y2 соответствуют «горизонтальным» связям, входы y3 и y5 соответствуют «вертикальным» связям, а входы y5…y8 - «диагональным» связям.
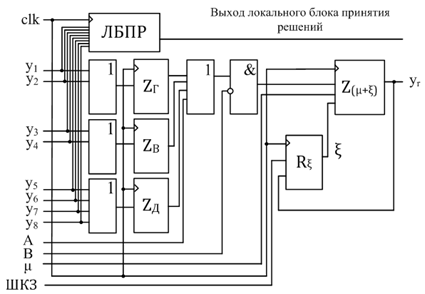
Рис. 6. – Структурная схема ключевого элемента
Входы A и B схемы ключевого элемента определяют соответствие данного КЭ целевому или заблокированному участку модели внешней среды соответственно. Блоки, реализующие входные задержки КЭ, обозначены как ZГ, ZВ и ZД соответственно. Блок задержки волны возбуждения, обозначенный на схеме КЭ как Z(μ+ξ), воспроизводит задержку волны возбуждения, определяемую суммарным значением коэффициентов μ (определяет трудность преодоления участка, зависящую от рельефа и типа подстилающей поверхности) и ![]() . Значение коэффициента
. Значение коэффициента ![]() синтезируется в ходе описанного выше волнового алгоритма и загружается в блок памяти Rξ посредством шины коэффициентов задержки (ШКЗ). Локальный блок принятия решений (ЛБПР) определяет направление, с которого волна возбуждения первой достигла входов КЭ.
синтезируется в ходе описанного выше волнового алгоритма и загружается в блок памяти Rξ посредством шины коэффициентов задержки (ШКЗ). Локальный блок принятия решений (ЛБПР) определяет направление, с которого волна возбуждения первой достигла входов КЭ.
Преимуществом предлагаемого способа синтеза тормозных регрессивных квазиполей препятствий в сравнении с бионическим алгоритмом [11], а также алгоритмами, в основе которых лежит операция вычисления Евклидова расстояния до кромки ближайшего препятствия (1,2), является отсутствие необходимости непосредственного вычисления коэффициентов задержки ![]() в процессе синтеза полей, так как значения функции
в процессе синтеза полей, так как значения функции ![]() (ρi) вычисляются и загружаются в буферную память априорно. Такой подход позволяет минимизировать ресурсы при аппаратной реализации функции синтеза тормозных регрессивных квазиполей препятствий.
(ρi) вычисляются и загружаются в буферную память априорно. Такой подход позволяет минимизировать ресурсы при аппаратной реализации функции синтеза тормозных регрессивных квазиполей препятствий.
Кроме того, при аппаратной реализации предложенного алгоритма (в частности, в базисе программируемой логики) за счет параллельной организации волновой итерационной процедуры синтеза тормозных регрессивных квазиполей препятствий, не подразумевающей непосредственного вычисления коэффициентов задержки ![]() , существенно сокращаются временные затраты на реализацию данной функции.
, существенно сокращаются временные затраты на реализацию данной функции.
Литература:
- Rohde M., Perlin V. PointCom: Semi-Autonomous UGV Control with Intuitive Interface. / SPIE Proceedings Vol. 6962, 2008;
- Пшихопов В.Х., Б.В.Гуренко Синтез и исследование авторулевого надводного мини-корабля «Нептун» [Электронный ресурс] // "Инженерный вестник Дона", 2013, №4. – Режим доступа: http://ivdon.ru/magazine/archive/n4y2013/1919 (доступ свободный) - Загл. с экрана. – Яз. рус.
- Кульченко А.Е. Алгоритмы функционирования автопилота робота-вертолета [Электронный ресурс] // "Инженерный вестник Дона", 2011, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2011/330 (доступ свободный) - Загл. с экрана. – Яз. рус.
- Khatib O. Real-Time obstacle avoidance for manipulators and mobile robotics/ In Proceedings of the IEEE International Conference on Robotics and Automation, 1985. – pp. 500 - 505.
- Weidong, Fan Changhong, Xi Yugeng. On-Line Safe Path Planning in Unknown Environments/ Chen– Taipei, Taiwan: Proc. of the 2003 IEEE International Conference on Robotics & Automation, 2003 . – pp. 4191 - 4196.
- Anthony Stentz. The Focussed D* Algorithm for Real-Time Replanning/. – In Proceedings of the International Joint Conference on Artificial Intelligence, 1995. – pp. 1652–1659;
- Бутов П.А., Доленко Ю.С. Реализация бортовой системы автономного планирования траектории движения для малогабаритных мобильных роботов в базисе SoC и FPGA технологий [Текст] // Сборник материалов Девятой Всероссийской научно-практической конференции «Перспективные системы и задачи управления», Таганрог, 2014, с. 502 – 513.
- Чернухин, Ю.В. Микропроцессорное и нейрокомпьютерное управление адаптивными мобильными роботами [Текст]: Учебно-научное издание / Ю.В. Чернухин. – Таганрог: ТРТИ, 1993. – 91 с.
- Чернухин Ю.В. Искусственный интеллект и нейрокомпьютеры [Текст]: Учебно-научное издание / Ю.В. Чернухин. - Таганрог: Изд-во ТРТУ, 1999, с. 105 – 133.
- Устройство управления автономным мобильным роботом [Текст] : пат. 139231 Рос. Федерация: МПК G 05 D 1/02 / Бутов П.А., Чернухин Ю.В.; заявитель и патентообладатель ЗАО «Научно-производственный комплекс «Бортовые интеллектуальные системы» - №2013153216/08; заявл. 27.11.13; опубл. 10.04.2014.
- Чернухин Ю.В., Бутов П.А., Доленко Ю.С. Нейросетевой подход к решению задачи локальной навигации интеллектуальными мобильными роботами в условиях, приближенных к реальной среде [Текст] // Известия ЮФУ. Технические науки, Таганрог, 2013. – № 5 (143). – с. 80-84;