Определение оптимальных значений переменных, характеризующих положение размеров сечений, при различных геометрических параметрах 3-D модели металлорежущего инструмента
Аннотация
В статье рассматривается методика определение оптимальных численных значений переменных, которые характеризуют положение определенных размеров на сечениях, при различных геометрических параметрах 3-D модели режущей части металлорежущего инструмента. Для расчета значений переменных используются интерполяционные полиномы Лагранжа.
Ключевые слова: металлорежущий инструмент, интерполяционные полиномы Лагранжа, размеры сечения.05.13.12 - Системы автоматизации проектирования (по отраслям)
На начальном этапе процесс проектирования металлорежущего инструмента (резца) начинается с расчета 3-D параметрического изображения. После создания 3-D модели инструмента разрабатывается чертеж с изображением ассоциативных видов, на основе указанной модели. Для вставки видов и сечений рассчитываются точки вставки ассоциативных изображений, которые определяются по средним значениям геометрических параметров определенного представителя МИ [1].
При разработке чертежей металлорежущего инструмента (резцов) с использованием параметрических 3-D моделей, как правило, используются однотипные изображения сечений, которые отличаются лишь своими размерами. Заметим, что в процессе разработки чертежей резцов на машиностроительных предприятиях как правило, используются два различных сечения, ориентация изображений которых зависит от положений секущих плоскостей. Первое сечение (А-А) определяется в главной секущей плоскости (Pt), которая, как известно перпендикулярна линии пересечения основной плоскости (Pv) и плоскости резания (Pn) в определенной точке [2]. Параметрическая 3-D модель резца с изображением на ней указанных координатных плоскостей представлена на рис. 1а. Второе сечение определяется во вспомогательной секущей плоскости, которая перпендикулярна вспомогательной режущей кромке. Таким образом, изображение первого сечения используется для задания формы передней поверхности резца, которая зависит от значения главного переднего угла (γ) и других геометрических параметров, и определения величины главного заднего угла (α) (см. рис. 1 б).
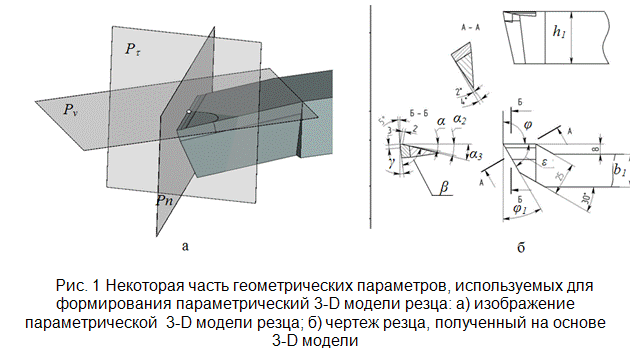
Изображение второго сечения определяет величину вспомогательного заднего угла (α1) и вспомогательного переднего угла (γ1) (см. рис. 1 б). При вставке изображений сечений, полученных на основе параметрических 3-D моделей металлорежущего инструмента (МИ) при различных значениях главного угла в плане (φ) и вспомогательного угла в плане (φ1) возможны ситуации, когда изображения некоторых размеров и размерных текстов пересекаются между собой.
На рис. 2а приведен пример фрагмента чертежа резца на станок МК6713. На данном чертеже ориентация сечения будет зависеть от главного угла в плане (φ) [3]. При значении угла φ =600 пересечение размерных линий и чисел не происходит, а при φ =300 соответственно происходит.
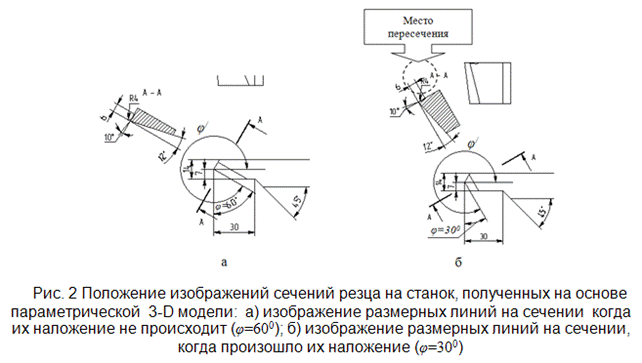
Для исключения ситуации пересечения размеров сечений определим оптимальные значения параметров j и c от угла поворота φ/ = 270+φ при различных значениях L2 (см. рис. 3). Геометрический смысл параметров j, c и L2 представлен на рисунке 3.
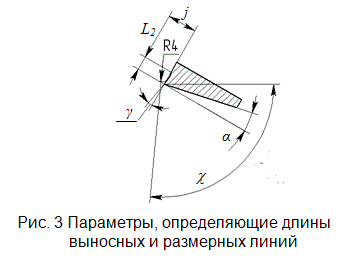
Заметим, что длина выносной линии, заданная значением параметра j должна принимать минимальное значение, чтобы общая площадь сечения была минимальна. Параметры j и c используются при создании линий построения и связанных узлов при нанесении размеров сечений.
В ходе графических построений были определены точки графиков j =f1 (φ/) и c =f2 (φ/) для разных значений L2 и φ/. Для расчета значений параметров j и c в зависимости от значений φ/ и L2 используем интерполяционные полиномы Лагранжа [4]. При этом в качестве исходных данных выступают совокупность точек Bi, 
и 
на отрезке [
, 
]. Положение точек Bi, …, 
определяются значением функционалов f1 (φ/), f2 (φ/). Положение данных точек определяется графическими построениями. Для интерполяции по n + 1 заданным точкам (jk, 
) k = 0, 1, …, n таким, что 
<
< …<
необходим полином степени n с n + 1 коэффициентами, который представляется в виде:
, (1)
где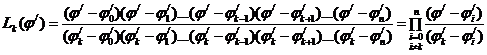 
.
Таким образом, задача интерполяции сводится к нахождению полиномов:
, 
. (2)
Для вычисления коэффициентов 
первого уравнения (2) требуется решить систему n+1 линейных уравнений с n-1 неизвестными:
. (3)
Точно таким же образом находятся коэффициенты второго уравнения (2) решением системы:
. (4)
На основе определенных узловых точек, представленных на рисунке 4а и 4б, для длин L2=2.5, L2=4, L2=6 получены следующие интерполяционные полиномы Лагранжа.
(5а)
(5б)
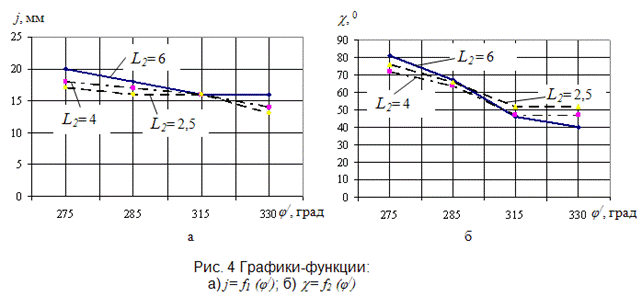
Таким образом, использование интерполяционных полиномов Лагранжа позволяет вычислить параметры, определяющие положение размерных линий и их ориентацию, которая будет зависеть от определенных геометрических параметров резца 3-D модели. Применение полиномов Лагранжа позволяет исключить ситуации, при которых происходит наложение изображений размеров друг на друга одного и того же сечения. Также вычисленные параметры размерных и выносных линий позволяют получить минимальную площадь, которую занимает сечение и принадлежащие ему размеры. В совокупности аналитические зависимости (5а, б) позволяют осуществлять автоматизированную корректировку положений размерных и выносных линий сечений при различной их ориентации на чертеже.
Литература
- 1.Шмуленкова, Е. Е. Определение оптимального положения базовых точек вставки ассоциативных видов параметрической 3-D модели для заданного множества представителей металлорежущего инструмента / Е. Е. Шмуленкова // Техника и технология. – М., 2011. – №4. – С. 39–43
2. Грановский, Г. И. Кинематика резания. / Г. И. Грановский. – М.: Масшгиз, 1948. – 200 с.
3.Фельдштейн, Е. Э. Металлорежущие инструменты: справочник конструктора / Е. Э. Фельдштейн, М. А. Корниевич. – Минск, 2009. – 1039 с.
4.Фокс, А. Вычислительная геометрия. Применение в проектировании и на производстве / А. Фокс, М. Пратт. – М. : Мир, 1982. – 304 с.