Графические оптимизационные модели многопараметрических технологических процессов легкой промышленности
Аннотация
В современных исследованиях в области многофакторных технологических процессов и решения задач их оптимизации часто, наряду с традиционными математическими методами планирования эксперимента, применяют методы математического (геометрического) моделирования. Такое моделирование проводится методами инженерной геометрии, практическая ценность которых заключается в графическом представлении функциональных зависимостей показателей качества от факторов и параметров, определяющих процесс с числом переменных более трех. Для обеспечения наглядности изображений и решения определенных технических задач в статье приведены алгоритмы определения оптимизационной области на основе чертежа Радищева. Построена графическая оптимизационная модель процесса соединения деталей швейных изделий.
Ключевые слова: Технологический процесс, оптимизация, моделирование, начертательная геометрия, многомерное пространство, чертёж Радищева, гиперплоскость, гиперповерхность, алгоритм, факторы, параметры
Инновации в легкой промышленности предопределяют необходимость решения сложных технических задач, требующих применения системного подхода к созданию моделей технологических процессов, в том числе и методов современной обработки информации [1].
В качестве примеров таких задач можно выделить следующие: поиск оптимальных условий проведения технологических процессов; оценка качества, прогнозирование свойств и характеристик объектов процесса в зависимости от параметров формирования и условий эксплуатации. Решение их традиционными классическими методами математического моделирования осложняется, прежде всего, из-за необходимости выявления закономерностей, связанных с учетом очень большого числа факторов и установления количественных взаимосвязей, определяющих в итоге заданное качество изготовляемых изделий.
В силу того, что математические модели многофакторных процессов характеризуются большим объемом вычислительных операций и отсутствием наглядного представления об объекте исследования, построение и анализ таких моделей, учитывающих множество независимых параметров и факторов, а так же выполнение предварительного анализа полученных данных и дальнейшего планирования эксперимента, удобно выполнять с использованием методов наглядного представления экспериментальных данных с помощью инженерной геометрии. Такой подход позволяет не только получить геометрически наглядную интерпретацию полученных результатов, он так же дает понимание конструктивной (геометрической) сущности алгоритмов оптимизации и решения поставленных задач при исследовании объекта: оценки степени выполнения заданных требований к создаваемым изделиям, выбора рациональных технологических режимов функционирования, выяснения закономерностей функционирования, анализа влияния факторов на показатели качества систем и т.д.
Обеспечение наглядности можно достичь с помощью многомерной начертательной геометрии, представляя исходные данные и полученные результаты в виде графической модели, которая представляет собой линейное или нелинейное подпространство многомерного пространства и отношений между ними. В научных работах по начертательной геометрии многомерного пространства предлагается несколько способов построения чертежей многомерных объектов на основе проекционного аппарата. Но с увеличением размерности пространства, большинство методов и подходов построения теряют свою наглядность, и все обоснования проводятся по аналогии с графической моделью трехмерного пространства. В связи с этим наиболее практичным для графического представления модели многомерного пространства является чертеж Радищева [2].
Методы многомерной геометрии на основе чертежа Радищева применяются к моделированию разнообразных многокомпонентных систем [3], а исследования таких моделей ведется с использованием методов исчислительной геометрии и теории параметризации [4]. Несмотря на то, что до сих пор остается нерешенным вопрос о достоверности решения задач с применением чертежа Радищева, ведется работа в направлении отыскания алгоритмов конструирования графически-оптимизационных моделей многофакторных процессов [5, 6].
Построение эксперимента и исследования свойств объектов или сложных моделей порой требуют значительных затрат и ресурсов. Таким образом, необходимо уделять серьезное внимание рациональной организации экспериментального изучения объектов. Графический анализ с использованием чертежа Радищева позволяет не только получить предварительное представление о моделируемом объекте или процессе, но и сделать предварительные выводы и скорректировать проходящий эксперимент.
Для обеспечения наглядности изображений и решения определенных геометрических задач на чертеже Радищева, для задания поверхностей используют каркасы. Такой подход применяется, когда графическая модель исследуемого процесса является гиперповерхность, как правило, для моделирования технологических процессов. Каркас, в данном случае, задается как однопараметрическое множество дискретного числа 1-поверхностей и позволяет задавать 2-поверхности однопараметрическим семейством 1-поверхностей.
Обоснование адекватности чертежа Радищева в качестве модели многомерного псевдоевклидова пространства с точки зрения аксиоматической теории, приведено в работе [7]. Доказанная адекватность чертежа Радищева позволяет достоверно использовать данную модель для решения задач оптимизации.
Гиперповерхность в 4-мерном пространстве может быть задана двухпараметрическим семейством 1-поверхностей, данный подход основывается на схеме расслоения многомерного пространства. Пусть гиперповерхность общего положения задана двухпараметрическим многообразием 1-поверхностей a (a1, a2, a3), b (b1, b2, b3), c (c1, c2, c3) (рис.1). Допустим, что задано две проекции 0-плоскости М (М1, М2). Необходимо построить третью проекцию при условии, что 0-плоскость М принадлежит гиперповерхности. Предположим, что гиперповерхность непрерывная гладкая и не имеет особенностей. Тогда в качестве 1поверхностей можем принять 1-поверхности второго порядка. Это допущение можно принять в малой области исследуемого процесса, который моделируется гиперповерхностью. Тогда выберем 2поверхность, которая проходит через 0-плоскость М1 и лежит в проецирующей гиперплоскости ∑13. Построим эту 2-поверхность на 2плоскости проекций x1x3и x1x2. Последняя будет представлена тройкой 1-поверхностей 111213, 212223, 313233.
Далее строим 1поверхность АВС, которая также проходит через М2 и лежит в проецирующей гиперплоскости ∆23. Получим её проекцию А3В3С3 на 2плоскости проекций x1x2. Так как по условию задачи 0-плоскость М принадлежит гиперповерхности, то её проекция М3 будет принадлежать А3В3С3.
При табуляции уравнения регрессии удобно принимать некоторые независимые переменные постоянными, дискретно изменяя их значения, а остальные будут определяться из расчетов. Тогда такие гиперповерхности на чертеже будут задаваться 1-поверхностями уровня или двойного уровня (рис. 2, 3).
Что бы изобразить поверхность отклика, заданную функцией
F(x1, x2, …, y1, y2, …) = 1,
где F – уравнение описывающее поверхность отклика, зависящее от n зависимых и независимых аргументов; x1, x2,… – независимые параметры процесса; y1, y2,…– факторы процесса,
необходимо последовательно фиксировать рассматриваемые параметры многофакторного процесса.
В таком случае, уравнение F будет преобразовано к виду
Ψ(y1, y2, …) = const.
Соответственно, находя корни уравнения Y, получается последовательность точек, проецируя которые на плоскости (x1, yi), получается соответствующий разрез исследуемой гиперповерхности, который отражает изменение фактора yi.
Рассмотрим алгоритм определения оптимизирующей области параметров в зависимости от значений независимых оптимизирующих факторов. Допустим, задана многокомпонентная система (x1, x2, …, xn) и несколько независимых между собой оптимизирующих факторов (f1, f2, …,fk), где fiпредставляет собой зависимость параметров и оптимизирующих факторов, для которых задан набор табличных данных, полученный в результате измерений, наблюдений или логическим путём.
Алгоритм определения оптимизирующей области параметров в зависимости от значений оптимизирующих факторов в общем виде будет выглядеть:
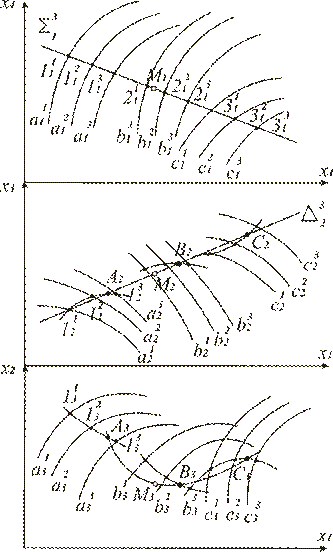
«Рис. 1. Гиперповерхность общего положения, заданная
двухпараметрическим многообразием 1-поверхностей»
1. Подбирается кривая определенного класса, имеющая определенное расположение относительно исходных точек для каждого фактора fi, и вычисляется уравнение Fi зависимости фактора fiот параметров (x1, x2,…, xn). Данная задача может быть решена, с помощью вычисления аппроксимирующих или интерполирующих кривых инцидентных всему или нескольким точкам из исходного набора данных.
2. Выбираются и задаются оптимальные значения факторов fi = fiоптим, которые будут геометрически являться 2-плоскостью уровня для факторов.
3. Исходя из оптимальных значений факторов, получаем функциональные зависимости выражающие зависимость параметров от оптимальных значений каждого из факторов:
F0(x1, x2,…, xn) = fiоптим
… (1)
Fк(x1, x2,…, xn) = fкоптим.
4. Далее оперируя полученными зависимостями (1) в пространстве n мы можем получить оптимизирующую область изменения параметров для заданных оптимальных значений факторов.
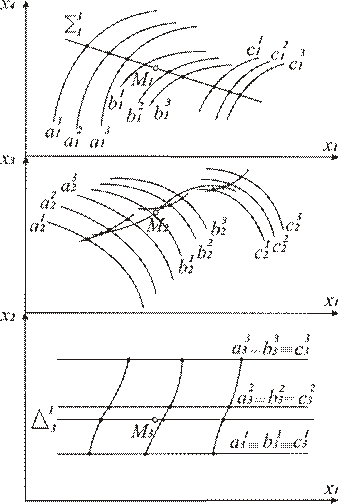
«Рис. 2. Задание гиперповерхности двупараметрическим многообразием 1-поверхностей уровня»
Этот алгоритм применим при различном числе параметров и оптимизирующих факторов, при этом нужно учитывать, что при n > 3 построить чертеж поверхности Fi(x1, x2, …, xn) = fiоптим на основе какого-либо проекционного аппарата крайне затруднено. При этом, если количество параметров совпадает с количеством факторов, то оптимизирующей областью будет одна или несколько 0-плоскостей. В том случае, если количество параметров больше количества оптимизирующих факторов, то размерность оптимизирующей области будет равна разности числа параметров и оптимизирующих факторов. Так же необходимо учитывать что, если число параметров меньше числа оптимизирующих факторов, т.е. n < k, то однозначно определить оптимизирующую область не удастся. В этом случае необходимо указывать область изменения оптимизирующих факторов.
Отметим, что рассматриваемые в настоящей работе вопросы методологического обеспечения решения технических задач являются общеприменимыми для различных технологических процессов легкой промышленности, вместе с тем основные иллюстративные материалы даны применительно к моделированию процесса соединения деталей швейных изделий.
Процессы соединения деталей швейных изделий, т.е. сборки и монтажа, занимают наибольший объём по трудоёмкости изготовления, и именно в этих процессах заложены максимальные резервы роста производительности труда и обеспечения качества швейных изделий. Показатели качества соединений деталей швейных изделий разнообразны. На показатели качества соединения, выполненного любым из существующих способов, оказывает влияние большое число различного рода факторов, наиболее значимыми из которых являются технологические параметры режимов обработки. Обеспечение заданного уровня качества соединений представляет собой сложную многофакторную задачу поиска оптимальных параметров, обеспечивающих соответствующий уровень качества.
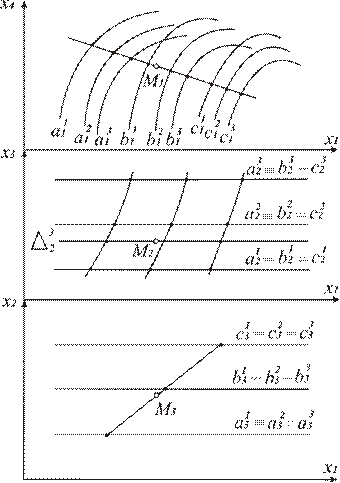
«Рис. 3. Задание гиперповерхности двупараметрическим
многообразием 1-поверхностей двойного уровня»
Ниточные способы соединения являются классическими и занимают наибольший удельный вес не только в швейной, но и в других отраслях легкой промышленности. Поэтому, разработанные алгоритмы определения оптимизирующей области значений параметров технологического процесса, в зависимости от значений оптимизирующих факторов, рассмотрены применительно к решению задач оптимизации параметров процесса ниточного соединения текстильных материалов.
Показатели качества ниточных соединений разнообразны и зависят от технических требований к изделию. Наиболее значимыми с практической точки зрения показателями качества ниточных соединений являются прочность шва, которая характеризуется разрывной нагрузкой в продольном или поперечном направлении, и жесткость. Выбранные показатели качества (оптимизирующие факторы) находятся в прямой зависимости от таких технологических параметров процесса, как длина стежка (количество стежков в 1 см), толщина швейной нитки и натяжение игольной нитки. При этом задача оптимизации сводится к выбору из широкого диапазона значений данных параметров определенных величин, обеспечивающих получение требуемого уровня оптимизирующих факторов. Таким образом, построение чертежей оптимизационных моделей целесообразно осуществлять по двум оптимизирующим факторам.
В качестве геометрической модели зависимости оптимизирующих факторов от параметров процесса ниточного соединения выбрана гиперповерхность, которая задана двупараметрическим семейством 1-поверхностей двойного уровня на чертеже Радищева (см. рис. 2).
Для построения чертежей гиперповерхностей оптимизирующих факторов проведены экспериментальные исследования разрывной нагрузки в поперечном направлении и жесткости ниточного шва от длины стежка при различных значениях толщины швейной нитки и натяжения игольной нитки. В качестве объектов исследования выбраны ниточные швы, выполненные на текстильных материалах челночными стежками.
Интервалы варьирования параметров процесса образования ниточного шва выбраны в зависимости от свойств текстильных материалов и возможностей швейной машины: параметр x1 –длина стежка – от 2 мм до 4 мм с шагом 1 мм; параметр x2 – натяжение игольной нитки – от 0,2 до 0,6 Н с шагом 0,2 Н; параметр x3 – толщина швейной нитки – 28, 32 и 37 текс.
Значение оптимального уровня разрывной нагрузки принято 200 Н. Анализ существующих экспериментальных исследований показал, что швейные изделия в процессе эксплуатации испытывают нагрузки не превышающие 160 Н. Таким образом, выбранный уровень Рр опт = 200 Н обеспечивает достаточный запас прочности. Значение оптимального уровня жесткости определялось жесткостью текстильного материала, на котором выполнялся шов, так чтобы жесткость шва не превышала жесткость текстильного материала более чем на 20%.
Построение чертежа оптимизационной модели трех параметров по двум оптимизирующим факторам выполнено в пространстве Е5, так как число параметров процесса равно трем и число оптимизационных факторов равно двум, в соответствии с разработанным алгоритмом (рис. 4). Координатные оси на чертеже обозначены следующими символами: входящие компоненты: x1 – длина стежка, мм;x2 – натяжение игольной нитки, Н; x3– толщина швейной нитки, текс; оси аргументов: x4= Рп – разрывная нагрузка ниточного шва в поперечном направлении, Н; x5 = Е – жесткость ниточного шва,мкН∙см2. Оптимизационной областью является 0-плоскость Р (Р1, Р2), координаты которой – х1Р= 3,15; х2Р= 0,45; х3Р= 33 – определяют значения параметров процесса образования ниточного шва, у которого Рп = Рп оптим = 200 Н, Е= Еоптим = 170000мкН∙см2.
Таким образом, графические оптимизационные модели позволяют, варьируя значения основных параметров процессов, выбирать режимы, обеспечивающие требуемые свойства шва, и могут быть использованы в качестве операционных карт выбора оптимальных режимов технологических процессов соединения деталей швейных изделий.
Для автоматизации процесса построения графических оптимизационных моделей создана компьютерная программа «Оптимизация процессов», позволяющая строить чертежи оптимизационных моделей и подбирать оптимальные значения основных параметров в зависимости от заданных значений нескольких оптимизирующих факторов. Компьютерная программа зарегистрирована в Отраслевом Фонде Алгоритмов и Программ.
![]()
![]()
![]()
![]()
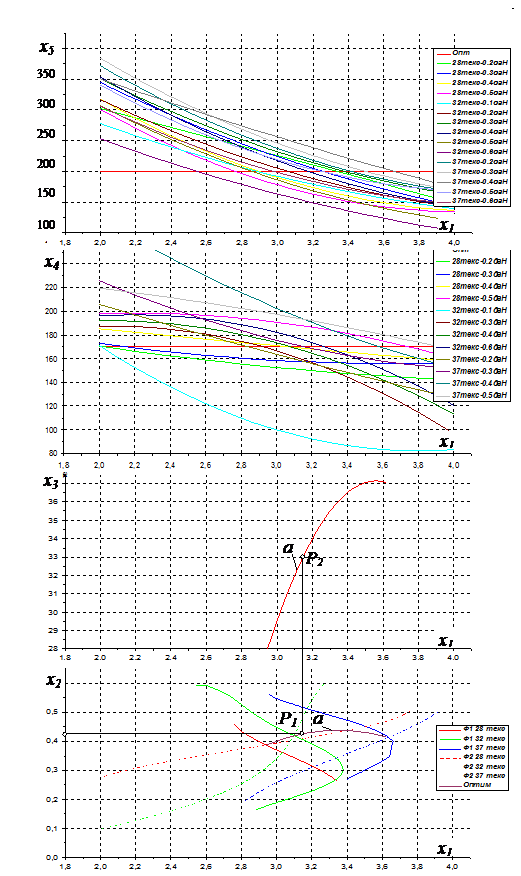
«Рис. 4. Графическая оптимизационная модель процесса ниточного соединениятекстильного материала (Джинс-стрейч) строчкой челночного стежка»
Литература:
1. Левков, К. Л. Инновационный процесс и инновационный инженер / К. Л. Левков, О. В. Фиговский // Инженерный вестник Дона. – 2012. – № 2. URL : http://www.ivdon.ru/magazine/archive/n2y2012/876 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Радищев, В. П. О применении геометрии четырех измерений к построению разновесных физико-химических диаграмм / В.П. Радищев // Изв. СФХА. – М., 1947. – Т. 15 – С. 129 – 134.
3. Волков, В. Я. Теория параметризации и моделирования геометрических объектов многомерных пространства и ее приложения: автореф. дис. д-ра техн. наук / В. Я. Волков. – М.: МАИ, 1983. – 27 с.
4. Волков, В. Я. Многомерная исчислительная геометрия : монография / В. Я. Волков, В. Ю. Юрков. – Омск: Изд-во ОмГПУ, 2008. – 244 с.
5. Волков, В. Я. Графические оптимизационные модели многофакторных процессов : монография / В. Я. Волков, М. А. Чижик. – Омск: Изд-во ОмГИС, 2009. – 101 с.
6. Чижик, М. А. Моделирование процессов соединения деталей швейных : монография / М. А. Чижик, В. Я. Волков. − Омск : ОГИС, 2010. − 147 с.
7. Устинова, О. В. Разработка оптимизационной модели процесса соединения текстильных материалов на основе чертежа Радищева многомерного пространства: Автореф. дис. к.т.н. – Омск: ОГИС, 2006 – 26 с.