Анализ RR интервального ряда водителя в условиях сильных помех с помощью wavelet-преобразования
Аннотация
Статья посвящена анализу состояния водителя транспортного средства методами, использующими данные RR-интервального ряда с помощью wavelet-преобразования. Рассмотрены результаты дискретного Wavelet-преобразования с помощью вейвлета Добеши 4-го порядка.
Ключевые слова: wavelet-преобразование, RR-интервальный ряд, интервалограмма
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Введение
Анализ RR интервального ряда водителя транспортного средства (ТС) позволяет оценить его психофизиологическое состояние и обеспечить надежную работу человеко-машинного комплекса «водитель – транспортное средство». Использование средств комфортного съема длительности RR интервалов предполагает применение таких средств, как сверхширокополосные (СШП) биорадары, чувствительные акселерометры и сейсмодатчики. Использование таких измерительных каналов на ТС неизбежно приводит к появлению ошибок при выявлении RR интервалов, как лишних RR, так и пропущенных. Собственно оценка RR-интервального ряда в основном основывается на работе Р.М. Баевского [1]. Практически все современные оценки состояния человека-оператора основаны на соотношении спектральных мощностей в низкочастотном (LF) и высокочастотном (HF) диапазонах.
Основной проблемой при разработке аппаратно-программных комплексов для оценки состояния водителя ТС является надежная регистрация этих параметров. Так, например, всего один импульсный артефакт движения способен создать широкополосный волнообразный спектральный «хвост». Если при предрейсовом контроле состояния водителя еще можно потребовать его неподвижности в течение нескольких минут, то для водителя это абсолютно неприемлемо. Множественные экстрасистолы на ритмограмме подобны случайным коротким импульсам, которые обогащают составляющую HF (в 2 – 5 раз), соответственно во столько же раз изменяется и отношение LF/HF. Таким образом, единичная экстрасистола или двигательный артефакт способны разрушить правильную оценку RR-интервального ряда на предмет наличия стрессовой ситуации или изменения состояния водителя. Классический подход при анализе RR-интервального ряда предполагает ручное удаление экстрасистол и артефактов с последующей интерполяцией RR-интервального ряда для сохранения целостности его временной структуры. Для автоматических комплексов анализа состояния водителя ТС эта методика не применима.
Целью данной работы является разработка методов обработки RR-интервального ряда, защищенных от артефактов движения и одиночных экстрасистол.
Материалы и методы.
Частотный анализ RR-интервального ряда можно производить без применения преобразования Фурье. Например, можно применить кратномасштабный анализ [2]. При его использовании артефакты движения и экстрасистолы в основном локализуются в области крупных масштабов, следовательно применив специализированную фильтрацию только в крупномасштабных детализациях сигналов, можно уменьшить влияние артефактов и экстрасистол на общую частотную структуру RR-интервального ряда.
Большие проблемы при анализе RR-интервального ряда возникают также из-за нестационарности ритма сердца. Решение проблемы - применение компактных во временной области носителей для более точной привязки ко времени наблюдаемых феноменов. Такой компактностью обладает Wavelet преобразование. Далее будет показано, что использование этого функционального преобразования, с одной стороны, позволяет анализировать нестационарные процессы, а с другой стороны, использовать оценки RR-интервального ряда, разработанные при спектральном Фурье анализе.
Для оценки применимости Wavelet преобразования для удаления артефактов из ритмограммы воспользуемся тестовыми записями RR интервалов из базы MIT-BIH [3]. Преимущество данных записей состоит в том, что каждый интервал снабжен маркером типа, т.е. можно включать в анализ и исключать из него по желанию любые виды артефактных интервалов.
В качестве инструментария использован пакет WaveletToolBox MatLab [3].
Загрузим RR интервальный ряд chf201 из базы MIT-BIH:
fid=fopen('v:\temp\RR wavelet\Данные RR\chf201.ecg');
a=fread(fid,[2,4000], '*uint8');
b=[1:4000];
bi=[1:10000];
k=0;
for i=1:4000
k=k+1;
b(k)=(1.0/128.0)*double(a(1,i)); % преобразование отсчетов в мсек
end;
m=0; % интерполяция сигнала и приведение к временной сетке 4.5 Гц.
for i=1:k-1
nl=floor(b(i+1)/0.22222);
aa=(b(i+1)-b(i))/nl;
for l=1:nl
m=m+1;
bi(m)=b(i)+(l-1)*aa;
end;
end;
b1=bi(1:m);
b1=detrend(b); % исключение линейного тренда из сигнала
b1=b1(1:1024);
figure(1);
plot(b);
title('Интервалограмма chf201 с артефактами (исходная)');
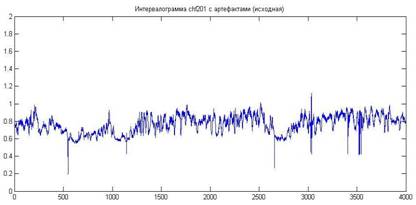
Рисунок 1 – Интервалограмма с артефактами.
На рисунке 1 изображена ритмограмма с многочисленными артефактами, один из которых находится в самом начале (первый интервал), а второй – на 542 интервале. Рассмотрим результат дискретного Wavelet- преобразования (три масштаба) с помощью вейвлета Добеши 4-го порядка:
w='db4';
[C,L]=wavedec(b1,8,w); % разложение исходного сигнала
[cd1,cd2,cd3,cd4,cd5]=detcoef(C,L,[1 2 3 4 5 6 7 8]);
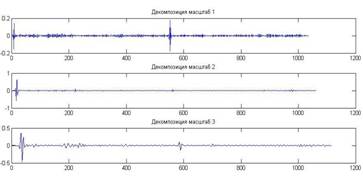
Рисунок 2 – Декомпозиции исходной интервалограммы.
Из рисунка 2 видно, что наиболее рельефно артефакты представлены на масштабах с меньшими номерами. Применим медианную фильтрацию к детализации 1 с помощью вызова функции cd1=medfilt1(cd1,5).
Результат показан на рисунке 3.
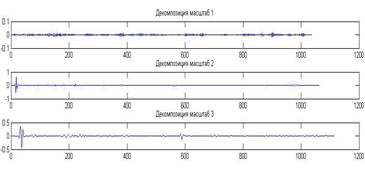
Рисунок 3 – Декомпозиции после медианной фильтрации.
На декомпозиции масштаба 1 артефакты исчезли, вместе с тем структура декомпозиции сохранилась.
Численные эксперименты показали, что для удаления артефатов движения и единичных экстрасистол достаточно применить нелинейную фильтрацию (например, медианную) к детализациям с крупными масштабами с последующим восстановлением сигнала при помощи обратного дискретного Wavelet- преобразования:
cd2=medfilt1(cd2,3); % медианная фильтрация детализации 2 с окном 3
cd3=medfilt1(cd3,5); % медианная фильтрация детализации 3 с окном 5
figure(2);
for i=559:1073
C(i)=cd1(i-558);
end;
for i=298:558
C(i)=cd2(i-297);
end;
for i=164:297
C(i)=cd3(i-163);
end;
sg=waverec(C,L,w); % восстановление сигнала
hold on
plot(b1);
p=plot(sg);
set(p,'Color','red');
title('Восстановленный сигнал');
hold off
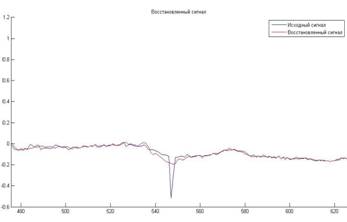
Рисунок 4 – Исходный и восстановленный сигналы в зоне артефакта при фильтрации декомпозиции 3.
Как видно из рисунка 4 высокочастотный артефакт заменен гладким сигналом, хорошо вписывающимся во временную структуру исходного сигнала.
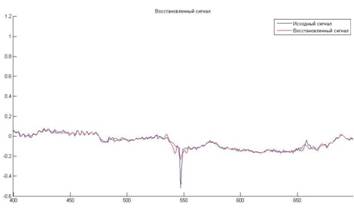
Рисунок 5 – Исходный и восстановленный сигналы в зоне артефакта при фильтрации декомпозиции 2.
Как видно из рисунка 5 высокочастотные составляющие сигнала восстановлены лучше, чем в случае, показанном на рисунке 4. Более правильных результатов можно достигнуть, если окно медианной фильтрации адаптируется к уровню декомпозиции.
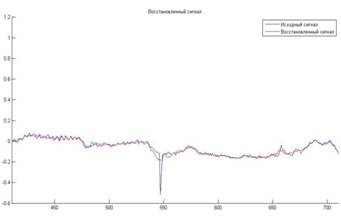
Рисунок 6 – Исходный и восстановленный сигналы в зоне артефакта при фильтрации декомпозиции 2 с шириной окна 3 и декомпозиции 3 с шириной окна 5.
Обсуждение результатов.
Из анализа рисунков видно, что наилучшие результаты при коррекции артефактов движения и единичных экстрасистол достигаются при одновременной нелинейной фильтрацией декомпозиций различного уровня, с шириной окна, адаптивной к уровню декомпозиции. Дальнейшее улучшение селективности алгоритма можно достигнуть, если медианную фильтрацию проводить выборочно, при превышении уровня некоторого адаптивного порога, различного для каждой декомпозиции.
Выводы
Для удаления артефактов движения и одиночных экстрасистол из ряда RR-интервалов можно использовать дискретное wavelet преобразование.
Применение дискретного wavelet преобразования позволяет проводить анализ нестационарного ряда RR-интервалов.
Наиболее хороший результат дает применение нелинейной медианной фильтрации, с окном, адаптивным к масштабу декомпозиции.
Результаты исследований, изложенные в данной статье получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта "Создание высокотехнологичного производства по изготовлению информационно-телекоммуникационных комплексов спутниковой навигации ГЛОНАСС/GPS/Galileo" по постановлению правительства №218 от 09.04.2010.
Список литературы:
1.Баевский Р.М. Математический анализ изменений сердечного ритма при стрессе / Р.М. Баевский, О.И. Кириллов, С.З. Клецкин, - М,: Наука, 1984, - 222 с
2.Чуи Ч. Введение в вэйвлеты: Пер. с англ./ Ч. Чуи. - М.: Мир, 2001.- 412с., ил.
3.Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB.-М.:ДМК / Н.К. Смоленцев // Пресс, 2008.- 448с.:ил.
4.The research resource for complex physiologic signals / URL: http://www.physionet.org