Алгоритм построения кубических интерполяционных сплайнов в задачах управления работой приводов с прогнозированием динамики нагрузки

Аннотация

Н. И. Гданский, А.В.Карпов, А.А. Бугаенко

  При использовании предсказания в управлении вращательным движением возникает необходимость построения дважды гладкой траектории, проходящей через ранее измеренные ее узловые точки. В качестве кусочно-полиномиальной кривой, обеспечивающей требуемую гладкость, рассмотрены интерполяционные кубические сплайны, которые на промежутках между узлами представляют собой кубические параболы, непрерывно соединяющиеся в узлах с гладкостью степени 2. При наложении дополнительных краевых условий, данные сплайны минимизируют ее суммарную кривизну.

Ключевые слова: Интерполяционные сплайны, задачи управления, алгоритмы прогнозирования, кинематические характеристики, сплайны Эрмита

05.13.06 - Автоматизация и управление технологическими процессами и производствами (по отраслям)

1. Введение

В цифровых системах управления вращательным движением при моделировании внешней нагрузки M = M (t, φ (t)), действующей на рабочий вал привода вращательного движения, в виде набора постоянных коэффициентов , имеющих смысл усредненных значений частных производных по времени t и углу поворота вала φ, мгновенную величину M (t, φ (t)) в общем случае можно представить в виде скалярного произведения , в котором вектор  называемый вектором кинематических характеристик, соответствующим модели , зависит только от t и производных j по t, имеющих порядок от первого до k – порядка модели .
При таком способе представления внешней нагрузки для расчета управляющего воздействия в данной системе используется работа A, которую должен совершать двигатель на заданном периоде импульсного управления T. Необходимая величина работы на отрезке изменения времени [t_i, t_i+1] как функция времени будет рассчитываться по формуле:
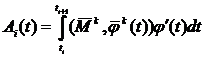.   (1)
Как следует из общего вида формул, получаемых после раскрытия интеграла (1), в них входят только производные φ по t, порядков от 1 до k. В частности, в случае использования модели нагрузки второго порядка максимальный порядок производных φ по t в формуле (1) равен 2. Поскольку сама зависимость φ  (t) в (1) яв но не входит, то это свойство решаемой задачи можно использовать для упрощения вспомогательной задачи интерполирования траектории перемещения вала по заданным ее узловым точкам.
Допустим, задан упорядоченный массив узлов Р_i = (t_i, φ_i) (i = 0, ..., n), лежащих на траектории перемещения. Для построения кусочно-полиномиальной кривой второй степени гладкости, проходящей через заданные узлы, наилучшим решением являются интерполяционные кубические сплайны [1, 2], которые на промежутках между узлами представляют собой кубические параболы, непрерывно соединяющиеся в точках t₁, ..., t_n-1 (называемых внутренними) с гладкостью степени 2. Также они обладают следующим важным свойством. Если наложить на сплайн в начальном и конечном узле краевые условия φ ”(t₀) = φ”(t_n) = 0, то он будет минимизировать функционал
,
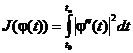который в случае перемещения равен минимуму работы, совершаемой инерционными нагрузками, создаваемыми перемещаемым звеном.
Рассмотрим глобальную переменную t. В математической форме полная совокупность геометрических условий относительно t, накладываемых на кубические параболы {S_i (t), i=1,2,…,n}, имеет вид:
а) φ(t) = S_i (t) при t_i-1 ≤ t ≤ ti; i =1, 2, …, n. – условие кусочности φ (t);
б) S_i (t_i-1) = P_i-1; S_i (t_i) = P_i, i = 1, 2, …, n – условия прохождения сплайна S_i (t) через заданные узлы ломаной P_i-1 и Pi;
в) , i = 1, …, n-1 – гладкость порядка 1 во внутренних узлах;
г), i=1, …, n-1 – гладкость порядка 2 во внутренних узлах;

д) S1”(t₀) = S_n”(tn) = 0 - краевые условия в начальном и конечном узлах.   (2)
Общепринятым методом построения кубических интерполяционных сплайнов является использование локальных сплайнов Эрмита. Данные сплайны строят по двукратным узлам t_i, в которых помимо значений S_i (t_i) заданы также величины первых производных S_i’(t_i). Поскольку в исходной задаче значения первых производных  S_i’(t_i) не задаются, их рассматривают в качестве неизвестных величин задачи, для решения которой составляют линейную систему уравнений. Матрица ее трёхдиагональна, что позволяет решать систему при помощи специальную упрощенной модификации метода Гаусса – метода прогонки [1, 2]. Основными стадиями метода прогонки являются:
1) расчет коэффициентов матрицы,
2) прямая прогонка,
3) обратная прогонка.
Расчет трудоемкости реализации алгоритма прогонки (таблица 1) показывает, что при максимальном сокращении расчетных формул вычислительные затраты при построении n сплайнов относительно невелики и составляют (после суммирования пп.1-3 таблицы 1): сложений 9n-3, умножений 8n-3, делений 4n-2.
Табл.1. Расчет минимального числа расчетных операций при построении n сплайнов

Существенной особенностью данного метода является то, что:
1) независимой переменной каждого сплайна S_i  является нормированная на отрезке [t_i-1; t_i ] локальная переменная τ_i = (t - t_i-1)/h_i, где h_i =( t_i - t_i-1),
2) результирующие сплайны S_i  имеют вид полиномов Эрмита,
При каждом расчете значений сплайна S_i  переход 1) от глобальной переменной t к локальной τ_i  при однократном расчете длин отрезков {} требует выполнения одного вычитания и одного деления.
Однако затраты при расчете полинома Эрмита 2) по сравнению с использованием схемы Горнера для кубического полинома (3 сложения и 3 умножения) слишком высоки и при большом числе расчетов значений сплайна S_i  необходимо перейти от полинома Эрмита к каноническом виду по локальной переменной τ_i. Данный переход при максимальном сокращении расчетных формул при построении n сплайнов требует относительно невысоких вычислительных затрат (п.4а таблицы 1): сложений 5n, умножений 5n.
Таким образом, для построения n сплайнов в форме канонических полиномов, зависящих от локальных переменных τ_i, необходимо затратить (сумма пп.1-4а таблицы 1): сложений 14n-3, умножений 13n-3, делений 4n-2.

Существенной особенностью интерполирования при решении рассмотренной выше задачи управления является то, что в формулы интегралов работ (1) входят только старшие коэффициенты {C₁,C₂,C₃} канонических кубических полиномов, зависящих от глобальной переменной t. Свободный коэффициент C₀ не входит. Переход от сплайнов в форме полиномов Эрмита, зависящих от локальных переменных τi, к каноническим полиномам по глобальной переменной t, требует значительных вычислительных затрат (п.4б таблицы 1). В сумме  для построения n сплайнов в форме канонических полиномов,

зависящих от глобальной переменной t, необходимо затратить (сумма пп.1-3 и 4б таблицы 1): сложений 28n-3, умножений 36n-3, делений 6n-2.

2. Постановка задачи

Для существенного снижения вычислительных затрат предложен прямой метод построения кубических интерполирующих сплайнов, в котором сплайны рассматриваются сразу в канонической форме по глобальной переменной t без использования полиномов Эрмита, а также не рассчитываются свободные коэффициенты сплайнов  C₀.  Такое интерполирование в отличие от традиционного назовем частичным.
Введем для упрощения расчетов новую относительную глобальную переменную   τ= t – t₀.
Постановка задачи. На плоскости τOφ задан набор из (n +1) точки вида , i = 0 ,…, n. Рассмотрим на отрезках [] кубические сплайны:
S_i (τ) = C₀ⁱ + C₁ⁱ t + C₂ⁱ t²/2 + C₃ⁱ τ³/3, i = 1, …, n.   (3)
Необходимо найти коэффициенты {C₁ⁱ, C₂ⁱ, C₃ⁱ} всех сплайнов {S_i (τ)} (i = 1, …, n) из условия гладкости степени 2 во внутренних узлах при заданных краевых условиях:
S₁”(0) = 0; S_n”(τ_n) = 0. (4)
Поскольку свободные коэффициенты C₀ⁱ сплайнов {S_i (τ)} не требуется определять, рассматриваем вместо S_i (τ) их первые производные, которые являются квадратными параболами вида:
D_i^τ) = (S_i ())τ’ = C₁ⁱ + C₂ⁱ t + C₃ⁱ τ².  (5)
Таким образом, частичное решение задачи интерполирования (без определения свободных коэффициентов) сплайнов S_i (τ), зависящих от глобальной переменной t, сведено к полному  расчету коэффициентов {C₁ⁱ, C₂ⁱ, C₃ⁱ, i = 1, …, n} соответствующих им квадратных парабол {Dⁱ(τ)} (5).

3. Прямой метод частичного решения задачи интерполирования

Для решения задачи полного расчета коэффициентов {C₁ⁱ, C₂ⁱ, C₃ⁱ, i = 1, …, n} квадратных парабол {D_i(τ)}, зависящих от глобальной переменной t, предложено использовать упрощённый (по сравнению с прогонкой, основанной на использовании полиномов Эрмита) метод, основная идея которого заключается в непосредственном расчете искомых коэффициентов без использования промежуточных представлений. Поэтому метод назван прямым.
Для определённости параболу D¹(τ) будем называть начальной, параболы D₂(τ) - D^n-1(τ) – внутренними, D^_n(τ) – конечной. Как и в методе прогонки, в предлагаемом методе для расчета искомых коэффициентов используем прямой и обратный ход.
Прямой ход.
Основная идея прямого хода заключается в том, что старший коэффициент текущей параболы D_i(τ) (i = 1, …, n-1) линейно выражается через старший квадратный коэффициент C₃ⁱ⁺¹ следующей за ней параболы Dⁱ⁺¹(τ, а свободный C₁ⁱ  и линейный C₂ⁱ коэффициенты параболы Dⁱ(τ) выражаются C₃ⁱ:
C₃ⁱ = A₃ⁱ C₃ⁱ⁺¹ + B₃ⁱ;
C₁ⁱ = A₁ⁱ C₃ⁱ + B₁ⁱ;
C₂ⁱ = A₂ⁱ C₃ⁱ + B₂ⁱ.    (6)
Отдельно рассмотрим начальную параболу D¹(τ), внутренние параболы D²(τ) - D^n-1(τ) и конечную Dⁿ(τ).
1. D¹(τ). Из условия S₁”(0) = 0 следует: (D₁(0))’ = C21+C31×0 = 0. Отсюда получаем: C₂¹ = 0. При этом для коэффициента C₂¹: A₂¹ = В₂¹ = 0.   (7)

Из условий прохождения сплайна S¹(τ) через точки  и  следует:
S₁ τ₀= 0) = C₀¹ = φ₀;    S₁ (τ₁) = C₀¹+ C₁¹ τ₁ + C₂¹ τ₁²/2 + C₃¹ τ₁³/3 = φ₁ .
Вычтем из второго соотношения первое с учетом C₂¹ = 0:
C₁¹τ₁ + C₃¹ τ₁³/3 = Δφ₁, где Δ_φ1 = φ₁ - φ₀.
Из этого равенства выразим линейную зависимость C₁¹ (C₃¹):
C₁¹ = Δφ₁ /τ₁ - C₃¹ τ₁²/3 = A₁¹ С₃¹ + В₁¹; A₁¹ = -τ₁² /3; В₁¹ = Δφ₁ /τ₁.    (8)
Расчетные формулы для выражения младших коэффициентов C₁¹ и C₂¹ начальной параболы через старший C₃¹ следующие:
A₁¹ = -τ₁²/3; В₁¹ = Δφ₁ /τ₁;       
A₂¹ = 0; В₂¹ = 0.     (9)      
Выражение (6) для старшего коэффициента C₃¹ у начальной параболы определяется при анализе параболы D²(τ).
2. Рассмотрим внутренние параболы Dⁱ(τ), i = 2, …, n -1.
К началу их анализа для предыдущей параболы D^i-1(τ) известны линейные зависимости:
C₁^i-1 = A₁^i-1 C₃^i-1 + В₁^i-1;
C₂^i-1 = A₂^i-1 C₃^i-1 + В₂^i-1.  (10)
Подставим формулы парабол D^i-1 (τ) и Dⁱ (τ)  в условия гладкости второй степени в узле τ = τ_i-1 для сплайнов S_i-1 (τ) и S_i (τ)  (S_i-1’ (τ_i-1) = S_i’ (τ_i-1); S_i-1”(τ_i-1) = Si”(τ_i-1)):
C₁^i-1 + C₂^i-1 τ_i-1 + C₃^i-1 τ_i-1² = C₁ⁱ + C₂ⁱ τ_i-1 + C₃ⁱτ_i-1²;
C₂^i-1 + 2C₃^i-1 τ_i-1 = C₂ⁱ + 2C₃ⁱ τ^i-1.
Умножая обе части второго соотношения на (-τ_i-1), складываем его с первым. При этом получим систему уравнений более простого вида:
C₁^i-1 - C₃^i-1 τ_i-1² = C₁ⁱ - C₃ⁱ τ_i-1²;
C₂^i-1 + 2C₃^i-1 τ_i-1 = C₂ⁱ + 2C₃ⁱ τ_i-1.
Подставим в уравнения полученной системы зависимости (10):
(A₁^i-1 - τ_i-1²)C₃^i-1 + В₁^i-1 = C₁ⁱ - C₃ⁱ τ_i-1²;
(A₂^i-1 +2_τi-1) C₃^i-1 + В₂^i-1 = C₂ⁱ + 2C₃ⁱ τ_i-1. (11)
Из условий S_i (τ_i-1) = φ_i-1; S_i (τ_i) = φ_i получим уравнение:
C₁ⁱ + C₂ⁱ(τ_i-1 + τ_i) /2 + C₃ⁱ(τ_i-1² + τ_i-1τ_i + τ_i²) /3 = Δφ_i / Δτ_i,  (12)
где Δφ_i = Δφ_i - φ_i-1, Δτ_i = τ_i - τ_i-1.
Складывая (12) с первым уравнением (11) и вторым, умноженным на (τ_i-1 + τ_i) /2, получим соотношение, содержащее только коэффициенты C₃^i-1 и C₃ⁱ:
(A₁^i-1 - τ_i-1²)C₃^i-1 + В₁^i-1 + (A₂^i-1 + 2τ_i-1) C₃^i-1(τ_i-1 + τ_i) /2 + В₂^i-1(τ_i-1 + τ_i) / 2 + C₃ⁱ(τ_i-1² + τ_i-1τ_i + τ_i²) /3 = Δφ_i / Δτ_i - C₃ⁱ τ_i-1² + 2C₃ⁱτ_i-1 (τ_i-1 + τ_i) / 2.
Преобразуя его, выразим C₃^i-1 через C₃ⁱ:
C₃^i-1 [A₁^i-1 + A₂^i-1(τ_i-1 + τ_i) /2 + τ_i-1ti] = C₃ⁱ[-(τ_i-1² + τ_i-1τ_i + τ_i²) /3 + τ_i-1τ_i] + Δφ_i / Δτ_i-1 - В₁^i-1 - В₂^i-1(τ_i-1 + τ_i)/2;
C₃^i-1 = A₃^i-1 C₃ⁱ + B₃^i-1;
где τ_(i)кв =t_i²; A₃^i-1 = - Δτ_(i)кв / (3К); B₃^i-1 = (Δφ_i / Δτ_i - В₁^i-1 - В₂^i-1 τ_icp) /К;
τ_icp = (τ_i-1 + τ_i) /2  ;  К = A₁^i-1 + A₂^i-1τ_icp + τ_i-1t_i. (13)
После подстановки (13) в уравнения системы (11) выражаем из них искомые зависимости C₁ⁱ(C₃ⁱ) и C₂ⁱ(C₃ⁱ):
C₁ⁱ = (A₁^i-1 - τ_i-1²)C₃^i-1 + В₁^i-1 +C₃ⁱ τ_i-1² = (A₁^i-1 - τ_i-1²)(A₃^i-1 C₃^i-1 + B₃^i-1) + В₁^i-1 +C₃ⁱ τ_i-1² = A₁ⁱ C₃ⁱ + B₁ⁱ,
где  F_i = A₁^i-1 - τ_(i-1)кв; A₁ⁱ = A₃^i-1 F_ⁱ + τ_(i-1)кв; B₁ⁱ = B₃^i-1 F_i + В₁^i-1;
C₂ⁱ = (A₂^i-1 +2τ_i-1) C₃^i-1+ В₂^i-1 - 2C₃ⁱ τ_i-1 = (A₂^i-1 +2τ_i-1) (A₃^i-1 C₃^i-1 + B₃^i-1)+ В₂^i-1 - 2C₃ⁱ τ_i-1 =A₂ⁱ C₃ⁱ + B₂ⁱ;
где τ_(i-1)у2 =2τ_i-1; Gⁱ = A₂^i-1 + τ_^(i-1)у2; A₂ⁱ = A₃^i-1 Gⁱ - τ_(i-1)у2; B₂ⁱ = B₃^i-1 Gⁱ + В₂^i-1.  (14)

Расчетные формулы для выражения младших коэффициентов C₁ⁱ и C₂ⁱ  и старшего коэффициента C₃^i-1 параболы D^i-1 через старший коэффициент C₃ⁱ параболы Dⁱ следующие:
τ_(i-1)кв=τ_(i-1) ²; τ_(i)кв =τi²; τ_icp = (τ_i-1 + τ_i) /2 ;  Δφ_i = Δφ_i - φ_i-1, Δτ_i = τ_i - τ_i-1;
К = A₁^i-1 + A₂^i-1τ_icp + τ_i-1τ_i; Fⁱ = A₁^i-1 - τ_(i-1)кв; τ_(i-1)у2 =2τ_i-1; Gⁱ = A₂^i-1 + τ_(i-1)у2;
A₃^i-1 = - Δτ_(i)кв / (3К); B₃^i-1 = (Δφ_i / Δτ_i - В₁^i-1 - В₂^i-1 τ_icp) /К;
A₁ⁱ = A₃^i-1 Fⁱ + τ_(i-1)кв; B₁ⁱ = B₃^i-1 Fⁱ + В₁^i-1;
A₂ⁱ = A₃^i-1 Gⁱ - τ_(i-1)у2; B₂ⁱ = B₃^i-1 Gⁱ + В₂^i-1.  (15)
3. Конечная парабола Dⁿ(τ).
К началу ее анализа для предыдущей параболы D^n-1(τ) известны зависимости:
C₁^n-1 = A₁^n-1C₃^n-1 + В₁^n-1;
C₂^n-1 = A₂^n-1 C₃^n-1 + В₂^n-1.    (16)
Из условий гладкости второй степени в предпоследнем узле τ = τ _n-1  для сплайнов S_n-1(t) и S_n(τ) (S _n-1’(τ_{n -1}) = S_n’(τ_{n -1}); S _n-1”(τ_{n -1}) = Sn”(τ_{n -1})) получим:
C₁^n-1 + C₂^n-1τ^n-1 + C₃^n-1 τ _{n -1}² = C₁ⁿ + C₂ⁿ τ _{n -1} + C₃ⁿ τ _{n -1}²;
C₂^n-1 + 2C₃ ^n-1 τ^n-1 = C₂ⁿ + 2C₃ⁿ τ_{n -1}.
Аналогично умножаем обе части второго соотношения на (-τ_n-1), складываем его с первым и получаем систему более простого вида:
C₁^n-1 - C₃^n-1 τ_{n -1}² = C₁ⁿ - C₃ⁿ τ_{n -1}²;
C₂^n-1 + 2C₃^n-1τ _{n -1} = C₂ⁿ + 2C₃ⁿ τ _{n -1}.
Подставим в уравнения системы зависимости (16):
(A₁^n-1 - τ_{n -1}²)C₃^n-1 + В₁^n-1 = C₁ⁿ - C₃ⁿ τ^_n-12;
(A₂^n-1 + 2τ_{n -1})C₃^n-1 + В₂^n-1 = C₂ⁿ + 2C₃ⁿ τ _{n -1}.  (17)
Аналогично из условий S_n(τ_n-1) = φ _{n -1}; S_n(τ_n ) = φ_n получим уравнение:
C₁ⁿ + C₂ⁿ(τ^{_{n -1}} + τ_n )/ 2 + C₃ⁿ(τ_{n -1}² + τ _{n -1} τ _n  + τ _n ²)/ 3 = Δ φ_n / Δτ _n,   (18)
где Δ φ _n = Δ φ_n  - φ _{n -1}, Δτ _n = τ _n - τ _{n -1}.
Дополнительно для данной параболы из второго краевого условия (4) получим еще одно уравнение:
C₂ⁿ + 2C₃ⁿ τ_n = 0.  (19)
Четыре уравнения системы (17) – (19) содержат 4 неизвестных коэффициента: C₃^n-1; C₁ⁿ ; C₂ⁿ; C₃ⁿ. Найдем их величины.
Выразим из (17) C₂ⁿ (C₃ⁿ):
C₂ⁿ = A₃ⁿ C₃ⁿ + B₃ⁿ,
где A₃ⁿ = - 2τ_n; B₃ⁿ = 0.     (20)
Полученное выражение подставим во второе выражение (17) и найдем зависимость C₃^{n -1} (C₃ⁿ):
(A₂ ^{n -1} + 2τ_{n -1})C₃ ^{n -1} + В₂ ^{n -1} = - 2C₃ ⁿ τ_n + 2C₃ ⁿ τ_{n -1};
C₃ ^{n -1} = A₃ ^{n -1} C₃ ⁿ + B₃ ^{n -1},
где A₃^{n -1} = - 2Δ τ_n / (A₂ ^n-1 + 2τ_{n -1}); B₃ ^{n -1} = - В₂ ^{n -1} / (A₂ ^n-1 + 2τ_{n -1}).   (21)
Подставляя данную зависимость в первое уравнение (17), найдем из него выражение для C₁ⁿ (C₃ⁿ):
(A₁ ^{n -1} - τ _{n -1}²)[-(2Δ τ _n C₃ ⁿ + В₂ ^{n -1})/(A₂ ^{n -1} + 2τ_{n -1})] + В₁ ^{n -1} = C₁ⁿ - C₃ ⁿ τ _{n -1}²;
C₁ ⁿ = A₁ ⁿ C₃ ⁿ + B₁ ^n,
где A₁ ⁿ = [-2Δ τ_n (A₁ ^{n -1} - τ_n-1²)/(A₂ ^{n -1} + 2τ _{n -1}) + τ _{n -1}²];
B₁ ⁿ =В₂ ^{n -1} (A₁ ^{n -1} - τ_{n -1}²)/(A₂ ^{n -1} + 2τ_{n -1})+В₁ ^{n -1.}   (22)
Подставляя зависимости (20) и (22) в уравнение (18), найдем из него выражение для коэффициента C₃ⁿ:
[-2Δ τ_n (A₁^{n -1} - τ _{n -1}²) / (A₂ ^{n -1} + 2τ _{n -1}) + τ_{n -1}²]C₃ ⁿ + В ₂ ^{n -1}(A₁ ^{n -1} - τ_{n -1}²)/(A₂ ^{n -1} + 2τ_{n -1}) + В1 ^{n -}1 - 2C₃ ⁿ τ_n(τ_{n -1} + τ_n)/ 2 + C₃ ⁿ(τ_{n -1}² + τ_{n -1} τ_n + τ_n ²)/ 3 = Δ φ_n / Δ τ_n;

C₃ ⁿ =[Δ φ_n/Δ τ_n-В₂ ^{n -1}(A₁ ^{n -1} - τ_{n -1}²)/(A₂ ^{n -1} + 2τ^n-1)-В₁^{n -1}]/[-2Δτ _n(A₁^{n -1}-τ _{n -1}²) / (A₂ ^{n -1}+2τ_{n -1})-2Δτ_n (2τ_n1+τ_n)/3].   (23)                                                                                                                     
Таким образом, для конечной параболы Dⁿ((τ) величина старшего коэффициента C₃ⁿ определяется не зависимостью вида (6), а формулой (23).
Для сокращения числа расчетных операций предложен следующий алгоритм расчета коэффициентов конечной параболы {C₁ⁿ; C₂ⁿ; C₃ ⁿ}и значения старшего коэффициента C₃ ^{n -1} параболы D^{n -1}(τ):
C₃ ⁿ =[Δ φ_n/Δ τ_n-В₂ ^{n -1} Е ⁿ -В₁^{n -1}]/[F ⁿ( Е ⁿ+(G ⁿ+Δ τ_n)/3];
где t_(n-1)кв=t_{n -1}²;G ⁿ=2Δ τ_{n -1}; H ⁿ=1/(A₂ ^n-1+G ⁿ); Е ⁿ=(A₁^{n -1}-Δ τ _(n-1)кв)H ⁿ; F ⁿ =-2Δ τ _n;
C₁ⁿ = [F ⁿЕ ⁿ + τ_{n (n -1)кв}] C₃ ⁿ + В₂ ^{n -1}Е ⁿ +В₁ ^{n -1};
C₂ⁿ = (- 2τ_n) A₃ⁿ C₃ⁿ;
C₃ ^{n -1} = F ⁿ H ⁿ C₃ ⁿ - В₂ ^{n -1}H ⁿ.   (24)
Обратный ход.
Заключается в последовательном расчете коэффициентов оставшихся квадратных парабол Dⁱ(τ) i = n-1,…,1. Выполняется в последовательности, обратной прямому ходу.
Для каждой параболы Dⁱ(τ) (i=n-1,…,1), по уже рассчитанному значению старшего коэффициента C₃ⁱ⁺¹ параболы Dⁱ⁺¹(_t) по формулам (6) вначале рассчитывается старший коэффициент  C₃ⁱ , а по нему – младшие C₁ⁱ и C₂ⁱ.

4. Расчетный алгоритм и оценка его трудоемкости
Начальные данные: координаты точек , (i = 0, …, n), τ₀ = 0.
Необходимо определить: массивы коэффициенты {C₁ⁱ, C₂ⁱ, C₃ⁱ} набора сплайнов {S_i (τ} (i = 1, …, n), обеспечивающих гладкость второй степени во внутренних узлах при краевых условиях: S₀’(0) = 0; S_{n -1}”(τ_n) = 0.
Начальные действия. Вводим вспомогательные массивы{A₃ⁱ}, {В₃ⁱ}, {A₁ⁱ}, {В₁ⁱ}, {A₂ⁱ}, {В₂ⁱ}, в которых номера элементов изменяются от 1 до n -1. Поскольку в расчетах коэффициентов соседних парабол повторяются вычисления квадратов значений времени τ_i, то перед началом вычислений предварительно рассчитываем их:
τ_(i)кв =τ_i²; 1, …, n . (25)
Шаг 1. Прямой ход. Расчет вспомогательных коэффициентов A₁¹, В₁¹, A₂¹, В₂¹ для начальной параболы D¹(τ). Из (9) следует:
A₁¹ = -τ_(1)кв / 3;   В₁¹ = (φ₁ - φ₀)/τ₁;   A₂¹ = В₂¹ = 0.   (26)
Шаг 2. Прямой ход. Цикл по внутренним параболам (i = 1, …, n -1). Расчет вспомогательных коэффициентов A₁ⁱ, В₁ⁱ, A₂ⁱ, В₂ⁱ для внутренней параболы Dⁱ(τ), а также коэффициентов A₃^i-1, В₃^i-1 для параболы D^i-1(τ) выполняем по формулам (15):
τ_icp = (τ_i-1 + τ_i) /2 ;  Δφ_i = Δφ_i - φ_i-1, Δτ_i = τ_i - τ_i-1;  К = A₁^i-1 + A₂^i-1τ_icp + τ_i-1τ_i;
Fⁱ = A₁^i-1 - τ_(i-1)кв; τ_(i-1)у2 =2τ_i-1; Gⁱ = A₂^i-1 + τ_(i-1)у2;
A₃^i-1 = - Δτ_(i)кв / (3К); B₃^i-1 = (Δφ_i / Δτ_i - В₁^i-1 - В₂^i-1 τ_icp) /К;
A₁ⁱ = A₃^i-1 F_i + τ_(i-1)кв; B₁ⁱ = B₃^i-1 Fⁱ + В₁^i-1;
A₂ⁱ = A₃^i-1 Gⁱ - τ_(i-1)у2; B₂ⁱ = B₃^i-1 G_i + В₂^i-1.  (27)
Шаг 3. Прямой ход. Расчет коэффициентов C₃n, C₁n, C₂n, C₃ ^n-1 выполняем по формулам (24):
G ⁿ=2τ_{n -1}; H ⁿ=1/(A₂ ^n-1+G ⁿ); Е ⁿ=(A₁^{n -1}-τ _(n-1)кв)H ⁿ; F ⁿ =-2Δτ _n;
C³ _n =[Δ_φn/Δ_tn-В₂ ^{n -1} Е _n -В₁^{n -1}]/[F ⁿ( Е ⁿ+(G ⁿ+τ_n)/3];
C_¹n = [F ⁿЕ ⁿ + τ _{(n -1)кв}] C₃ ⁿ + В₂ ^{n -1}Е n +В₁ n -1;
C₂ⁿ = (- 2τ_n) A₃ⁿ C₃ⁿ;
C₃ ^{n -1} = F ⁿ H ⁿ C₃ ⁿ - В₂ ^{n -1}H ⁿ (28)
Шаг 4. Обратный ход. Цикл по параболам с номерами i = n -1, …, 1. Расчет их коэффициентов C₁ⁱ, C₂ⁱ, C₃ⁱ.
C₃ⁱ = A₃ⁱ C₃ⁱ⁺¹ + B₃ⁱ;

C₁ⁱ = A₁ⁱ C₃ⁱ + B₁ⁱ;
C₂ⁱ = A₂ⁱ C₃ⁱ + B₂^i.      (29)                                                                                                     
Замечание. Если необходимо найти свободные коэффициенты сплайнов C₀ⁱ, например – для визуализации формы получаемых сплайнов с целью проверки качества получаемых решений, то их проще всего найти по формуле:
C₀ⁱ = φ_i - C₁ⁱ τi - C₂ⁱ τ_i² /2 - C₃ⁱ τi³ / 3, i = 1, …, n.    (30)
Суммарные затраты на выполнение прямого сокращенного метода расчета коэффициентов кубических интерполяционных сплайнов представлены в таблице 2.

Табл. 2. Количество расчетных операций при построении n сплайнов

5. Заключение

Выполненные расчеты трудоемкости алгоритма с применением сплайнов Эрмита и алгоритма прямого частичного расчета коэффициентов кубических интерполяционных сплайнов (таблицы 1 и 2) показывают, что предложенный метод является значительно менее затратным при решении задач управления с прогнозированием.
В сравнении с затратами метода прогонки на построение сплайнов, зависящих от глобальной переменной (что требуется в задаче управления с предсказанием), предложенный метод сокращает число каждой из основных операций примерно в 2 раза.

  
Список литературы:

1.Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2002 г. – 632 с.
2. Гданский Н.И. Геометрическое моделирование и машинная графика. – М.: МГУИЭ, 2003 г. – 236 с.