Построение математической модели котловины Онежского озера

Аннотация

В.Н. Баклагин

Дата поступления статьи: 17.08.2013

Рассмотрен процесс построения математической модели котловины водных объектов. С использованием исходных данных разработана математическая модель котловины Онежского озера. Данная модель может исользоваться при моделировании термических и гидродинамических процессов.

Ключевые слова: Моделирование котловины водных объектов, моделирование термогидродинамики водных объектов, сеточная область, шаг сетки

05.13.18 - Математическое моделирование, численные методы и комплексы программ

В настоящее время математическое моделирование получило очень широкое распространение. Математические модели достаточно часто используются при исследовании свойств объектов различных научных сфер. В частности, в изучении водных объектов математическое моделирование играет не маловажную роль. Математические модели являются одним из основных инструментов количественного и практического регулирования водных экологических систем [1].
В Санкт-Петербургском экономико-математическом институте была разработана трехмерная математическая модель экосистемы Ладожского озера, которая позднее была адаптирована под Онежское озеро. Разработанная модель авторами Л. А. Руховец, В. В. Меншуткин, Г. П. Астраханцев и др, включает трехмерную математическую модель термогидродинамических процессов, переноса примесей и моделей экосистемы больших стратифицированных озер [2-6].
При реализации диагностических и прогностических моделей водных объектов в целом, воспроизводства гидродинамических и термических полей важным фактором является учет особенностей котловины изучаемого водного объекта (батиметрия, рельеф дна). Поэтому возникла необходимость разработать математическую модель котловины Онежского озера, которая не просто дает математическое описание рельефа дна, береговой линии и т.д., а также адаптирована к уже разработанной трехмерной модели Онежского озера.
Как правило, трехмерные математические модели котловин водных объектов представлены в виде трехмерной сеточной области, которая имеет некую дробность – шаги по осям (двум горизонтальным и одной вертикальной оси). Сеточная область характеризуется размерами по трем осям, а также однородностью или неоднородностью [7-10].
Для Онежского озера выбран горизонтальный шаг сетки, равный 1000 метров, что даст вполне адекватное математическое описание котловины озера. По вертикали сеточная область не однородна. Размер сеточной области по оси z составляет 27 узлов, а шаг варьируется от 1 до 20 метров – чем глубже узлы сеточной области, тем больше расстояние между ними.
Исходными данными для построения математической модели котловины Онежского озера являются данные по глубинам в каждом узле двумерной горизонтальной сеточной области:
,     (1)
где  – глубина на пересечении i-ой и j-ой линии двумерной горизонтальной сеточной области. Если узел выходит за пределы береговой линии, то , в противном случае узел характеризуется определенной глубиной.
Для получения трехмерной сеточной области, которая необходима для процессов моделирования термогидродинамики водоема, необходимо перейти от двумерной сеточной области глубин к трехмерной сеточной области, которая имеет бинарную разметку (если узел попадает в водное пространство котловины, то ему присваивается значение 1, в противном случае – 0):
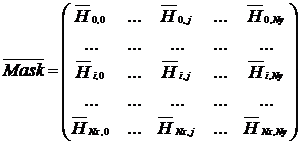,         (2)
где  – матрица, математически описывающая озерное пространство по глубине на пересечении i-ой и j-ой линий трехмерной сеточной области. Математически матрица представлена как:
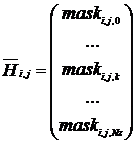,    (3)
где – узел трехмерной сеточной области, который имеет бинарную разметку.
Значение бинарной разметки узла определяется по простому алгоритму, блок-схема которого представлена на рис.1.

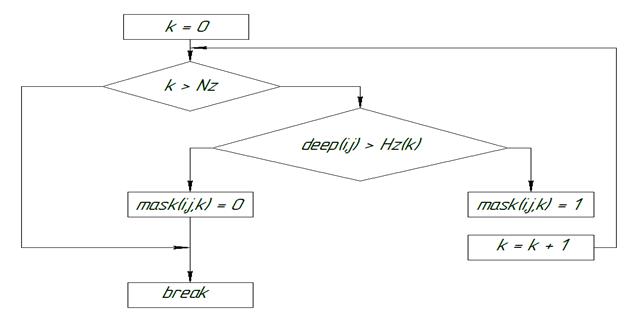
Рис. 1. Блок-схема заполнения узлов трехмерной сеточной области озера бинарными значениями.

Полученной трехмерной матрицы не достаточно для полного описания водного пространства котловины в целях моделирования термогидродинамических процессов, поскольку для расчетов необходимо выполнять условия неразрывности узлов сеточной области. Аналитически это условие можно записать в виде:
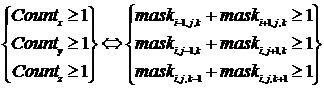.     (4)
Для устранения узлов, которые не удовлетворяют условию (4), разработан алгоритм, вследствие чего происходит сглаживание поверхности дня котловины. Таким образом, достигается возможность моделировать процессы термогидродинамики для исследуемых водоемов.
На основе исходных данных с использованием алгоритмических конструкций для Онежского озера сделаны необходимые расчеты и получены данные, которые математически описывают котловину озера. Эти данные могут использоваться для моделирования термических и гидродинамических процессов Онежского озера. Визуализация данных представлена на рис.2.

Рис. 2. Трехмерная модель котловины Онежского озера.

Список литературы:

1. Зерщикова М. А. Формирование механизма эколого-инновационной деятельности в регионе [Электронный ресурс] // «Инженерный вестник Дона», 2011, № 1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2011/322 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Астраханцев Г. П., Меншуткин В. В., Петрова Н А., Руховец Л. А.. Моделирование экосистем больших стратифицированных озер [Текст]. – СПб.: Наука, 2003 – 363 с.
3. Астраханцев Г. П., Егорова Н. Б., Руховец Л. А. Численное моделирование круглогодичной циркуляции глубоких озер [Текст] / ДАН СССР, 1987 – № 6 –– С.1331-1334.
4. Руховец Л. А., Астраханцев Г. П., Мальгин А. Н., Полосков В. Н., Тержевик А. Ю., Филатов Н. Н. Моделирование климатической циркуляции Онежского озера [Текст] / Водные ресурсы. Т. 33, № 5, 2006. C. 555-566.
5. Меншуткин В. В., Воробьева О. Н. Модель экосистемы Ладожского озера [Текст] / Современное состояние экосистемы Ладожского озера. Л.: Наука, 1987 – С. 187-200.
6. Полосков В. Н.Математические модели для расчета распространения загрязнений в Ладожском озере и их использование для решения природоохранных задач [Текст] // Математические модели для использования экономических механизмов в задачах сохранения водных ресурсов больших озер. Часть 2. СПб: СПб ЭМИ РАН, 2000 – С. 21-32.
7. Ким В. Б., Прокопенко Е. В. Сплайновый подход к моделированию рельефа [Текст] // «Вестник Кемеровского государственного университета», 2009 – № 4 – С. 46-50.
8. Проценко Е. А. Двумерная конечно-разностная модель формирования наносов в прибрежной зоне водоема и ее программная реализация [Электронный ресурс] // «Инженерный вестник Дона», 2010, № 3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2010/224 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Lesley J. P Topographical models or relief-maps // Science, 1886 – Vol. ns-7 – № 154. – P. 58-58.
10. King F. H. Topographical models or relief-maps // Science, 1886 – Vol. ns-7. – № 157. P. 120-121.