О коэффициенте призменной прочности высокопрочных бетонов
Аннотация
Дата поступления статьи: 25.08.2013В статье изучается зависимость отношения призменной прочности (Rb) от кубиковой (R) для высокопрочных бетонов классов В70…В110. Выполнены эксперименты на бетонных кубах с ребром 150 мм и призмах с основанием 150x150 мм и высотой 600 мм. Установлена тенденция к снижению отношения Rb/R с ростом прочности бетона. Предложена новая зависимость Rb=f(R), обеспечивающая более чем 99 %-ную сходимость с экспериментом.
Ключевые слова: высокопрочный бетон, физический эксперимент, призменная прочность, кубиковая прочность, коэффициент призменной прочности
В российской литературе [1] коэффициент призменной прочности, равный соотношению между призменной прочностью (Rb) и кубиковой (R) для бетонов средней прочности рекомендуется определять по следующей формуле:
Rb/R=(0,77-0,00125∙R). (1)
Зависимость (1) апробирована и подтверждена многочисленными экспериментами на бетонах средней прочности – классов до В40…В50. Возможность использования этой зависимости для высокопрочных бетонов классов В70…В120 не исследована [2, 3, 4].
В Еврокоде [4] для таких классов бетона приведен постоянный коэффициент равный 0,8. В работах О.Я. Берга [5] указывается, что зависимость Rb=f(R) носит линейный характер. Для тяжелых бетонов, включая высокопрочные, соотношение Rb/R рекомендуется принимать постоянным, равным 0,783.
С целью изучения свойств высокопрочных бетонов, включая соотношение кубиковой и призменной прочности, был поставлен ряд экспериментов по изучению работы бетонных кубов и призм на центральное сжатие под действием кратковременной нагрузки [6, 7]. Эксперименты проводились в соответствии с требованиями ГОСТ [8, 9] в гидравлическом 250-тонном прессе.
Испытывались стандартные бетонные кубы с размерами грани 150 мм и призмы 150х150х600 мм. Были исследованы бетоны классов В70, В80, В90, В100, В110, изготовленные на материалах Республики Армения. В качестве крупного заполнителя применялся базальтовый щебень фракции 5-20 мм, мелкий заполнитель – кварцевый песок с модулем крупности 3,1. Заполнители применялись промытые и высушенные.
Для приготовления высокопрочного бетона использовался бездобавочный портландцемент марки М500. Производитель – ЗАО “Мика-Цемент” (Mika-Cement, The Armenian Republic). Для обеспечения подвижности смеси при водоцементном отношении В/Ц=(0,2…0,25) в смесь вводился суперпластификатор Mapefluid N200 производства компании Mapei S.p.A., Italy [10] в количестве от 0,5 до 1,0 % от массы цемента.
Средние экспериментальные значения прочности кубов и призм для исследуемых бетонов приведены в таблице № 1. В ней данные опытов дополнены вычисленными значениями коэффициента призменной прочности и их сопоставлением с экспериментом. На рис. 1 в графическом виде показана экспериментальная зависимость призменной прочности от кубиковой, Rb=f(R) для полученных высокопрочных бетонов.
Полученные экспериментальные значения коэффициента призменной прочности 0,769…0,788 (таблица №1) достаточно хорошо согласуются с предложенным О.Я. Бергом значением 0,783, независящим от прочности бетона. Максимальная разница составляет 1,8 % для бетона В96. Однако в эксперименте выявлена явная тенденция к снижению исследуемого коэффициента с ростом прочности бетона, поэтому принятие постоянного значения коэффициента призменной прочности для бетонов различных классов проведенными экспериментами не подтверждено.
Таблица № 1
Соотношение призменной и кубковой прочности бетонов
Класс бетона |
Кубиковая, R, и призменная, Rb, прочность бетона, МПа |
Отношение Rb/R |
Среднее отклонение экспериментальных данных от: |
|||||
|
вычисленных по (1) |
вычисленных по предложению (2) |
|||||||
|
R |
Rb (15x15x60) |
экс-перимент |
по (1) |
абсолютное |
относительное, % |
абсолютное |
относительное, % |
|
|
B62 |
63,5 |
50,1 |
0,788 |
0,691 |
0,097 |
14,1 |
-0,0004 |
-0,001 |
|
B70 |
71,4 |
56,1 |
0,786 |
0,681 |
0,105 |
15,5 |
0,0005 |
0,001 |
|
B81 |
84,7 |
66,2 |
0,782 |
0,664 |
0,118 |
17,7 |
0,0013 |
0,002 |
|
B89 |
93,2 |
72,4 |
0,777 |
0,654 |
0,123 |
18,9 |
-0,0006 |
-0,001 |
|
B96 |
97,6 |
75,1 |
0,769 |
0,648 |
0,121 |
18,7 |
-0,0070 |
-0,009 |
|
B107 |
108,4 |
83,7 |
0,772 |
0,634 |
0,138 |
21,7 |
-0,0001 |
0,000 |
Анализируя данные таблицы №1 можно увидеть, что экспериментальные значения коэффициента призменной прочности не соответствуют значениям, полученным по формуле (1). Отклонение экспериментальных значений от полученных по формуле (1) составляет от 14 до 22%, причём отклонение увеличивается с ростом класса бетона. Из этого следует, что зависимость (1) не отражает особенностей высокопрочных бетонов и необходима ее корректировка.
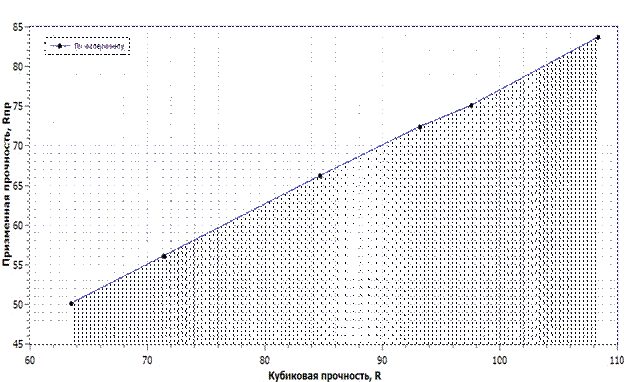
Рис. 1.- Зависимость призменной прочности от кубиковой
Учитывая полученную экспериментальную зависимость коэффициента призменной прочности от кубиковой прочности, предлагается следующий откорректированный вид зависимости Rb=f(R), обеспечивающий совпадение с экспериментальными данными более чем на 99% (см. таблицу №1):
Rb =(0,77∙b -0,00125R)R, (2)
где b =1,123+0,00115(R-60); R≥60 МПа.
На рис. 2 представлен график зависимости коэффициента призменной прочности от кубиковой прочности, Rb/R=f(R), на основе данных эксперимента, полученный из формул (1), (2), принятый в еврокоде и по предложению О.Я. Берга.
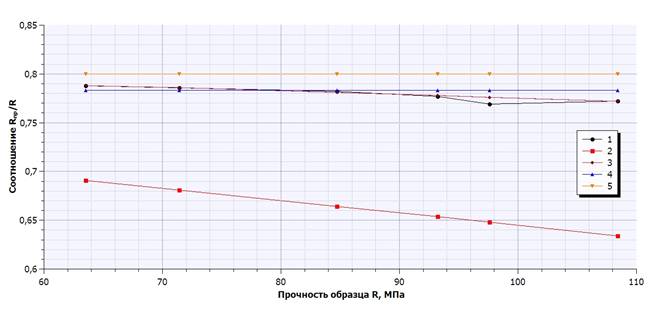
Рис. 2.- Зависимость коэффициента призменной прочности от прочности образца: 1 – по данным эксперимента; 2 – по стандартной формуле (1); 3 – по предложенной формуле (2) 4 – по предложению О.Я. Берга; 5 – по еврокоду [4].
Как видно из рис.2, предложенная формула (2), даёт очень близкий результат с экспериментальными данными. Она учитывает снижение коэффициента призменной прочности с повышением класса бетона. Таким образом, зависимость призменной прочности высокопрочных бетонов классов В70…В110 от кубиковой рекомендуется определять по формуле (2).
Литература:
1. СНиП 2.03.01-84*. Бетонные и железобетонные конструкции [Текст].– Введ. 1986-01-01. –М.: Госстрой СССР, 1985. – 80 с.
2. Несветаев, Г.В. Бетоны: учебное пособие [Текст] / Г.В. Несветаев. – Ростов н/Д: Феникс, 2011. – 381 с.
3. El-mahadi, A. Rheological Properties, Loss of Workability and Strength Development of High-Strength Concrete [Текст] / El-mahadi Ahmed.– London: MSc. University of London, 2002. – 144 р.
4. EN 1992 Eurocode 2: Design of concrete structures. Part 1: General rules and rules for buildings [Текст]. – Brussels: European Committee for Standardization, 2001. – 52 р.
5. Берг, О.Я. Высокопрочный бетон [Текст] / О.Я. Берг, Е.Н. Щербаков, Г.Н. Писанко.– М.: Стройиздат, 1971. – 207 с.
6. Кургин, К.В., Маилян Д.Р. О необходимости трансформации базовой аналитической зависимости "sb–eb" бетона. [Электронный ресурс] // «Инженерный вестник Дона», 2011, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2011/712 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Маилян, Д.Р., Несветаев, Г.В. Зависимость относительной несущей способности колонн от относительного эксцентриситета. [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1334 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. ГОСТ 10180-90. Бетоны. Методы определения прочности по контрольным образцам [Текст].– Введ. 1991-01-01.–М.: ФГУП «Стандартинформ», 2006. –30 с.
9. ГОСТ 24452-80. Бетоны. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона [Текст].– Введ. 1982-01-01.–М.: ФГУП «Стандартинформ», 2005. –12 с.
10. Mapei Mapefluid N200. – Mapei S.p.A., Italy: [Электронный ресурс]. [2013]. URL: http://www.mapei.com/public/COM/products/704_GB.pdf
11. Metin Husem, Selim Pul. Investigation of stress–strain models for confined high strength concrete // “Sadhana” Vol. 32, Part 3, June 2007, pp. 243–252. India.
12. Тер-Петросян П.А. Материаловедение для строителей (руководство) / П.А.Тер-Петросян, А.М. Асирян, Э.А. Мовсисян, Г.В. Ованнисян, Д.Н. Ованнисян, Э.Р. Саакян, В.В. Петросян. Ереван: Наири, 2005. 616 с.