Расчет оптимальной величины защитного слоя бетона колонн квадратного сечения

Аннотация

В.А. Мурадян

Дата поступления статьи: 25.09.2013

Предлагается подход к расчету оптимальных значений защитного слоя бетона продольно армированных колонн, работающих при центральном сжатии. Моделирование осуществлено с использованием МКЭ - пакета  Ansys при реализации пространственной конструкции и плоской модели сечения колонны. 

Ключевые слова: железобетонная колонна, продольная арматура, защитный слой бетона, метод конечных элементов, критическая нагрузка

Предлагается подход к расчету оптимальных значений защитного слоя бетона продольно армированных колонн, работающих при центральном сжатии. Моделирование осуществлено с использованием МКЭ - пакета  Ansys при реализации пространственной конструкции и плоской модели сечения колонны.
Ряд исследований по расчету железобетонных колонн при центральном и внецентренном сжатии показал существенное включение в работу конструкции ее центральной части, в особенности при нагрузках, близких к критическим [1-6]. При этом, основываясь на анализе пространственной конечно-элементной модели колонны прямоугольного сечения с продольным армированием при центральном сжатии по характеру поведения главных напряжений  и , параллельных плоскости нормального сечения колонны, убеждаемся, что сечения в средней части колонны подвержены деформации растяжения. Характер распределения интенсивности напряжений в центральной части колонны является достаточно однородным, однако уровень напряжений зависит от положения вертикальной арматуры по сечению [7].  Это позволяет сделать вывод о возможности исследования критических усилий, воспринимаемых конструкцией, на основе анализа напряженно-деформированного стояния в плоскости центральных сечений.
Рассмотрим конечно-элементную модель плоского деформирования нормального сечения колонны  в следующей постановке [8-10]:
,    ,
где  - область, занимаемая бетоном, - область арматуры (рис. 1),
 - величина защитного слоя бетона.
На линиях  задаются нормальные растягивающие распределенные усилия по закону   и  соответственно. На линиях ,    - условия симметрии деформирования сечения колонны:
,  .

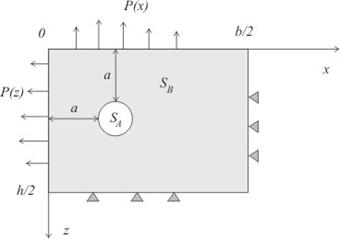
Рис. 1

В качестве физических параметров выбраны значения величин, представленных в таблице 1, и использованных как для пространственной, так и плоской моделей.
Таблица 1

Для плоской модели сечения считаем уровень прикладываемых нагрузок соответствующим линейному участку деформирования среды без учета пластических деформаций  и процессов трещинообразования.     Исходя из  этого, при реализации МКЭ модели сечения использованы плоские 8-узловые элементы Plane82 [8] с двумя поступательными степенями свободы в каждом узле. Характер разбиения сечения конечными элементами представлен  на рис. 2 с использованием локальной системы координат  и зеркальном отражении области  для полного представления сечения колонны.

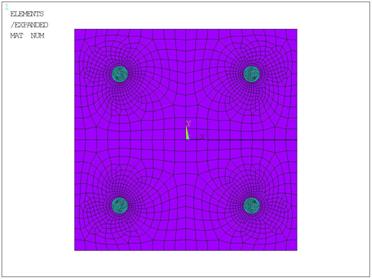
Рис. 2 Сетка конечных элементов

Для выбора характера прикладываемой нагрузки  рассмотрены перемещения в среднем сечении колонны пространственной модели при уровне вертикального сжимающего усилия 0.7 от  критического. Модуль вектора перемещений в сечении близок аналогичной величине смещения при плоской деформации при равномерном распределении нагрузки . Близость диаграмм распределения перемещений по сечению позволила сделать вывод о возможности рассмотрения случая постоянных усилий .
Дальнейшее исследование по выбору оптимального положения арматуры по сечению колонны основывалось на анализе  интенсивности напряжений  в зависимости от величины защитного слоя бетона  
.
В качестве основного варианта использован случай выбора геометрических параметров модели:  м. Установлено, что основными влияющими факторами на распределение интенсивности напряжений в сечении являются: соотношение модулей упругости бетона и арматуры,  а также коэффициент Пуассона бетона, в основном определяющий  характер сжимаемости материала сечения.
Установлено, что наиболее чувствительной характеристикой к изменению положения арматуры является концентрация напряжений вблизи границы раздела арматуры и бетона. Величина , Па  на поверхности арматуры от параметра , м выведена на рис. 3.

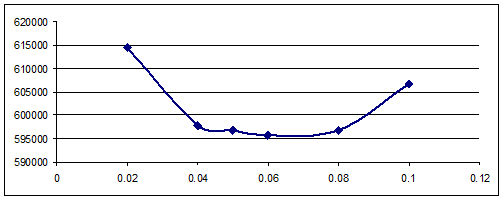
Рис. 3. Распределение , Па от параметра .

Отметим, что минимальное значение полученной характеристики соответствует значению м и по сути определяет максимальный уровень критического усилия, приводящего к разрушению конструкции. Полученное значение соответствует анализу задачи  в пространственной постановке по расчету критических усилий при нелинейном деформировании среды с учетом явлений трещинообразования и дробления бетона.

Литература:

1. Мурадян В.А., Маилян Д.Р. Железобетонные стойки с заглубленными продольными стержнями без поперечного армирования // Расчет и проектирование железобетонных конструкций. - Ростов-на-Дону: РГСУ, 2009 – С. 94-95.
2. Мурадян В.А., Маилян Д.Р. Устойчивость арматурных стержней в сжатой железобетонной колонне // Строительство 2010. Материалы научно-практической конференции. - Ростов-на-Дону: 2010 . – С.40-42.
3. Кургин К.В., Маилян Д.Р. Работа керамзитофибробетонных колонн при повторных нагрузках [Электронный ресурс]  // «Инженерный вестник Дона», 2012,  №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2012/738 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Мурадян В.А., Маилян Д.Р. К методике расчета железобетонных внецентренно сжатых колонн // «Инженерный вестник Дона», 2012, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1333 (доступ свободный) – Загл. с экрана. – Яз. рус.
5. Маилян Д.Р., Несветаев Г.В. О несущей способности колонн из высокопрочных самоуплотняющихся бетонов // Бетон и железобетон в третьем тысячелетии. Материалы научно-практической конференции. - Махачкала: 2010. – С.47-49.
6. Маилян Д.Р., Резван И.В. Несущая способность бетонного ядра трубобетонных колонн // Вестник Майкопского государственного технического университета. -Майкоп: 2011. – С. 14-19.
7. Шиляева О.В., Хунагов Р.А.,  Блягоз А.М.   Моделирование устойчивости железобетонной панели      // Новые технологии. - 2012. – Вып. 3. – С. 114-119.
8. ANSYS, Inc. Theory Reference: ANSYS Release 9.0. – С.14-203.
9. Mkrtchyan A., Akcenov V., Mailyan. Experimental study of the structural properties of high-strength concrete // 5th International Scientific Conference “European Applied Sciences: modern approaches in scientific researches”:Papers of the 5th International Scientific Conference. August 26–27. - Stuttgart, Germany. – 2013.  - 164 p.
10. Mkrtchyan A., Akcenov V., Mailyan. Experimental study of reinforced concrete columns of high-strength concrete // “Applied Sciences and technologies in the United States and Europe: common challenges and scientific findings”: Papers of the 2nd International Scientific Conference (September 9–10, 2013). Cibunet Publishing. - New York, USA. - 2013. - 242 p.