Оптимизация толстостенной железобетонной оболочки на основе решения обратной задачи механики неоднородных тел
Аннотация
Дата поступления статьи: 25.09.2013Решена задача оптимизации толстостенного предварительно напряженного железобетонного цилиндра, нагруженного внутренним давлением. Предварительные напряжения в таком цилиндре создаются намоткой с натягом тросов по внешней поверхности. Идея метода заключается в отыскании закона изменения модуля упругости, при котором напряженное состояние равно заданному. Получена аналитически зависимость модуля упругости от радиуса, при которой по всей толщине оболочки не возникает растягивающих напряжений. Создание косвенной неоднородности позволило уменьшить расход арматуры на 10%. Также была решена и прямая задача - определение напряженно-деформированного состояния для цилиндра с постоянным модулем упругости.
Ключевые слова: толстостенный предварительно напряженный железобетонный цилиндр, оптимизация, обратная задача, теория упругости, неоднородность
В настоящее время толстостенные оболочки находят широкое применение в конструкциях радиационно-тепловых экранов ядерных реакторов, тепловых и биологических защит и т.д. Вопросам оптимизации таких оболочек, а также других конструкций, посвящены работы[1-10]. Все указанные работы базируются на идеях академика РААСН В.И. Андреева[1].
Известно, что если в некоторой области конструкции уменьшить модуль упругости, то и напряжения в этой области уменьшатся[1,2]. Таким образом, варьируя модуль упругости, можно добиться, чтобы напряжения во всех точках конструкции были постоянны.
Рассмотрим способ оптимизации на примере толстостенной предварительно напряженной железобетонной цилиндрической оболочки, нагруженной внутренним давлением pa. Предварительные напряжения в таких конструкциях, как правило, создаются намоткой с натягом тросов по внешней поверхности. Решим сначала прямую задачу: определим, какие напряжения будут возникать в толще конструкции, если модуль упругости бетона постоянен. Расчетная схема оболочки представлена на рис. 1. Действие арматуры заменяем внешним контактным давлением pb.
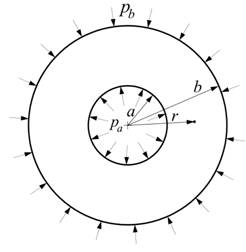
Рис.1. Расчетная схема оболочки.
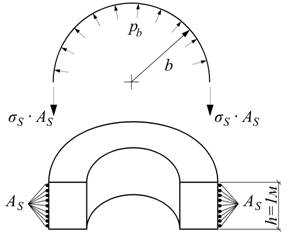
Рис. 2. К определению давления pb.
Будем считать, что цилиндр достаточно длинный, т.е. он находится в условиях плоской деформации (![]() ).Величину
).Величину ![]() можно определить из условия равновесия его половины (рис.2).
можно определить из условия равновесия его половины (рис.2).
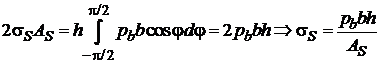 (1) (1) |
|
Напряжения в кольцевой арматуре определяются выражением:
|
|
где ![]() - начальные напряжения в кольцевой арматуре (до момента передачи усилий на бетон).
- начальные напряжения в кольцевой арматуре (до момента передачи усилий на бетон).
Из решения задачи Ляме для случая плоской деформации известна формула для перемещений ![]()
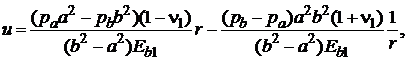 (3) (3) |
|
где 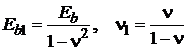 .
.
Тогда выражение для окружной деформации можно записать в виде:
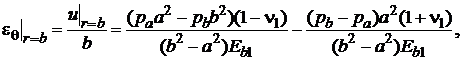 (4) (4) |
|
Подставив выражения (4) и (1) в (2), после некоторых преобразований получим формулу для контактного давления:
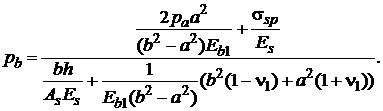 (5) (5) |
|
Далее, чтобы определить напряжения ![]() и
и ![]() в бетоне, нужно подставить значение
в бетоне, нужно подставить значение ![]() в известные формулы для задачи Ляме.
в известные формулы для задачи Ляме.
На рис. 3 показан график распределения напряжений ![]() при pa=10МПа,
при pa=10МПа, ![]()
![]() =500 МПа.
=500 МПа.
Чтобы не возникало растягивающих напряжений, для рассматриваемого примера потребовалось 1622 кг арматуры на 1 метр длины трубы. Как видно из графика, ![]() только при
только при ![]() , т.е. предельное состояние в этом случае наступает только у внутренней поверхности.
, т.е. предельное состояние в этом случае наступает только у внутренней поверхности.
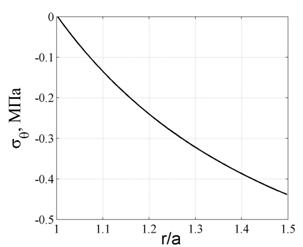
Рис. 3. График распределения напряжений
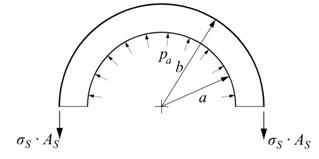
Рис. 4. Равновесие отсеченной половины оболочки
Найдем такое распределение модуля упругости, при котором ![]() во всей толще цилиндра. Рассмотрим равновесие его половины (рис. 4).
во всей толще цилиндра. Рассмотрим равновесие его половины (рис. 4).
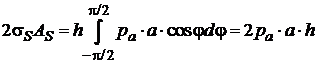
Но из (1): ![]() . Тогда
. Тогда ![]() . Зависимость модуля упругости, при которой
. Зависимость модуля упругости, при которой ![]() во всей толще цилиндра, нагруженного внутренним давлением
во всей толще цилиндра, нагруженного внутренним давлением ![]() и внешним давлением
и внешним давлением ![]() имеет вид[1]:
имеет вид[1]:
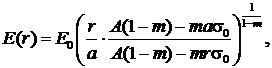 (6) (6) |
|
где ![]() .
.
Подставив ![]() в (6), получим:
в (6), получим: ![]() .
.
Остается определить требуемую площадь арматуры, при которой ![]() .
.
|
|
Окружную деформацию бетона на внешней поверхности можно найти следующим образом:
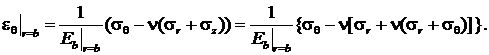
С учетом того, что ![]() , а
, а ![]() , получим:
, получим:
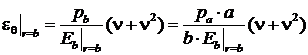 (8) (8) |
|
Подставив (8) в (7), получим требуемую площадь арматуры:
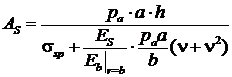 . (9) . (9) |
|
На рис. 5. представлена кривая ![]() для оптимального цилиндра. Исходные данные были взяты те же, что и для однородной оболочки.
для оптимального цилиндра. Исходные данные были взяты те же, что и для однородной оболочки.
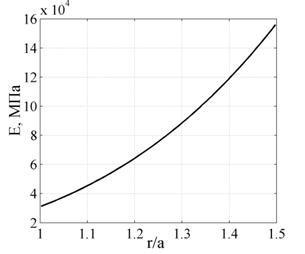
Рис. 5. График зависимости ![]() для оптимального цилиндра
для оптимального цилиндра
Для неоднородного цилиндра потребовалось 1473 кг арматуры на 1 м длины трубы. Экономия арматуры при создании искусственной неоднородности составила 10.1%.
Литература:
- Андреев В.И. Потехин И.А. Оптимизация по прочности толстостенных оболочек: монография. М.:МГСУ, 2011. – 86с.
- Андреев В.И. Некоторые задачи и методы механики неоднородных тел: монография. – М.: Издательство АСВ, 2002. – 288 с.
- Потехин И.А. Способ оптимизации конструкций на основе решения обратных задач теории упругости неоднородных тел. Дисс. канд. техн. наук. М., 2009. - 144 с.
- Andreev V.I. About one way of optimization of the thick-walled shells. Applied Mechanics and Materials, Vols.166-169 (2012) pp. 354-358
- Андреев В.И., Булушев С.В. Оптимизация неоднородной толстостенной сферической оболочки, находящейся в температурном поле. Вестник МГСУ, 2012, №12, стр. 40-46.
- Andreev V.I. Optimization of thick-walled shells based on solutions of inverse problems of the elastic theory for inhomogeneous bodies. Computer Aided Optimum Design in Engineering XII (OPTI XII). WIT Press. 2012, p.189-201
- Чепурненко А.С., Андреев В.И., Языев Б.М. Построение модели равнопрочной многопролетной балки [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1571 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Чепурненко А.С., Языев Б.М. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости//Научное обозрение. 2012. № 6. — С. 202-204.
- Чепурненко А.С., Андреев В.И., Языев Б.М. Построение модели равнонапряженного цилиндра на основе теории прочности Мора //Вестник МГСУ. №5 2013, с.56-61.
- Козельская М.Ю., Чепурненко А.С., Литвинов С.В. Применение метода Галёркина при расчете на устойчивость сжатых стержней с учетом ползучести [Электронный ресурс] // «Инженерный вестник Дона», 2013, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2013/1714 (доступ свободный) – Загл. с экрана. – Яз. рус.