Инструментальные средства поддержки процесса моделирования, основанного на L-системах

Аннотация

Федотов П.В., Ильичева О.А.

Предлагается программно-технологический комплекс для обеспечения моделирования, использующий в качестве инструмента построения моделей и визуализации результатов L-системы (системы Линденмайера). Основное предназначение ¬¬¬– построение моделей процессов и структур, имеющих фрактальную природу. Комплекс поддерживает работу с различными типами L-систем: детерминированными контекстно-независимыми, стохастическими, параметрическими, контекстно-зависимыми. Разработанная система использовалась для моделирования и анализа социально-экономических процессов.

Ключевые слова: L-системы, Моделирование, Фракталы, Самоподобные структуры, Правила порождения, Грамматика, Графическая интерпретация

05.13.17 - Теоретические основы информатики

L-системой (L-system, LindenmayerSystem) называют предложенную АристидомЛинденмайером математическую модель – разновидность формальной порождающей грамматики с механизмом визуализации, которая изначально применяласьдля изучения процесса роста и развития растений и простейших организмов[1].В настоящее время
L-системы с различными расширениями применяются для моделирования сложных ветвящихся структур и процессов.

Грамматика системы состоит из алфавита, стартовой аксиомы-инициализатора и набора порождающих правил. К строке аксиомы на каждом шаге одновременно применяются все подходящие правила порождения. Процесс эволюции – разрастания бесконечен, поэтому число итераций каким-либо образом ограничивается. Механизм визуализации результата отделен от части, отвечающей за генерацию новой строки, и применяется по завершении вывода по грамматике.

Наиболее простым вариантом является детерминированная контекстно-независимая L-система: результирующая строка для заданных аксиомы и количества итераций всегда одинакова. Существуют и иные варианты системы, расширяющие её возможности: стохастические (правила порождения применяются с вероятностью; наличие конкурирующих правил), контекстно-зависимые (выбор правила порождения для конкретного символа зависит от его окружения – контекста), параметрические (передача численных параметров, которые могут влиять как на вывод, так и на визуализацию) L-системы.

В последнее время применение L-систем получило особую актуальность для построения фрактальных объектов. Теория фракталов нашла широкое применение в физике, астрономии, биологии, а также и в экономических науках, в частности для анализа финансовых рынков. С точки зрения этих приложений использование фракталов рассматривается как наиболее перспективное современное направление математики. В более широком смысле фрактальность представляют как механизм эволюции живого и неживого. Свойство бесконечного порождения самоподобных структур затрагивает также и социально-экономические процессы[2]. В частности, фрактальностью обладают, как представляется, и процессы распространения таких явлений, как коррупция, что находит отражение в соответствующих моделях.

В настоящей работе реализован общий аппарат L-системы с порождением строк и их визуализацией. Предусмотрена возможность задания любого из трёх видов L-систем: детерминированного, стохастического, параметрического, контекстно-зависимого вывода. Разработанный комплекс позволяет задавать модель в виде L-системы (аксиому, правила порождения, вероятности, параметры), а также глобальные (для нескольких моделей) и локальные (для одной модели) параметры интерпретатора результатов моделирования, реализующего визуализацию. Система дополнена функцией «памяти» – запись параметров в строку порождения. Эта функция используется, если L-система стохастическаяи случайные параметры должны применяться только к новому генерируемому уровню, оставляя все предыдущие без изменения.

Например, для порождения классической фрактальной фигуры «Снежинка Коха» необходимо задать в качестве входных данных аксиому F++F++F, правило порождения F→F–F++F–F, угол поворота 60^°. Эта фигура задается детерминированной контекстно-независимой L-системой. В предлагаемом подходе разработано пользовательское приложение, позволяющее задавать всю необходимую информацию о модели и отображать результат её работы  (Рис. 1).

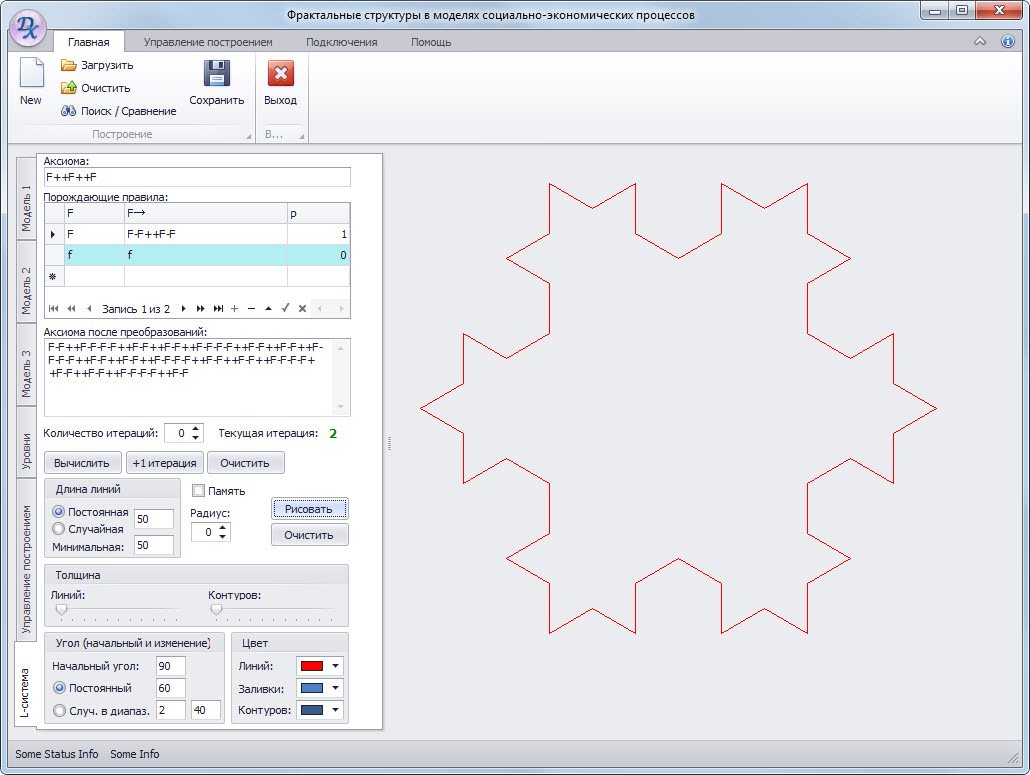
Рис. 1 Снежинка Коха после трех итераций

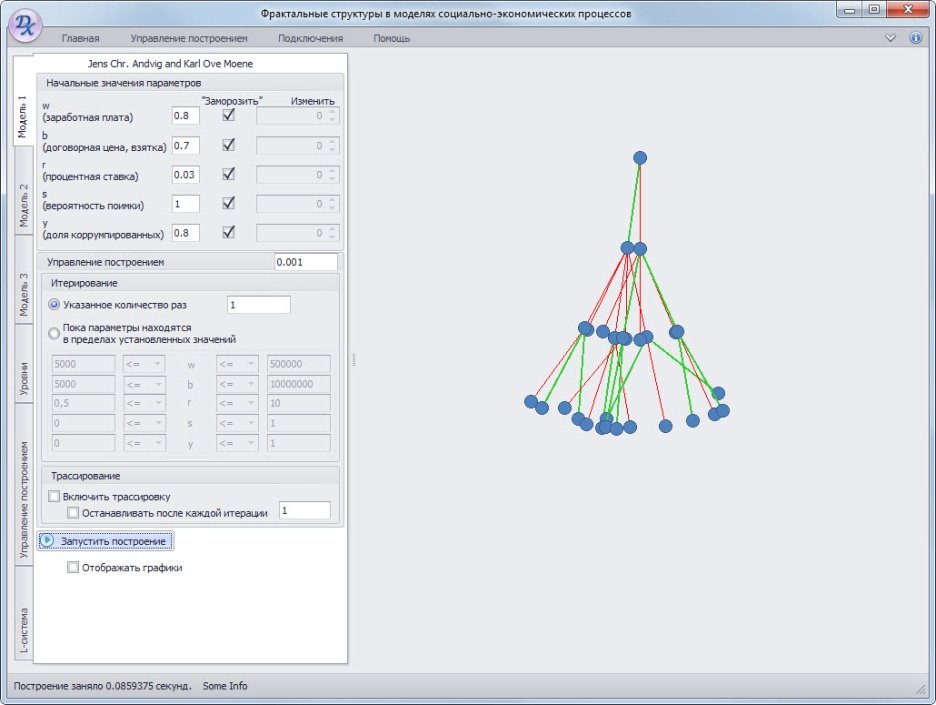Для иллюстрации стохастической параметрической модели рассмотрены L-системы, построенные в результате анализа, проведенного автором[3], некоторых известных моделей коррупции. Выяснилось, что основные уравнения этих моделей фактически задают механизм порождения самоподобных структур. Так, например, модель [4], уравнения которой служили основой для построения правил в стохастической параметрической L-системе, демонстрирует в динамике процесс заражения коррупцией, представленный на рисунках рис.2,рис.3.
Рис. 2 Развитие коррупционного процесса в модели Андвига-Моене, третья итерация

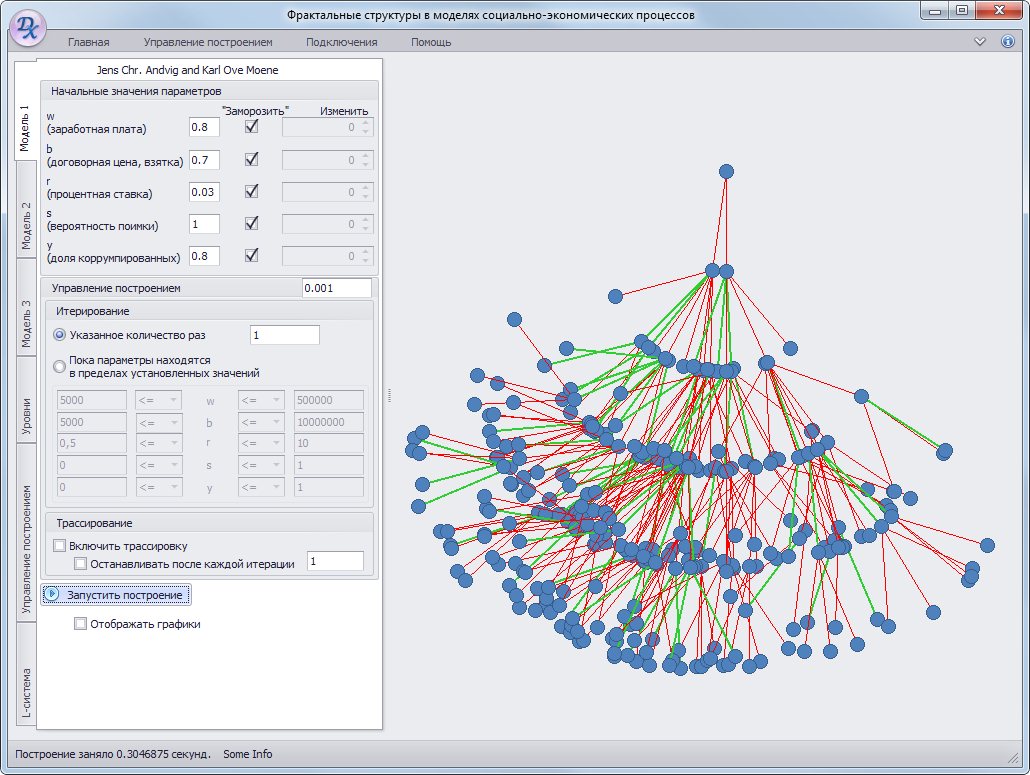
Рис. 3 Развитие коррупционного процесса в модели Андвига-Моене, десятая итерация

L-система, соответствующая этой модели, включает несколько правил, в которых отражены y(t) – доля коррумпированных бюрократов в момент времени t, s – вероятность поимки, b – договорная цена (размер взятки), w – заработная плата, r – процентная ставка на текущий период.

Перечисленные параметры влияют на визуализатор: длину, толщину и цвет отрезков, диаметр окружностей, процент окружностей, имеющих потомков.Цвет линий отражает причину вовлечения в коррупционный акт (снижение заработной платы, например, окрашивает отрезок в зелёный цвет). Графический интерпретатор L-системы реагирует на изменение параметров исследуемой модели. Реализован интерфейс для задания контекстно-зависимых параметров.Кроме того, предусмотрена возможность пользовательского задания интерпретации параметров, как с помощью специального меню, так и подключением собственных программных модулей.

Визуализация процесса распространения коррупции наглядно демонстрирует его фрактальную природу. В процесс вовлекается всё большее количество участников (представлены визуализатором окружностями) и связей между ними (коррупционные акты).При этом порождаемые структуры являются самоподобными.

Похожую картину даёт представленная с помощью L-систем модель коррупции Ф.Луи [5].Основные параметры, влияющие на вывод грамматики и затем на визуальное отображение: p(t) – вероятность поимки коррупционера во время t; p(t-1) – вероятность поимки во время t-1; p^e(t) – вероятность поимки во время t, ожидаемая в период t-1; p^e(t+1) – вероятность поимки во время t+1, ожидаемая в период t; C – штраф.

Один из вариантов визуализации второй модели показан на рис.4.Красные окружности представляют поколение «старых» бюрократов, белые – поколение «молодых», зелёные окружности – пойманные и оштрафованные бюрократы.

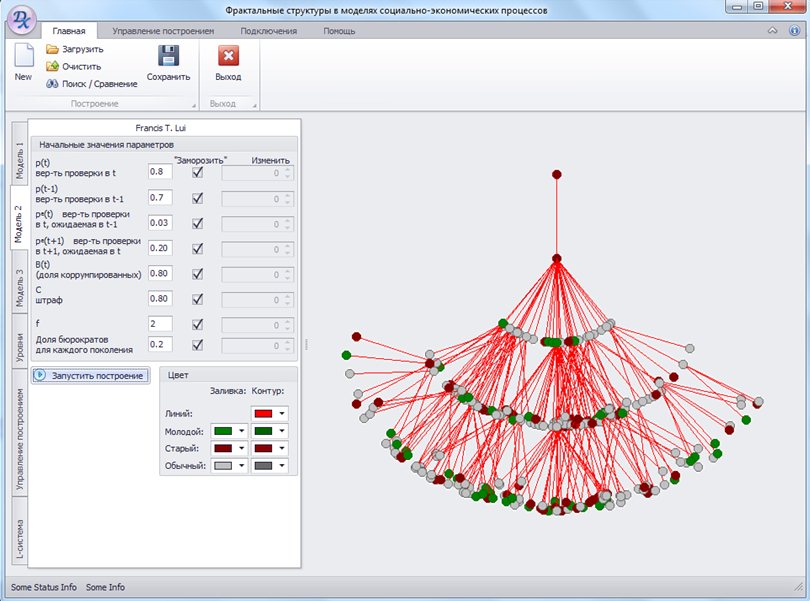
Рис. 4 Визуализация модели Ф.Луи, третья итерация

С точки зрения теории фракталов, результаты приведенного моделирования коррупции могут быть рассмотрены как предфракталы (самоподобие наблюдается только при ограниченном изменении масштаба) или квазифракталы (неполнота и неточность повторения структуры), что бывает характерно для моделей социально-экономических процессов.

Предлагаемый комплекс может быть использован для моделирования различных динамических процессов и структур, представляемых с помощью L-систем.

Литература

1. AristidLindenmayer, PrzemyslawPrusinkiewiczThe Algorithmic Beauty of Plants /Springer-Verlag.– 1996.– 228 pages.

2. МуравьеваМ.П., ЛябахН.Н.Моделированиединамикиизменениясостояниясоциально-экономическихсистем./ ИзвестияТРТУ. Тематический выпуск «Системный анализ в экономике и управлении». – Таганрог: издательство ТРТУ. – 2006. – №17(72). – 406с.

3. Федотов П.В. Имитационная модель коррупционных процессов / Материалы  XXXIX конференции «Математическое моделирование в проблемах рационального природопользования». – Ростов-на-Дону: Издательство Южного федерального университета. – 2011. – 452с.

4. Andvig, Jens Chr., Moene, Karl OveHow corruption may corrupt / Journal of Economic Behavior & Organization.– 1990. – Issue (Month): 1 (January). – Pages: 63-76.

5. Lui, Francis T., A dynamic model of corruption deterrence / Journal of Public Economics.– 1986. – Issue (Month):2 (November). – Pages: 215-236.