Методы математического моделирования при оптимизации параметров энерго-ресурсосбережения стирально–отжимных машин
Аннотация
В данной статье обосновано, что параметром, определяющий энергозатраты процессов стирки, полоскания отжима, является G-фактор. Авторами предложен математический аппарат определения зависимостей технических показателей от G-фактора. Он является индикатором эффективности процесса оптимизации технических решений конструктивного исполнения стирально-отжимных машин и основой фундаментального анализа типовых конструкций.
Ключевые слова: стирально-отжимная машина, математическое моделирование, G-фактор, энергоэффективность, оптимизаия технических решений.
Для прачечного оборудования основными критериями энерго-ресурсосбережения является: расход электроэнергии, воды, СМС на 1 кг стираемых изделий с обеспечением нормируемых показателей качества стирки полоскания и отжима. На этапе проектирования и производства стирально-отжимных машин критериями энерго ресурсосбережения являются массогабаритные и себестоимость её изготовления.
В настоящее время недостаточно точных представлений о путях достижения оптимальных результатов энерго-ресурсосбережения на этапе изготовления и эксплуатации стирально-отжимных машин одновременно по всем вышеперечисленным критериям. В рамках данной статьи авторами рассматривается теоретические основы динамики перемещения изделий из ткани во вращающемся барабане, являющейся основой для математического моделирования процесса восстановления гигиенических и потребительских свойств изделий из ткани.
Известно, что на энерго-ресурсосберегающие процессы стирки влияют многочисленные конструкторско-технологические факторы [1]: геометрические размеры барабана т.е. объём барабана, диаметр и длинна барабана; G-фактор и частота вращения барабана; количество и форма гребней; качество воды (жесткость) и температура моющего раствора; качество моющего средства и его концентрация; временной фактор (длительность стирки и полоскания); структура вращения барабана (реверсивное вращение барабана или безреверсивное вращение барабана, длительность вращения в одну и противоположную сторону и пауза между ними.
Рассмотрим вопросы влияния конструктивно-технологических факторов и способов стирки на функциональные показатели стирально-отжимных машин барабанного типа.
В настоящие время для профессиональных стиральных машин как отечественного так и зарубежного производства важнейшим показателем, определяющим их массогабаритные показатели является объёмный модуль:
![]() 1)
1)
где ![]() – геометрический объём барабана, дм3 ,
– геометрический объём барабана, дм3 , ![]() – загрузочная масса ткани изделий в воздушно сухом состоянии.
– загрузочная масса ткани изделий в воздушно сухом состоянии.
Как правило завод изготовитель выпускает параметрический ряд стиральных машин, определяемой загрузочной массой![]() .
.
Например, ОАО "Вяземский машиностроительный завод" выпускает стирально-отжимные машины с загрузочной массой![]() :7 кг, 10 кг, 15 кг, 20 кг, 30 кг,40 кг, 60 кг. (в перспективе разработка стиральных машин на 75 кг и 100 кг).
:7 кг, 10 кг, 15 кг, 20 кг, 30 кг,40 кг, 60 кг. (в перспективе разработка стиральных машин на 75 кг и 100 кг).
При известной загрузочной массе![]() и объёмном модуле определяется геометрический объём барабана
и объёмном модуле определяется геометрический объём барабана
![]() 2)
2)
где ![]() загрузочная масса изделия в сухом состоянии; М – объёмный модуль это объём барабана приходящийся на 1 кг. загрузочной массы изделий,дм3/кг(M=10 дм3/кг=const);
загрузочная масса изделия в сухом состоянии; М – объёмный модуль это объём барабана приходящийся на 1 кг. загрузочной массы изделий,дм3/кг(M=10 дм3/кг=const);
Далее перед проектировщиком стоит задача рассчитать диаметр и длину барабана, расчётная схема которой представлена на рисунке 1.
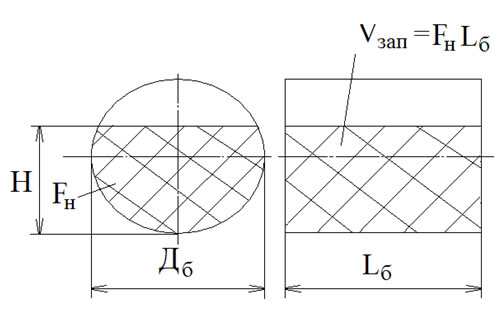
Рис.1.Расчётная схема.
![]() – диаметр барабана;
– диаметр барабана; ![]() – длина барабана;
– длина барабана; ![]() – высота заполнения смоченной тканью изделий загрузочной массой
– высота заполнения смоченной тканью изделий загрузочной массой![]() ;
; ![]() – площадь поперечного заполнения смоченной тканью изделий загрузочной массой
– площадь поперечного заполнения смоченной тканью изделий загрузочной массой![]() ;
; ![]() – объём заполнения смоченной тканью изделий загрузочной массой
– объём заполнения смоченной тканью изделий загрузочной массой ![]() ; – загрузочная масса изделий в воздушно сухом состояния для параметрического ряда для проектируемых машин (7,10,15,18,20,30,40,60,75,100 кг).
; – загрузочная масса изделий в воздушно сухом состояния для параметрического ряда для проектируемых машин (7,10,15,18,20,30,40,60,75,100 кг).
![]()

где ![]() – коэффициент длины барабана.
– коэффициент длины барабана.
Оптимальное значение коэффициента длины барабана характеризуется выражением: 0,618033889, то есть определяется числом золотого сечения.
Степень заполнения объёма барабана смоченной тканью изделий определяется по формуле:
![]() 0,618033889,
0,618033889,
где ![]() – объёмный модуль;
– объёмный модуль; ![]() -удельный объём смоченной ткани изделий (измеряемая величина экспериментально с высокой степенью точности в мерном цилиндре);
-удельный объём смоченной ткани изделий (измеряемая величина экспериментально с высокой степенью точности в мерном цилиндре);
Тогда диаметр барабана определяется по формуле:
где Kc - коэффициент длины барабана определяется по формуле
:![]()
Для оценки интенсивности механического воздействия во время стирки на изделия, такие показатели как загрузочная масса, скорость вращения, частота оборотов барабана недостаточно информативна. Поэтому в таких случаях пользуются обобщенными показателями, например G-фактор (![]() ), который определяет характер и динамику перемещения смоченных тканей изделия во вращающемся барабане, а также качество стирки и качество полоскания. G-фактор (
), который определяет характер и динамику перемещения смоченных тканей изделия во вращающемся барабане, а также качество стирки и качество полоскания. G-фактор (![]() ), определяется отношением центробежного ускорения на внутренней поверхности обечайке барабана к ускорению силы тяжести (g=9.810665 м/) и определяется по формуле:
), определяется отношением центробежного ускорения на внутренней поверхности обечайке барабана к ускорению силы тяжести (g=9.810665 м/) и определяется по формуле:
![]() =
=![]()
![]()
![]()
![]() ,-радиус барабана в м;.
,-радиус барабана в м;.
![]()
![]() , – частота вращения барабана в об/мин.
, – частота вращения барабана в об/мин.
При известном значении частота вращения барабана определяется по формуле;

Краевые значения G-фактора определяются из уравнения (12) ![]() ,при n=0, т.е. барабан не вращается. По графику рис.3 определяется минимальное значение G-фактора Kgб==0,7454
,при n=0, т.е. барабан не вращается. По графику рис.3 определяется минимальное значение G-фактора Kgб==0,7454
Формула (12) учитывает кинетическую энергию приобретаемую изделиями при отрыве от обечайки барабана.
Верхнее значение G-фактора определяется исходя из условий движения изделий в барабан, с учётом кинетической и потенциальной энергии выделяемой при ударе изделия об обечайку барабана.
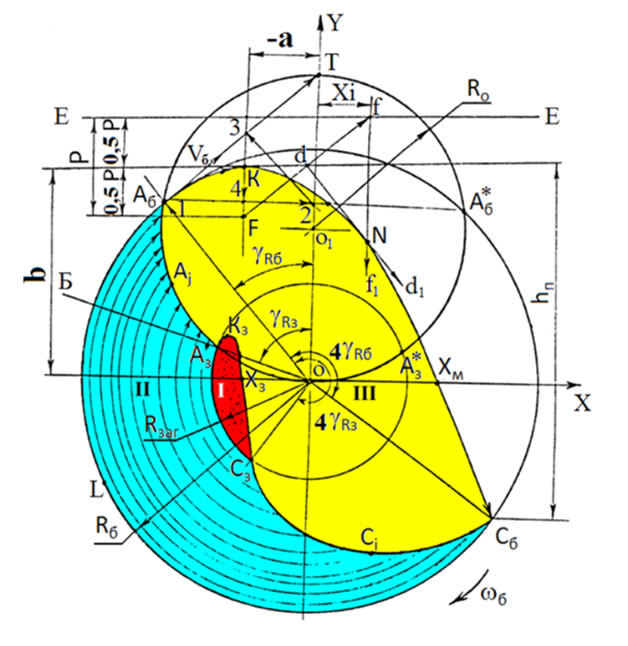
Рис 2. Графоаналитическое построение перемещения ткани изделий во вращающемся барабане СМ.
Rб – радиус барабана; ω б – угловая частота вращения барабана, рад/сек; Rо – радиус окружности отрыва; Rзаг – предельный радиус загрузки; γRб и γRз – углы отрыва по внешнему и внутреннему слою; Р – параметр параболы; F – фокус параболы; К – вершина параболы; hп – высота падения; Аб, Аi, Аз – линия отрыва; Сб, Ci, Cз – линия встречи; N – точка параболы, определяемая графическим построением; Xм – координаты пересечения параболы с осью ОХ; I – зона комкования; II – зона подъема; III – зона свободного полета.
Единичная масса единицы стираемого изделия из ткани (рис.2) после отрыва со своей орбиты радиуса достигает апогея, используя кинетическую энергию вертикальной составляющей скорости отрыва, и далее падает пол действием силы тяготения до встречи с обечайкой барабана. При ударе выделяется энергия, характеризующая гидромеханические свойства барабана стиральной машины и обуславливающая её основные показатели, в частности, показатель качества отстирываемости [3].
Кинетика процесса перемещения изделий из ткани представлена на рис.2, а математический аппарат, позволяющий определить траекторию перемещения изделий из ткани в барабане достаточно полно представлен в [1].
В точке отрыва единичная масса имеет следующий запас энергии, сообщаемый ей барабаном:
![]()
где ![]() , - потенциальная энергия единичной массы в точке отрыва;
, - потенциальная энергия единичной массы в точке отрыва; ![]() ,- кинетическая энергия единичной массы в точке отрыва.
,- кинетическая энергия единичной массы в точке отрыва.
Относительно оси ОХ:
![]()
![]()
Так как ![]() то
то
![]()
Из уравнений (13), (14), (15) следует:
![]()
представлены на рисунке 3.
В точки встречи в момент времени сразу после удара запас энергии определяется выражением:
![]()
![]()
![]()
![]()
Разность![]() и
и ![]() позволяет оценить гидромеханическое воздействие барабана стиральной машины на единичную массу с данной орбиты радиусом
позволяет оценить гидромеханическое воздействие барабана стиральной машины на единичную массу с данной орбиты радиусом![]() :
:
![]()
![]()
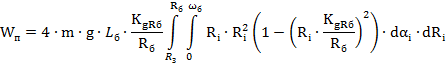 (19)
(19)
Подставим в уравнение (19) вместо ![]() её значение на формулы:
её значение на формулы:
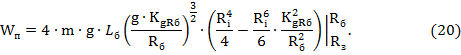
Приравняв нулю первую производную от (20) по ![]() и решив получившееся уравнение относительно коэффициента центробежного ускорения
и решив получившееся уравнение относительно коэффициента центробежного ускорения ![]() , можно найти оптимальное значение скорости вращения для заданного значения коэффициента загрузки
, можно найти оптимальное значение скорости вращения для заданного значения коэффициента загрузки ![]() .
.
В частности рассмотрим случай полной допустимой загрузки барабана при![]() :
:![]() то получим:
то получим:![]()
Решением уравнения (21) с точностью до 6 знай после запятой будет значение ![]()
Каждая орбита радиуса![]() имеет свои энергетические характеристики, определяемые уравнением (21). Максимум в уравнении достигается при
имеет свои энергетические характеристики, определяемые уравнением (21). Максимум в уравнении достигается при ![]()
![]()
После раскрытия скобок и упрощения получим:
![]()
![]()
![]()
![]()
что соответствует углу отрыва: ![]()
Максимальное значение запаса энергии, сообщаемой барабаном единичной массе ткани изделий достигается при условии:![]()
После преобразования получим:
![]()
![]()
Из (24) следует, что при любом значении коэффициента ![]() максимальное значение запаса энергии, сообщаемой барабаном единичной массе, достигается для той орбиты, точка отрыва которой соответствует значению
максимальное значение запаса энергии, сообщаемой барабаном единичной массе, достигается для той орбиты, точка отрыва которой соответствует значению ![]()
Из уравнения (25) следует, что при любом радиусе ![]() , максимальное значение запаса энергии, сообщаемой барабаном единичной массе ткани изделий, достигается при значении коэффициента центробежного ускорения, равного:
, максимальное значение запаса энергии, сообщаемой барабаном единичной массе ткани изделий, достигается при значении коэффициента центробежного ускорения, равного:
![]()
Оптимальное значение ![]() определяется такой частотой вращения барабана, при котором обеспечивается максимальное значение суммы высот падения изделий
определяется такой частотой вращения барабана, при котором обеспечивается максимальное значение суммы высот падения изделий![]() (рис 2) для всех слоев изделия с радиусом
(рис 2) для всех слоев изделия с радиусом ![]()
Введём понятие параметрического радиуса барабана, который определяется по формуле:
![]()
где ![]() текущий радиус по слоям изделий, которые прижимаются и поднимаются обечайкой барабана за счет центробежных сил.
текущий радиус по слоям изделий, которые прижимаются и поднимаются обечайкой барабана за счет центробежных сил.
Тогда, высота падений изделий ![]() (рис 3) определяется по формуле:
(рис 3) определяется по формуле:
![]() ,
, ![]() ,
,
где ![]() - параметрический радиус изменяется от 0 до 1, а
- параметрический радиус изменяется от 0 до 1, а ![]()
Расчётные значения ![]() при изменении параметрического радиуса
при изменении параметрического радиуса ![]() от 0 до 1 и значениях
от 0 до 1 и значениях![]() , от 0 до 1,. представлены на рис. 4
, от 0 до 1,. представлены на рис. 4
На основание расчетных данных строится зависимость Si от![]() (рис. 4). Для нахождения оптимального значения G-фактора использован классический [5] принцип максимума, сведенный до краевой задачи, где граничными уровнями является G-фактор. Решение задачи получено графоаналитическим путем описанный множеством данных с полиноминальным законом распределения и коэффициентом достоверности, состава соответствующим R-0.998. Получение значения максимума соответствует 0,7413 и f(Si) →max и f(Kgб)→0,7453, f(γ)→45° - оптимальный угол отрыва. Условия оптимальности являются достаточными и не требуют дополнительной проверки на оптимум
(рис. 4). Для нахождения оптимального значения G-фактора использован классический [5] принцип максимума, сведенный до краевой задачи, где граничными уровнями является G-фактор. Решение задачи получено графоаналитическим путем описанный множеством данных с полиноминальным законом распределения и коэффициентом достоверности, состава соответствующим R-0.998. Получение значения максимума соответствует 0,7413 и f(Si) →max и f(Kgб)→0,7453, f(γ)→45° - оптимальный угол отрыва. Условия оптимальности являются достаточными и не требуют дополнительной проверки на оптимум
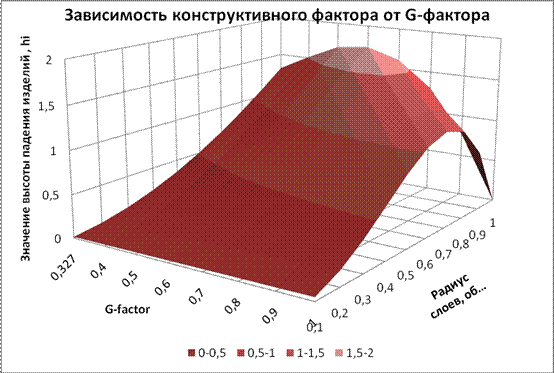
Рис 3 Оптимизация значения ![]()
На основание расчетных данных строится зависимость ![]() от
от ![]() при изменении значений
при изменении значений![]() от 0,327 до 1 (рис. 3).
от 0,327 до 1 (рис. 3).
Далее рассчитываются площади Si под кривыми ![]() (рис.4):
(рис.4):
![]()
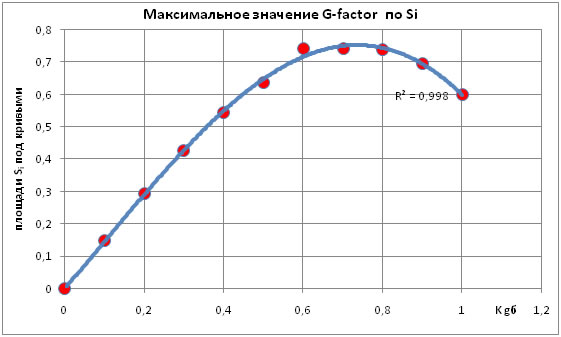
Рис 4 Определение максимального значение Sмах и ![]()
Заключение. Исследование существующих закономерностей кинетики перемещения изделий из ткани во вращающемся барабане СОМ [1] позволил авторам разработать математический аппарат моделирования процессов стирки. Такая модель достоверно описывает основные нагрузки на поток обрабатываемого в барабане материала, что позволило моделировать разные конструктивные параметры на выходе математической системы. Адекватность [3] полученной модели характеризуется значением основного параметра интенсификации механического фактора, путем решения задачи конечномерной оптимизации, обеспечивающие минимальное значение относительной погрешности моделирования.
В данной работе получено решение оптимизационной задачи, по определению максимальной высоты падения изделий из ткани в барабане в процессе стирки, с минимальной окрестностью данных искомой величины. В рамках решения этой задачи, согласно полученным зависимостям рассчитана величина оптимального G-фактора, соответствующей максимальной высоте паления. Решение такой задачи является основой ресурсосберегающего совершенствования процессов стирки, полоскания и отжима являются актуальными инструментами проектировщика профессионального прачечного оборудования.
Литература
1.Набережных А.И. Бытовые стиральные машины [Текст]*/ А.И. Набережных, Л.В. Сумзина : учебное пособие. – М.: МГУ Сервиса, 2000. – 176 с.
2.Лебедев, В. С. Технологические процессы машин и аппаратов в производствах бытового обслуживания [Текст]*/ В.С.Лебедев. – М.: Лёгпромбытиздат, 1991.– 335 с.
3.Набережных А.И., Куприянов А.В. Теория и практика создания современных стиральных машин для бытового обслуживания с безреверсивным процессом стирки [Текст]*/ А.И. Набережных, А.В. Куприянов/ Наука сервису: X-ая межд. научн.-практ. конф. 2Т. под ред. д-ра техн. наук проф. В.С. Шуплякова. – М. : ГОУВПО «МГУС», 2005. – 165с.
4.Набережных А.И., Куприянов А.В. Исследование влияния температурного фактора на качество стирки [Текст]*/ А.И. Набережных, А.В. Куприянов/ В мире научных открытий. Красноярск: НИЦ, – 2011. – №8.1 (20). – 196 с. – С. 357-369.