Оценка критерия обобщенной работы при оптимизации управления мехатронным объектом изменяемой структуры
Аннотация
В статье приводится математическая модель функционирования мехатронного объекта изменяемой структуры, описываемая предикатно-дифференциальными и предикатно-разностными уравнениями. Выведено выражение для оценки или изменяемой части дискретного аналога критерия обобщенной работы при оптимизации управления мехатрон-ным объектом изменяемой структуры.
Ключевые слова: мехатронный объект изменяемой структуры, оценка критерия обобщенной работы, прогнозирующая модель, оптимальный алгоритм управления с прогнозирующей моделью, предикатно-дифференциальные уравнения, предикатно-разностные уравнения.
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
В статье приводится математическая модель функционирования мехатронного объекта изменяемой структуры, описываемая предикатно-дифференциальными и предикатно-разностными уравнениями. Выведено выражение для оценки или изменяемой части дискретного аналога критерия обобщенной работы при оптимизации управления мехатронным объектом изменяемой структуры.
Ключевые слова: мехатронный объект изменяемой структуры, оценка критерия обобщенной работы, прогнозирующая модель, оптимальный алгоритм управления с прогнозирующей моделью, предикатно-дифференциальные уравнения, предикатно-разностные уравнения.
1. Математическая модель функционирования мехатронного объекта изменяемой структуры. В терминах обобщенных функций (производных) математическая модель функционирования объекта изменяемой структуры может быть представлена в виде:
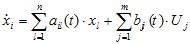(1.1)
или в матричной форме
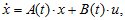(1.2)
где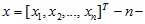 
мерный вектор-столбец состояния объекта управления; 
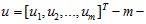мерный вектор-столбец управлений;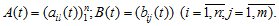 
Коэффициенты математической модели (1.1) объекта изменяемой структуры с течением времени имеют скачки, которые можно описать на понятии гибридной функции [1]. По определению, гибридная функция есть произведение некоторой числовой функции и функции предикат. Обозначим функцию предикат буквой L. Тогда описанием изменения коэффициента в (1.1) с учетом наличия скачков может служить выражение:
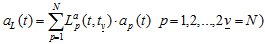(1.3)
с условиями единственности
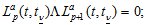(1.4)
и полноты
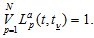(1.5)
Учитывая выражения (1.3)–(1.5), математическая модель функционирования объекта изменяемой структуры (1.1) может быть представлена в виде:
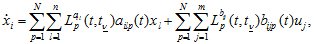(1.6)
с условиями единственности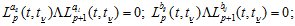 
и полноты
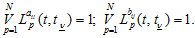
В матричном виде в соответствии с (1.2) она запишется в следующей форме:
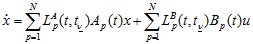(1.7)
с соответствующими условиями единственности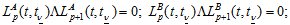 
и полноты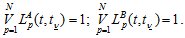 
Математическая модель функционирования объекта изменяемой структуры вида (1.6) или (1.7) описывается предикатно-дифференциальными уравнениями. Для построения дискретной модели воспользуемся приближенным методом первых разностей [2]. Тогда в соответствии с (1.7) запишем
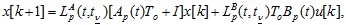(1.8)
Учитывая, что
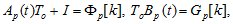
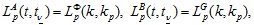
запишем (1.8) следующим образом:
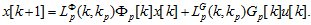(1.9)
Так как количество интервалов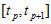 
равно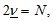 
то запишем сумму по всем 
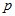в правой части (1.9)
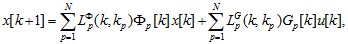(1.10)
с условиями единственности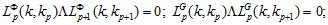 
и полноты
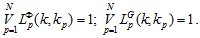
Уравнение (1.10) с соответствующими условиями единственности и полноты будет являться дискретной математической моделью мехатронного объекта. Эта модель представлена предикатно-разностными уравнениями.
2. Изменяемая часть дискретного аналога критерия обобщенной работы. В [3, 4] А.А. Красовским предложен так называемый критерий обобщенной работы. Им введен в минимизируемый функционал дополнительный член, являющийся оценкой сигналов управления в оптимальной системе. Укажем выражение для определения оценки или изменяемой части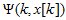 
дискретного аналога критерия обобщенной работы.
На основании результатов связи метода функций Ляпунова с методом динамического программирования [5] оптимальное управление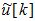 
минимизирует функционал
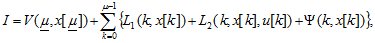(2.1)
если существует положительно определенная функция Ляпунова-Беллмана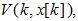 
удовлетворяющая условиям:
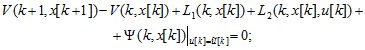(2.2)
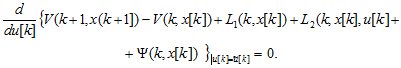(2.3)
Здесь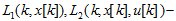 
положительно определенные функции, определяющие соответственно оценку координат объекта и оценку управлений с координатами объекта.
В соответствии с [6,7], разлагая функцию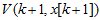 
в ряд Тейлора относительно вектора 
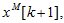определяемого моделью
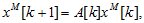
запишем выражение
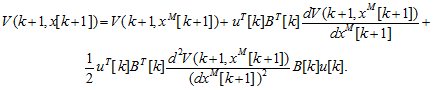(2.4)
Подставляя (2.4) при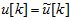 
в условие (2.2), получим
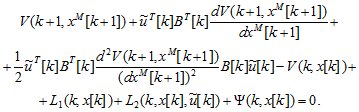(2.5)
Тогда учитывая, что положительно определенная функция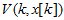 
при оптимизации управления по дискретному аналогу критерия обобщенной работы определяется уравнением
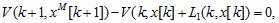
из (2.5) получим изменяемую часть дискретного аналога критерия обобщенной работы в виде
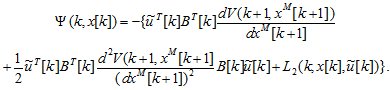(2.6)
ЛИТЕРАТУРА
1. Терно О.Р. Гибридные функции – новый метод описания сложных систем // Изв. АН СССР. Техническая кибернетика. 1965. № 6.
2. Кузовков Н.Т., Карабанов С.В., Салычев О.С. Непрерывные и дискретные системы управления и методы идентификации. – М.: Машиностроение, 1978.
3. Красовский А.А., Буков В.Н., Шендрик В.С. Универсальные алгоритмы оптимального управления непрерывными процессами. – М.: Наука, 1977.
4. Красовский А.А. Системы автоматического управления полетом и их аналитическое конструирование. – М.: Наука, 1973.
5. Смирнов Ю.А., Тищенко Л.Г. Синтез дискретного алгоритма управления положением исполнительных органов объекта, описываемого логико-разностными уравнениями // Изв. ВУЗов. Приборостроение. 1984. № 6.
6. Смирнов Ю.А. Синтез оптимальной программы настройки параметров прогнозирующей модели объекта изменяемой структуры. Математические методы и технологии в технике: Сб. науч. тр. / Саратовский гос. университет. Саратов, 2008.
7. Смирнов Ю.А. Адаптивная система управления. Авторское свидетельство СССР №1464139, кл. G 05 B 13/02, 1987.