К расчету оболочек вариационно-энергетическим методом
Аннотация
В данной статье получено выражение для потенциальной энергии деформации произвольной оболочки, численно равной работе внутренних сил, в криволинейной системе координат, совпадающей с линиями кривизны срединной поверхности оболочки, которое используется при расчете оболочек вариационно-энергетическим методом .
Ключевые слова: оболочка, вариационно-энергетический метод, минимума полной потенциальной энергии системы, перемещения, деформации.
Вариационно-энергетический метод расчета оболочек и других конструкций основан на принципе минимума полной потенциальной энергии системы, являющимся одним из основных принципов механики сплошной среды.
Полная потенциальная энергия системы (Э) равна разности работы внутренних и внешних сил
Э=А - Авн
За основные неизвестные принимаются компоненты перемещения произвольной точки срединной поверхности оболочки вдоль осей криволинейной системы координат в виде бесконечных двойных рядов
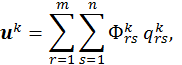
где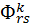 
− аппроксимирующие функции выбираются так, чтобы удовлетворялись геометрические граничные условия; 
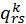− неизвестные постоянные коэффициенты, определяемые из условия минимума полной потенциальной энергии системы.
Согласно принципу минимума полной потенциальной энергии системы, действительному деформированному состоянию системы отвечает минимальное значение ее полной потенциальной энергии.
Функция полной потенциальной энергии системы (Э) после подстановки в нее компонент перемещения uk , будет являться квадратичной функцией многих независимых перемещений 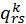. Необходимым условием экстремума этой функции является равенство нулю ее частных производных по переменным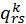
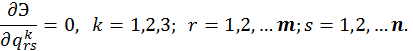
Полученная система представляет собой систему 3mn линейных уравнений относительно 3mn неизвестных коэффициентов 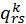. Полученные коэффициенты позволяют определить не только перемещения, но и деформации и напряжения в любой точке тонкостенной конструкции.
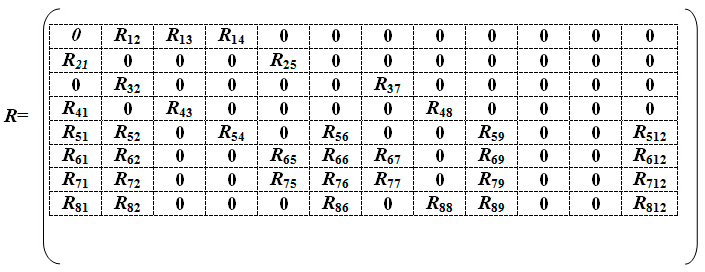
Для расчета оболочки любой формы, для которой найдены линии кривизны, получено выражение для работы внутренних сил (А) в матричном виде.
При получении этого выражения были приняты гипотезы Киргофа-Лява. Система координат криволинейная, ортогональная и совпадает с линиями кривизны срединной поверхности оболочки
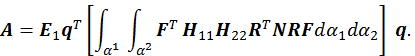
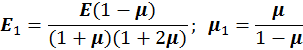
E−модуль упругости первого рода, − коэффициент Пуассона
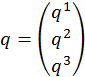
(3mn×1)
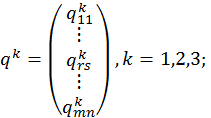
(mn×1)
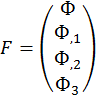
(12×3mn)
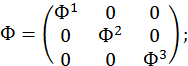
(3×3mn)
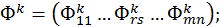
(1×mn)
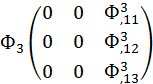
(12×3mn)
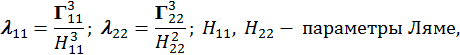
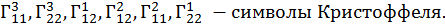
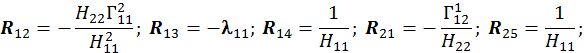
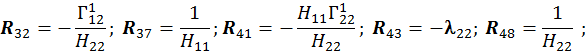
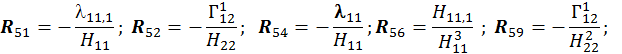
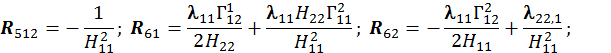
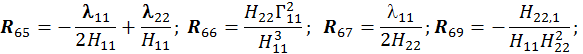
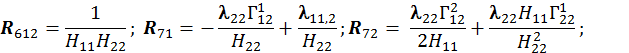
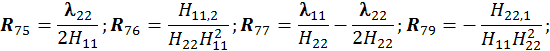
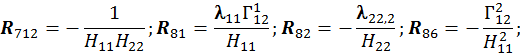
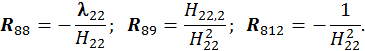
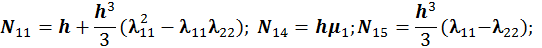
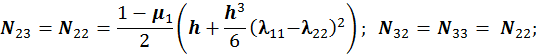
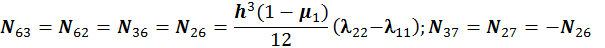
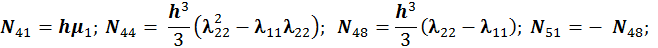
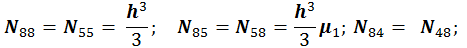
Литература
1.Аксентян К.Б., Гордеев-Гавриков В.К. Энергетический метод расчета оболочек усложненной формы. Издательство Ростовского университета, 1976г.
2. Гольденвейзер А.Л. Теория упругих тонких оболочек М. «Наука» ,1976г.
3.Филин А. В. Элементы теории оболочек Изд. второе, дополн. и перераб.- Л.: Стройиздат,
1975г.