Реология соляного массива со сферической полостью

Аннотация

Языев С.Б., Языев Б.М, Литвинов С.В.

Данная статья связана с технологической проблемой создания полостей с помощью камуфлетных взрывов, при которых температура внутри полости существенно превышает начальную температуру массива. Часто такие полости создаются в массиве каменной соли. Поскольку в каменной соли даже при небольших нагрузках проявляются явно выраженные реологические свойства, представляет интерес решение задачи о ползучести соляного массива с полостью при действии как силовых (давление внутри полости и давление грунта), так и температурных нагрузок.

Ключевые слова: неоднородность, ползучесть, высокоэластические деформации, соляной массив, уравнение связи, интегральные соотношения

05.23.17 - Строительная механика

Данная задача связана с технологической проблемой создания полостей с помощью камуфлетных взрывов, при которых температура внутри полости существенно превышает начальную температуру массива. Часто такие полости создаются в массиве каменной соли [1]. Поскольку в каменной соли даже при небольших нагрузках проявляются явно выраженные реологические свойства, представляет интерес решение задачи о ползучести соляного массива с полостью при действии как силовых (давление внутри полости и давление грунта), так и температурных нагрузок [2]. При этом возможен не только нагрев, но и охлаждение массива.

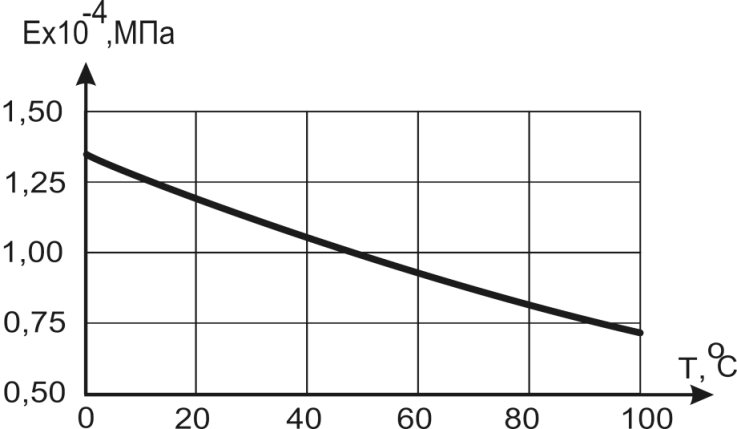
Рис. 1. ̶  Зависимость модуля упругости каменной соли от температур

Согласно рекомендациям [2] величину E следует определять в точке диаграммы,  соответствующей σ = 0,4R_пр,  где  R_пр – призменная прочность. На рис.1 приведены экспериментальные точки зависимости модуля упругости каменной соли от температуры, полученные в интервале 20ºC << T << 100ºC и аппроксимирующая кривая E(T).

Для описания процесса ползучести каменной соли при повышенных температурах можно использовать приведенную в [2] зависимость, имеющую при одноосном нагружении вид:

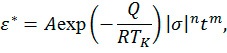(1)

где Q – энергия активации ползучести; R – газовая постоянная; T_K – температура; K; A, n и m – эмпирические коэффициенты. На основании проведенных экспериментальных исследований ползучести в интервале 20ºC << T << 100ºC в [4] получены следующие значения параметров соотношения (1):

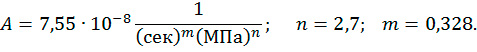
При сложном напряженном состоянии для скоростей деформаций ползучести с учетом (1) получим

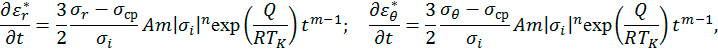(2)

где σ_i  – интенсивность напряжений.

Граничные и начальные условия задачи представляются в виде:

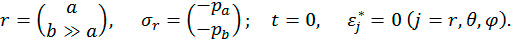
Здесь p_a – возможное внутреннее давление в полости, p_a = γH – давление отпора среды в предположении H>>b.

Ниже приводятся результаты расчета, полученные методом «послойного» интегрирования с переменным шагом по времени и радиусу при следующих исходных данных: a = 2 м; b = 10 м; p_b = 21,5 Мпа; v = 0,275; T_a = 100ºC; T_b = 100ºC.

На рис. 2 показаны эпюры напряжений σ_θ для различных моментов времени. Следует отметить, что в процессе ползучести напряжения вблизи контура полости существенно снижаются, а по мере удаления от полости возрастают, что связано с необходимостью выполнения интегрального уравнения равновесия

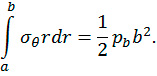(3)

Последняя формула может быть получена из рассмотрения элемента массива со сферической полостью (рис. 4). Составим проекцию всех сил, действующих на данный элемент, на ось 0_z. Интеграл от напряжений σ_θ

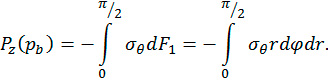(4)

Проекцию на ось z интегрального усилия от давления p_b можно определить по формуле

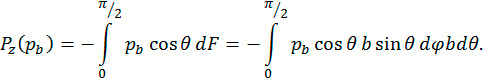(5)

Вычисляя последний интеграл, суммируя выражения (4) и (5) и сокращая все на dφ, приходим к равенству (3). При этом следует обратить внимание на то, что заметный рост напряжений σ_θ в процессе ползучести вблизи внешнего контура вырезанного массива (см. рис. 2)  обусловлен рассмотрением приближенной модели, т.е. конечным значением b (в расчете принималось b = 5a). В действительности же при b → ∞ влияние отверстия и неоднородности не должно сказываться на значениях напряжений на большом расстоянии от отверстия.

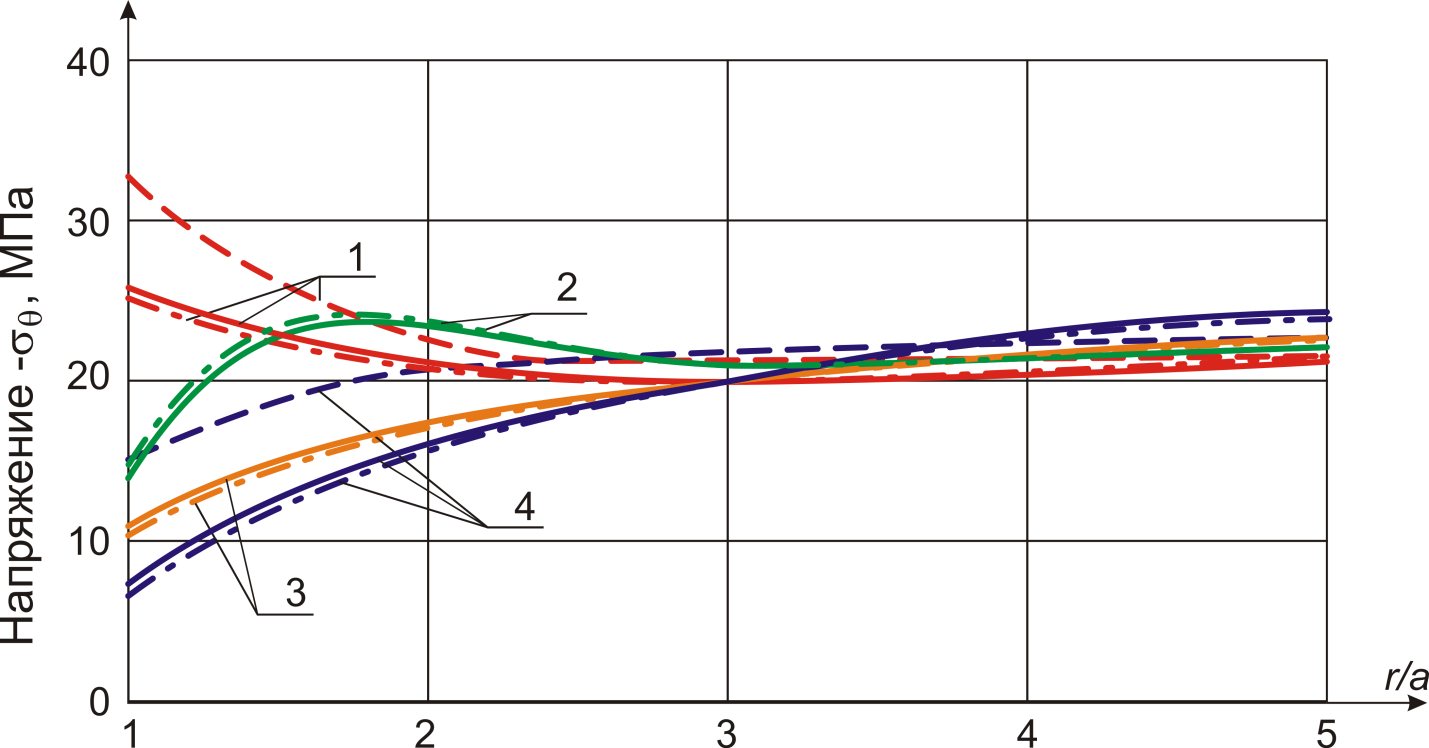
Рис. 2. Перераспределение во времени напряжений σ_θ в массиве со сферической полостью:
однородный массив (T = 20ºC);
неоднородный массив (T_a = 100ºC, T_∞ = 20ºC);
неоднородный массив (T_a = 100ºC, T_∞ = 20ºC), решение, приводимое в [10];
1 - t = 0 (упругое решение); 2 - t = 18 ч; 3 - t = 52 ч; 4 - t = 21000 ч.

На рис. 3 приведены эпюры перемещений в массиве с полостью для некоторых моментов времени. При этом фактические перемещения следует отсчитывать от прямой (показана штрих-пунктиром), соответствующей сжатию упругого массива без полости.

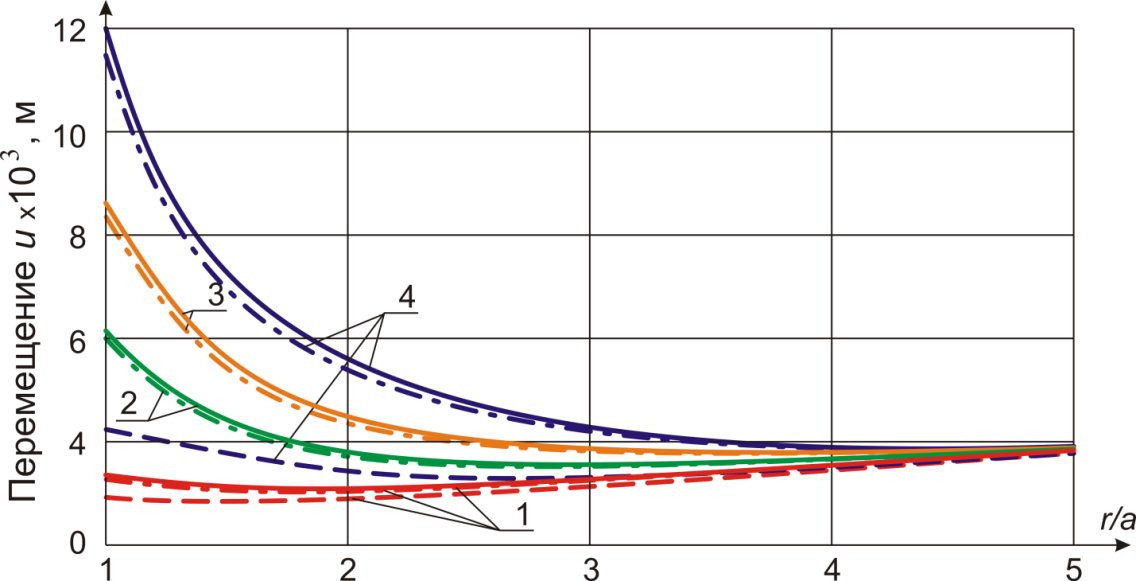
Рис. 3. Перемещения в массиве со сферической полостью:
однородный массив (T = 20ºC);
неоднородный массив (T_a = 100ºC, T_∞ = 20ºC);
неоднородный массив (T_a = 100ºC, T_∞ = 20ºC), решение, приводимое в [10];
1 - t = 0 (упругое решение); 2 - t = 18 ч; 3 - t = 52 ч; 4 - t = 21000 ч.

При ползучести так же, как и в теории пластичности, принимается гипотеза о несжимаемости материала, в связи, с чем дальнейшее сокращение объема сплошного массива по сравнению со стадией упругой работы не происходит.   

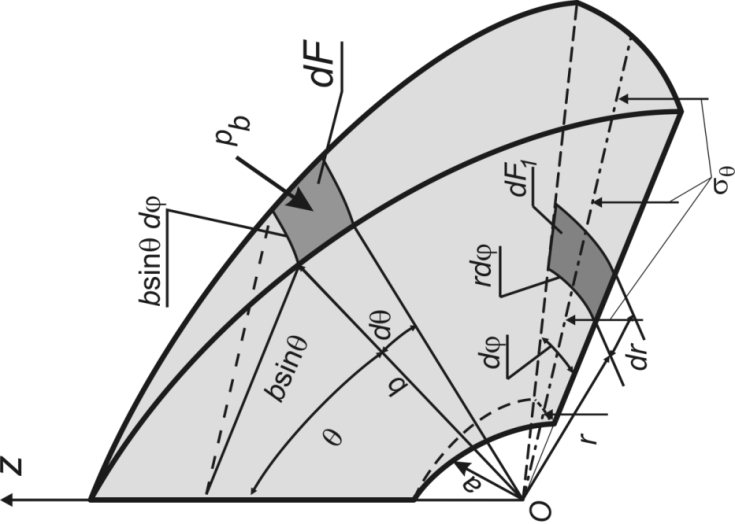
Рис. 4.  ̶  Схема проверки равновесия массива со сферической полость

Литература

1. Мясников К.В., Леонов Е.А., Ромадин Н.М. Разработка научно-технических основ создания подземных хранилищ с помощью ядерных взрывов в массиве каменной соли // Сб. Peaceful Nuclear Explosions, III, 1974, Vienna, p. 179-191.

2. Андреев В.И. Упругость и ползучесть неоднородной полой сферы / Андреев В.И. [и др.] // Всес. Конф. «Фундам. исслед. и новые технологии в строительном материаловедении»: тез. докл. – Белгород, 1989. – С.6.

3. Языев Б.М. Нелинейная ползучесть непрерывно неоднородных цилиндров: дис. … канд. техн. наук. – М., 1990. – С. 171.

4. Туребаева Р.Д. Ползучесть неоднородного массива с цилиндрической полостью: дис. … канд. техн. наук. – М., 1994. – 117 с.