Регулировочные характеристики планетарного генератора момента

Аннотация

С.А. Кузнецов, В.А. Лысянский

В статье исследованы зависимости сопротивления на водиле планетарного механизма от управляющего момента на центральном колесе. Предложена в соответсвии с методом электромеханических аналогий гипотеза о активной и реактивной составляющих механического сопротивления. Представлены результаты экспериментальных исследований регулировочной характеристики генератора момента подтверждающие теоретические положения. 

Ключевые слова: генератор момента, регулировочная характеристика, электромеханические аналогии, реактивное сопротивление

05.02.02 - Машиноведение, системы приводов и детали машин

Кинематическая схема стенда для испытания зубчатых колес и смазок представлена на рис. 1. Числа зубьев колес 2 и , 1 и 3 попарно равны между собой, причем к колесу 1 жестко прикреплен рычаг 5, воздействуя на который можно управлять моментом на водиле механизма [1].
Принцип работы заключается в следующем. Вращение подается на входное звено (водило) 4, которое вместе с сателлитным блоком, образованным колесами 2 и , свободно вращается вокруг центральных колес 3 и 1, которые остаются неподвижными, поскольку колесо 3 закреплено неподвижно.

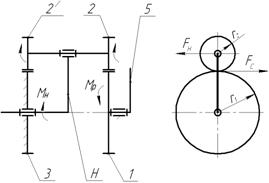
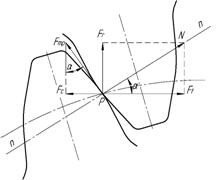
Рис. 1. – Кинематическая схема нагружателя и схема сил, действующих в зубчатом зацеплении
1 – подвижное центральное колесо; 2 и  – сателлиты; 3 – неподвижное центральное колесо; 4 – водило (Н); 5 – рычаг управления

При приложении управляющего момента на рычаг 5 свободное движение водила Н с блоком сателлитов затормаживается, и на валу водила Н возникает момент сопротивления, причем этот момент пропорционален управляющему усилию. Кинематическое передаточное отношение, определенное по известной формуле, равно нулю (от первого колеса к водилу), либо бесконечности (от водила к первому колесу), поэтому передача движения в любом случае невозможна. Невозможно в свете современных представлений говорить в таком случае и о силовом передаточном отношении, поскольку оно определяется через кинематическое.
Тем не менее, поскольку воздействие на рычаг управления 5 изменяет момент сопротивления на валу водила, можно использовать данное устройство в качестве генератора момента вместо тормоза или нагрузочного устройства и регулировать нагрузкой на рычаге создаваемый на водиле момент. Установлено, что, в отличие от фрикционного тормоза, на планетарном нагружателе при сравнимой нагрузке тепловая энергия выделяется в малом количестве, сравнимом с выделением тепла в простой зубчатой передаче. Объяснить это можно наличием как активного, так и реактивного сопротивления при работе генератора момента. В соответствии с известным методом электромеханических аналогий [2, 3], полное механическое сопротивление по аналогии с полным электрическим сопротивлением (табл. 1) включает в себя как активную составляющую (), так и реактивную (), причем реактивное сопротивление определяется емкостным () и индуктивным ()сопротивлением цепи (применительно к механической системе это гибкость () звеньев и их масса ()).

Таблица 1
Электромеханические аналогии

Полное электрическое сопротивление определяется
.
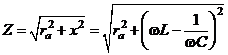Подобно реактивному сопротивлению электрической цепи , являющейся разностью индуктивного и емкостного сопротивлений, реактивное сопротивление механической системы  является разностью инерционного  и упругого сопротивлений , и полное механическое сопротивление в соответствии с методом электромеханических аналогий определяется
.
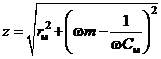В механизмах без самоторможения реактивная составляющая обычно очень мала, поэтому в большинстве случаев не учитывается. В случае самотормозящего механизма механическое сопротивление возрастает пропорционально замыкающей силе (или моменту) на звене управления.

Активная часть механического сопротивления (трение)
Момент на водиле:

Сила , приложенная к водилу со стороны сателлита, уравновешивается силой , приложенной в полюсе зацепления первого колеса и сателлита, которая создает уравновешивающий момент,  также равный :
.
Сила  является составляющей силы трения , перпендикулярной оси водила (рис.1):
.
Соответственно, сила сопротивления с учетом силы трения:
.
Окружная сила выражается через момент управляющий , приложенный     к звену 1:
.
С учетом этого сила сопротивления:
.
Момент на водиле , выраженный через управляющий момент :
.
Поскольку речь идет о генераторе момента, отношение моментов назовем  регулировочной характеристикой:
     (1)
Очевидно, что активная составляющая механического сопротивления, связывающая моменты на звене управления 1 и водиле Н, зависит только от угла зацепления и коэффициента трения между зубьями и не зависит от числа зубьев и кинематического передаточного отношения. Активная часть регулировочной характеристики меньше единицы, причем намного: при  и коэффициенте трения  она равно всего лишь 0,036, что примерно соответствует значению активной составляющей на экспериментальном графике (рис. 5а).

Реактивная составляющая механического сопротивления
Для существования реактивного сопротивления необходимы три условия: наличие колебаний момента на ведомом колесе; наличие упругих свойств материалов зубчатых колес и наличие у них инертности, то есть масс или моментов инерции. Если наличие последних двух условий не вызывают сомнения в отношении любой зубчатой передачи, то наличие крутильных колебаний в процессе взаимодействия каждой пары зубьев при постоянном  кинематическом передаточном отношении требует пояснений. Тем не менее ряд исследователей (С.Н. Кожевников [4], В.А. Гавриленко со ссылкой на Л.Н. Решетова [5]) по-разному, но с аналогичным результатом обосновывают флуктуации точки пересечения линии действия силы в зацеплении с линией центров, обусловленные действием силы трения в зацеплении. В процессе зацепления эта точка изменяет свое положение, то приближаясь к полюсу Р, то удаляясь от него. Но все время она находится с одной стороны от полюса Р, а именно со стороны ведомого колеса (рис. 2). Гавриленко [6] приводит формулы для определения положения точки D в текущий момент времени, а также максимальные значения ее удаления и среднее, причем приводит в конечном итоге приближенное значение расстояние h от полюса до точки D:
 ,
где    m – модуль зацепления;
f – коэффициент трения между зубьями.
В.А. Гавриленко приводит также диаграмму изменения момента и силы взаимодействия зубьев, из которой видно, что возникающие в процессе взаимодействия зубьев колебания имеют характер, далекий от гармонических (рис. 2). В любом случае, данные колебания вполне могут вызывать инерционные потери, обусловленные реактивными сопротивлениями.

   
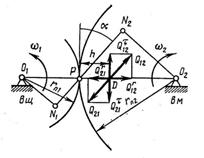
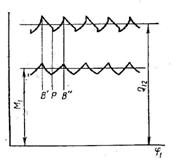
Рис. 2. Определение расстояния h  и циклические флуктуации момента и силы (по В.А. Гавриленко)

Полученная экспериментально зависимость (рис. 6) регулировочной характеристики  от момента управляющего  (характеристика сопротивления) имеет нелинейный вид обратно пропорциональной зависимости, которую можно представить в виде гиперболической функции:
,   (2)
где    а – постоянная величина, характеризующая кривизну гиперболы;
 – активная часть функции (мало изменяемая), связанная с влиянием момента холостого хода , то есть обусловленная активной частью сопротивления.
Задача формализации зависимости характеристики сопротивления сводится в данном контексте к отысканию значений постоянной а, приближенно соответствующей кривизне каждой из кривых семейства на рисунке 6.
Для этого выразим а из (2):
.
После подсчета значений а по данным каждой из кривых определяется среднее арифметическое аср и его значение присваивается постоянной в уравнении (2) каждой кривой (рис. 6а). Так, при вращения водила с частотой мин значение постоянной а = 0,018; при вращения водила с частотой  мин, значение постоянной а = 0,03; при вращения водила с частотой  мин значение постоянной а = 0,044. Эти значения соответствуют  экспериментальным значениям начальной ординаты на графике регулировочной характеристики, то есть постоянной линейного графика (рис.4). При этом тангенс угла наклона регулировочной характеристики равен активной части механического сопротивления
С целью определения регулировочной характеристики планетарного нагружателя, которое представляет собой соотношение движущего момента  на двигателе и момента управляющего , приложенного к рычагу нагружателя, был изготовлен стенд (рис. 3), содержащий двигатель постоянного тока 7, который посредством муфты 6 соединен с испытуемым нагружателем, блок питания 10, а также контрольно-измерительные приборы для регистрации напряжения 8 и силы тока 9 [7].
При включении питания ротор электродвигателя 7 через муфту 6 вращает вал водила 4 нагружателя. Приложение силы тяжести от груза к рычагу нагружателя 5 вызывает изменение момента на валу электродвигателя, который регистрируется амперметром 9.
Точность измерений обеспечена использованием стандартного измерительного прибора – мультиметра АРРА 305 с погрешностью измерения силы тока 0,2%, напряжения 0,06% на любом участке измерения при температуре 20°С.

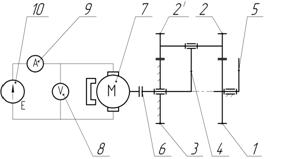
Рис. 3. Принципиальная схема стенда для определения регулировочной характеристики нагружателя- 1 – подвижное центральное колесо; 2, 2´ – сателлиты; 3 – неподвижное центральное колесо; 4 – водило; 5 – рычаг управления 6 – муфта; 7 – электродвигатель; 8 – вольтметр;
9 – амперметр; 10 – источник питания

В стенде используется электродвигатель постоянного тока CM31D17NZ8C с возбуждением от постоянных магнитов фирмы LEESON.
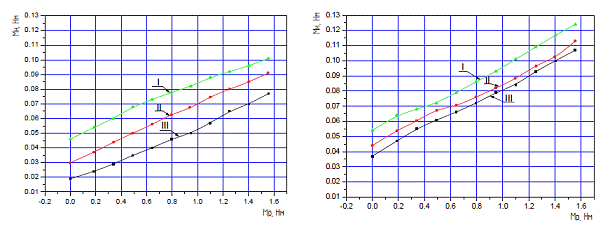
В результате экспериментальных исследований было установлено, что зависимость момента на водиле Мд  от момента на управляющем колесе 1 нагружателя, то есть регулировочная характеристика, имеет близкий к линейному вид, причем изменение направления вращения (или знака момента управляющего) не изменяет эту характеристику (рис. 4). Очевидно, что она зависит от частоты вращения n водила, но угол наклона остается постоянным.

      а                                                            б  
Рис.4. Регулировочная характеристика
а) металлические шестерни; б) пластмассовые шестерни
I) - при  мин, II) - при  мин, III) - при  мин

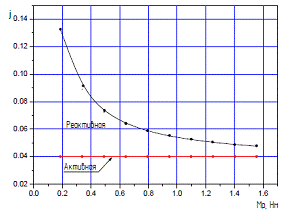
Характеристика сопротивления, создаваемого генератором момента, представляет вид, обратный регулировочной (рис 5,а). Активную составляющую характеристики сопротивления   определяем с учетом предварительно измеренного момента холостого хода ,
,
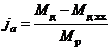При этом она остается примерно постоянной и равной  (рис. 5а).
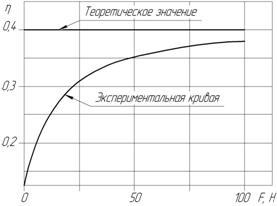
Приведенный для сравнения график изменения коэффициента полезного действия для механизма с самоторможением (например, винтового рис. 5,б) демонстрирует сущность инвертного подхода, состоящая в  обращеннности характеристики сопротивления по отношению к графику КПД: на этом графике также есть постоянная часть, соответствующая теоретическому КПД, и гиперболически возрастающая переменная часть, полученная также с учетом момента холостого хода.

Рис. 5. Графики зависимости: а) характеристика сопротивления; б) КПД винтового механизма

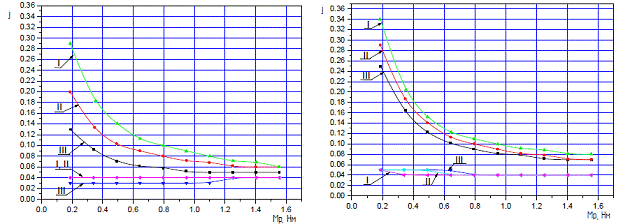
Для проверки влияния коэффициента трения на характеристику сопротивления были проведены экспериментальные исследования с различными смазочными материалами. Эксперимент показал, что основная, то есть реактивная часть характеристики сопротивления мало зависит от применяемой смазки, поскольку в рабочем диапазоне их коэффициент трения отличается незначительно.

а)                                                                б)
Рис. 6. Характеристики сопротивления:
а) металлические шестерни; б) пластмассовые шестерни
I) - при  мин, II) - при  мин, III) - при  мин

Гораздо более существенное влияние на регулировочную характеристику оказывают скорости вращения водила и материалы зубчатых колес, что в целом подтверждает гипотезу о реактивном характере сопротивления (рис. 6). С увеличением частоты вращения возрастает момент холостого хода  (за счет реактивного сопротивления), то есть постоянная  кривизны гиперболы характеристики сопротивления. При замене стальных шестерен пластмассовыми, несмотря на снижение массы (момента инерции) зубчатых колес реактивное сопротивление растет за счет повышения жесткости материалов.

Литература

1. Пат. №2214585 Российская федерация C1 7 G 01 M 13/02. Стенд для испытания зубчатых колес [Текст] / Кузнецов С.Н., Косов А.В.; заявитель и правообладатель Южно-Российский государственный университет экономики и сервиса - № 2002103652/11; заявл. 08.02.2002; опубл. 20.10.2003, Бюл. № 29.
2. Римский-Корсаков А.В. Электроакустика [Текст] / А.В. Римский-Корсаков. М.: «Связь», 1973. – 272 с.
3. Фурдуев В.В. Электроакустика [Текст] / В.В. Фурдуев М.-Л.: Гостехиздат, 1948. – 515 с.
4. Кожевников С.Н. Теория механизмов и машин: [Текст] / Учеб.пособие для вузов. – М.: Машиностроение, 1969. – 584 с.
5. Решетов Л.Н. Расчет планетарных механизмов [Текст] / Л.Н. Решетов. М.: Машгиз, 1952.
6. Теория механизмов. Под ред. В.А. Гавриленко. [Текст] / Учеб.пособие для втузов. М.: «Высшая школа», 1973. – 511 с.
7. Лысянский В.А. Экспериментальное определение силового передаточного отношения планетарного нагружателя [Текст] / В.А. Лысянский, С. А. Кузнецов // Научный потенциал молодёжи – будущему России: межрегион. науч.- практ. конференция, 20 апреля 2012 г. / редкол.: П.Д. Кравченко [и др.] ВИС ФГБОУ ВПО «ЮРГУЭС» - Шахты: ФГБОУ ВПО «ЮРГУЭС», 2012. – С 64-66.