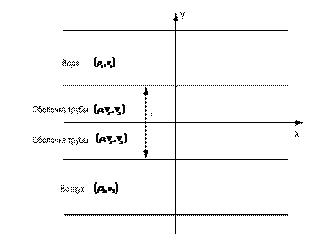Распространение акустической волны в замкнутой структуре водопровода на границе раздела сред
Аннотация
В работе рассмотрен случай, когда цилиндрическая труба не полностью заполнена водой, акустический излучатель расположен на оболочке водопроводной трубы. Показано, что для данного случая, целесообразно рассмотреть симметричные и ассиметричные режимы распространения акустической волны.
Ключевые слова: акустика, излучатель, волна, водопровод.
В последнее время в жилищно-коммунальном хозяйстве были предприняты значительные усилия для модернизации систем водоснабжения. Надежность, пригодность, безопасность и эффективность были идентифицированы как основные параметры, описывающие работу системы водоснабжения. Надежность - вероятность, что система будет работать правильно; пригодность - вероятность, что система будет эксплуатационной; безопасность - отсутствие опасных последствий для пользователей и окружающей среды и эффективность связана с уровнем потерь. При этом возникающие экологические проблемы и требования потребителей водных ресурсов, стали существенно влиять на развитие системы водоснабжения и соответственно улучшение услуг жилищно-коммунального хозяйства. Требования потребителей основаны на стремительном развитии передовых технологий систем водоснабжения, контрольно-измерительной аппаратуры и инфокоммуникационных технологиях.
Поэтому обрели свою актуальность разработки и технологии исследования магистральных водопроводных сетей, ультразвуковыми методами с целью повышения эффективности диагностики водопроводов, а также предупреждения чрезвычайных ситуаций и мониторинга экологической обстановки. При этом под технологией понимают совокупность аппаратно-программных комплексов, а также научно обоснованных методик их формирования и использования для исследований, включающих регистрацию конфигураций и размеров форм труб, а также фактов и тенденций их изменения.
В работах [1,2,3] авторами рассмотрены распространение акустической волны, распространяющейся внутри водопроводной трубы, полностью заполненной водой. Но существуют и другие режимы водного потока внутри водопроводной трубы (полностью и не полностью заполненная водой труба; с пузырьками воздуха и воздушными пробками и т.п.), которые существенно влияют на волновые процессы внутри трубы.
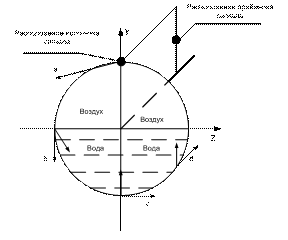
Рассматриваемый случай, когда жесткая цилиндрическая труба не полностью заполнена водой, акустический излучатель находится на оболочке трубы, является достаточно сложным с точки зрения распространения волн на границе раздела сред в замкнутой структуре рис. 1. Данный случай подразумевает решение ряда задач, а именно: распространение волны на границах раздела сред труба-воздух, воздух-вода и труба-вода (поскольку неизвестно какие режимы распространения волн возникают на границе труба-вода, предполагаем, что это низкий порядок мод направленной нормальной волны (похожей на волну Лэмба) и продольный/изгибный режимы распространения волн).
 |
|
Рис. 1 – Вид трубы не полностью заполненной водой
Оболочка цилиндрической трубы окружена с одной стороны водой, а с другой стороны воздухом. Обозначим плотность ![]() и звуковую скорость
и звуковую скорость ![]() в воде и воздухе
в воде и воздухе ![]() и
и ![]() соответственно; плотность, продольную и поперечную скорость в оболочке трубы
соответственно; плотность, продольную и поперечную скорость в оболочке трубы ![]() . В рассматриваемом случае считаем, что существует непрерывность давления и смещения частиц к поверхностям оболочки трубы
. В рассматриваемом случае считаем, что существует непрерывность давления и смещения частиц к поверхностям оболочки трубы ![]() . Уравнение для гармонической волны распространяющейся в направлении оси
. Уравнение для гармонической волны распространяющейся в направлении оси ![]() в произвольной гомогенной и изотропной среде имеет вид [4]:
в произвольной гомогенной и изотропной среде имеет вид [4]:
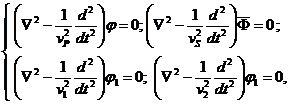
![]() ,
, ![]() ,
, ![]() .
.
где ![]() и
и ![]() – пространственно-временной скаляр и вектор потенциала, характеризующие смещение частиц
– пространственно-временной скаляр и вектор потенциала, характеризующие смещение частиц ![]() в оболочке трубы;
в оболочке трубы; ![]() и
и ![]() – скалярные потенциалы оболочки воды и воздуха.
– скалярные потенциалы оболочки воды и воздуха.
Для рассматриваемого случая принимаем во внимание только те решения, которые являются инвариантными ![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
,
где ![]() ;
; ![]() ;
; ![]() – неизвестные постоянные коэффициенты [5];
– неизвестные постоянные коэффициенты [5]; 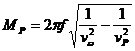 ;
; 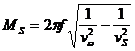 ;
; 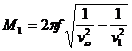 ;
; 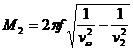 .
.
Для определения коэффициентов ![]() , зададим граничные условия:
, зададим граничные условия:
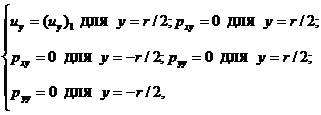
где 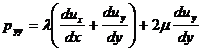 ;
; 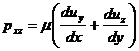 ;
; ![]() – коэффициенты [4].
– коэффициенты [4].
Проведя замены в уравнении для акустического давления, когда источник акустического сигнала расположен внутри упругой цилиндрической трубы [1,2,3], получаем решения для неизвестных коэффициентов ![]() :
:
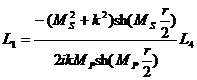 ;
; 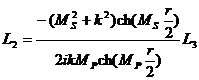 ;
;
![]() .
.
Симметричные моды: ![]() ;
; ![]() .
.
Асимметричные моды: ![]() ;
; ![]() .
.
Полученные коэффициенты позволяют определить акустическое давление в точке приёма для случая, когда водопроводная труба не полностью заполнена водой. При этом коэффициенты ![]() и
и ![]() , являются амплитудами асимметричной и симметричной моды акустической волны, значения коэффициентов
, являются амплитудами асимметричной и симметричной моды акустической волны, значения коэффициентов ![]() и
и ![]() , определяет прямое и противоположное смещение частиц в симметричном режиме распространения акустической волны. Коэффициенты
, определяет прямое и противоположное смещение частиц в симметричном режиме распространения акустической волны. Коэффициенты ![]() и
и ![]() определяют прямое и противоположное смещение частиц в асимметричном режиме распространения акустической волны.
определяют прямое и противоположное смещение частиц в асимметричном режиме распространения акустической волны.
Таким образом, можно сделать следующий вывод: отражения акустической волны на границе раздела нескольких сред будет значительно уменьшать энергию акустического давления и увеличивать многолучевое распространение.
Литература
1. Зибров, В.А., Сапронов, А.А. Использование пьезоэлектрических преобразователей для передачи информации о потребляемых водных ресурсах [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2009 - №3. - С. 78-81.
2. Зибров, В.А., Сапронов, А.А., Воробьев, С.В. Применение пьезоэлектрических преобразователей в системе дистанционного мониторинга потребляемых водных ресурсов в сфере жилищно-коммунального хозяйства [Текст// Электротехнические и информационные комплексы и системы. Научно-технический и теоретический журнал, 2010 - №1 - С. 17-23.
3. Сапронов, А.А., Зибров, В.А., Занина, И.А., Соколовская, О.В.. Исследование процесса передачи информации по акустическому каналу в водопроводе [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2012. – №4. – С.52-54.
4. Бреховских, Л.М., Годин, О.А. Акустика слоистых сред [Текст]: Монография.– М.: Наука. Главная редакция физико-математической литературы, 1989. – 416с.
5. Talrnant, M., «Rétrodiffusion d'une impulsion ultrasonore brève par une coque cylindrique à paroi mince», Ph.D. thesis, University of Paris VII, 1987