Использование пьезоэлектрических датчиков в системе мониторинга магистральных водопроводных сетей
Аннотация
При организации системы мониторинга магистральных водопроводных сетей, важной задачей является определение устойчивой работы передатчика и приемника акустической волны, выполненных на основе пьезоэлектриков.
Ключевые слова: акустика, контроль, пьезодатчик, водопровод.
Одними из главных и жизненно необходимых критериев комфорта современного жилого дома или учреждения являются отопление, водоснабжение и системы внутренних инженерных сетей. В соответствии с критериями можно поставить актуальные вопросы экологии и экономии, особенно экономии оплаты тех услуг, которыми люди пользуются не в полной мере, но платят исправно и в полном объеме. В настоящее время деятельность жилищно-коммунального хозяйства сопровождается весьма большими потерями ресурсов, как потребляемых самими коммунальными предприятиями, так и предоставляемых потребителям воды, тепловой и электрической энергии.
В то же время предприятия не имеют ни ощутимых стимулов, ни финансовых возможностей для замены в необходимых объемах устаревшего оборудования и изношенных основных фондов. Поэтому главную задачу участников процесса водоснабжения можно сформулировать, как комплексное использование всех рычагов управления спросом на ресурсы и стимулирования ресурсосбережения: техническое, экономическое, нормативное, институционное и информационное.
Решение этой задачи связано с осуществлением комплекса инженерно-технических мероприятий таких как: оптимизация режимов работы сетей водоснабжения через внедрение систем автоматизированного управления; применение аппаратуры контроля и диагностики состояния систем водоснабжения; новейших методов и технологий контроля и учета потребления водных ресурсов; проведение ремонтных работ в сетях водоснабжения зданий.
Применение ультразвуковой технологии передачи данных для учета энергоресурсов, позволит проводить мониторинг любых сред: жидкостей, газов, пара и т.п. Измерение и передачу данных можно проводить, применяя акустический ультразвуковой канал связи в магистрали продуктопровода при транспортировке тех или иных сред. Поэтому одним из важных моментов при организации надежного акустического ультразвукового канала связи, является определение устойчивой работы приемника и передатчика акустической волны, выполненных на основе пьезоэлектрических датчиков (ПД).
С целью обеспечения устойчивой работы ультразвуковых устройств в водопроводных сетях, необходимым является разработка и исследование схемы управления ПД. В работах [1,2] рассмотрены методики расчета программного управления линейными и нелинейными упругими механическими системами с конечным числом степеней свободы, описываемыми при помощи метода конечных элементов. Однако более надежными по отношению к помехам являются системы управления с обратной связью [3].
Рассмотрим методику синтеза управления системы с обратной связью на основе решения обратных задач динамики применительно к ПД.
Дифференциальное уравнение в матричной форме для линейной механической системы имеет следующий вид: 
, где 
, 
, 
– структурные матрицы жесткости, масс и демпфирования конечноэлементной модели; 
– электромеханическая матрица ПД; 
– вектор механических колебаний; 
– вектор управляющих воздействий. Рассмотрим случай апериодического колебания ПД: 
, где 
– вектор, определяющий конечное положение системы управления; 
<0, 
<0 – показатели экспонент.
Результаты измерения системы управления в разные моменты времени представим при помощи вектора: 
, где 
– матрица преобразования. Применяя аппарат псевдоподобных матриц запишем: 
, где 
– псевдоподобная матрица; 
– единичная матрица; 
– произвольный вектор; 
– неизвестная матрица постоянных величин.
Тогда 
. С учетом вышеизложенного материала, для линейной механической системы, уравнение примет следующий вид: 
. Будем считать, что измерению доступны 
и 
, тогда выразим ускорение через скорость и перемещение:
, (2)
. (3)
Тогда:
. (3)
Выразим значения возбуждающих усилий системы 
, где 
, 
– неизвестная матрица постоянных величин.
Входные усилия на ПД выразим в виде: 
. Результирующее уравнение системы с обратной связью для статического условия равновесия в момент времени 
примет вид:
. (4)
В момент времени 
, предположим 
, тогда для определения 
воспользуемся уравнением: 
, тогда наименьший по модулю вектор входных воздействий определим как 
. В выражение передаточных функций синтезированной системы управления пьезоэлектрическим преобразователем вводим произвольно заданные матрицы 
и 
. Для определения устойчивости системы воспользуемся первым методом Ляпунова, для чего запишем уравнение 
относительно 
-мерной матрицы столбца фазовых переменных 
в виде:
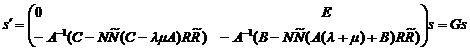. (5)
Для того чтобы полученная система была асимптотически устойчива, необходимо и достаточно, чтобы реальные части собственных значений матрицы 
были бы отрицательны. Представим матрицу 
как функцию от компонент матриц 
и 
в виде 
. Рассмотрим зависимость 
. Задача о собственных значениях для матрицы 
имеет вид: 
, где 
, 
– скаляры, действительная и мнимая части собственного значения; 
, 
– действительная и мнимая части собственного вектора.
Задача имеет 
решений 
, 
, 
, 
, 
. Рассмотрим все действительные части собственных значений
, среди которых в случае устойчивой системы все должны быть отрицательны. В случае наличия собственного значения с положительной действительной частью 
>0, следует изменить параметры 
, так чтобы она стала отрицательной. В силу нелинейной зависимости 
от 
для определения требуемых значений 
применим пошаговую процедуру, при этом текущие изменения 
будем определять пропорционально частным производным 
. Частные производные определим из следующего соотношения: 
, где 
и 
действительная и мнимая части левого собственного вектора-строки.
Приравнивая нулю действительные и мнимые части полных дифференциалов левых сторон приведенных уравнений получим:
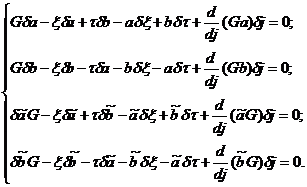(6)
Выполним над полученной системой преобразования имеем:
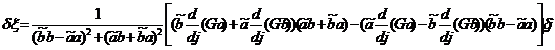, (7)
где вектор-строка:
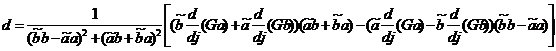, (8)
является вектором градиента, определяющим направление наискорейшего изменения значения 
. Обозначим номера всех собственных значений, при которых система неустойчива, т.е. 
>
. Представим векторы градиентов этих собственных значений в пространстве параметров 
в виде: 
Тогда малое приращение величины параметра 
вида 
позволит уменьшить значения, если только все 
имеют одинаковый знак, т.е., либо все положительны, либо все отрицательны. Тогда, можно уменьшить действительные части собственных значений, при которых система управления ПД неустойчива, до тех пор, пока они не станут отрицательными.
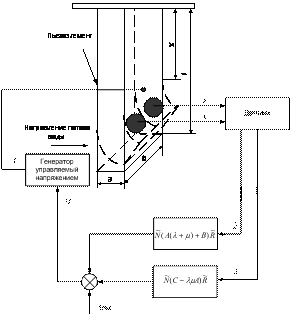
Рис. 1 – Система управления пьезоэлектрическим преобразователем с обратной связью
Данный подход позволяет синтезировать систему управления ПД, осуществляющую переход между двумя статическими положениями ПД с предписанным быстродействием и гашением «паразитных» колебаний.
Литература
1. Зенкевич, О. Метод конечных элементов в технике [Текст]. – М.: Мир, 1975. – 542с.
2. Бараускас, Р.А. Управление апериодическими движениями упругих механических систем [Текст]// Вибротехника. Межвузовский тематический сборник научных трудов, 1984 -№2(50).
3. Сэйдж, Э.П., Уайт, У.С. Оптимальное управление системами [Текст] / Под ред. Б. Р. Левина. - М.: Радио и связь, 1982. — 392 с, ил.
4. Сапронов, А.А., Зибров, В.А. Занина, И.А., Соколовская, О.В., Тряпичкин, С.А. Пьезоэлектрический генератор в устройстве мониторинга водопровода// Энергосбережение и водоподготовка. Научно-технический журнал, 2012. – №5 - С. 42-44.
5. Сапронов, А.А., Зибров, В.А., Занина, И.А., Соколовская, О.В.. Исследование процесса передачи информации по акустическому каналу в водопроводе [Текст]// Энергосбережение и водоподготовка. Научно-технический журнал, 2012. – №4. – С.52-54.