Имитационный подход к проблеме определения динамических характеристик средств измерений

Аннотация

В.П. Иосифов

Предложена методика определения полных динамических характеристик датчиков переменных давлений с применением имитационного подхода, основанного на добавлении в исходный отклик сигнала с известными параметрами.
Ключевые слова: средства измерений, датчики, динамические характеристики.

05.11.01 - Приборы и методы измерения по видам измерений

Постановка задачи.  Наиболее часто определение динамических характеристик средств измерений, в частности датчиков механических величин, проводится по откликам на известные воздействия. По полученному отклику, применяя методы параметрического спектрального анализа, можно найти параметры математической модели датчика, которые и соответствуют характеристикам самого датчика. При применении параметрических методов спектрального анализа последовательно оцениваются параметры математической модели для данного порядка и погрешность описания модели, а порядок выбирается по различным критериям, например критерии Акаике, критерии ФОП (финальное описание погрешности) и т.д. Применение этих критериев основано на использовании погрешности описания модели, а точнее оценки среднеквадратичного отклонения рассчитываемой математической модели от отклика. Но известно, что с повышением порядка уменьшается погрешность описания. Таким образом, чем выше порядок описываемой математической модели, тем точнее описание отклика этой моделью. Завышение порядка математической модели ведет к появлению несуществующих составляющих или к расщеплению одной из составляющих. Отсюда и возникает задача создания критерия или методики моделирования известного отклика с наименьшими погрешностями, причем погрешностями не только методического характера.
Имитационный подход.  Решим поставленную задачу следующим образом.
Пусть имеем отклик F, а также множество составляющих математической модели M, причем M=M{Y₁, Y₂,…, Y_p}, где Y_i - i-ая составляющая модели, p_и- истинный порядок модели. Основная задача это определение параметров Q (Q=Q(A_i, f_i,α_i, φ_i ), где A_i, f_i ,α_i,φ_i –амплитуда, собственная частота, декремент затухания, фаза i-ой составляющей модели) для модели M, с учетом того, что порядок p заранее не известен.
Запишем рассматриваемую задачу в символьном виде:
Дано:
x[i]-отсчеты для i=0÷(N-1),
N -количество отсчетов,
Dt -шаг дискретизации.
Необходимо найти порядок модели описания датчика -p и для каждого Yi

– параметры
, для n=1÷N

Дополним поставленную задачу еще одним условием:
Необходимо найти требуемые параметры с минимальной погрешностью.
При численном моделировании можно проверить насколько точно разработанная методика позволяет определять требуемые параметры. А при обработке реальных данных этого невозможно добиться.
Решению вышеприведенных трудностей и посвящена настоящая статья.
Предположим, что порядок математической модели известен. Тогда для оценивания авторегрессионных параметров (АР) параметров составим систему уравнений

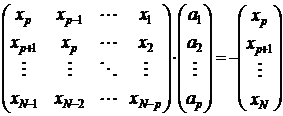
Главная сложность заключается в том, что заранее неизвестны ни порядок математической модели,  ни погрешность модели. А для выбора порядка модели применяется минимизация погрешности описания. При этом учитываются суммарное влияние всех составляющих, что затрудняет определение точности каждой из составляющих отклика.
Суть предлагаемой методики заключается в добавлении в искомый отклик составляющих с известными характеристиками Qд=Q(Aд fд, aд,φд ),

.

Добавлением составляющей Yд повышаем порядок математической модели на два: pд=p+2.
Для n=1÷N вычисляем

Далее применяем стандартную методику определения параметров, в том числе и порядка модели.
Для вновь полученной модели составляем систему уравнений

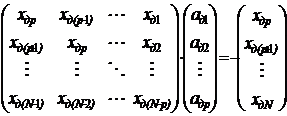
Параметры a={aд₁, aд₂, aд₃,…, aд_p} вычисляем, применяя метод наименьших квадратов.
Далее составляем и решаем характеристическое уравнение, корни которого соответствуют комплексным экспонентам.

   (4)

По найденным корням характеристического уравнения находим декременты затухания и собственные частоты экспоненциальных составляющих.

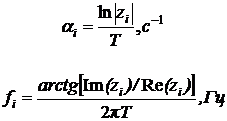
Для нахождения амплитуд и фаз составляются следующие уравнения:

.

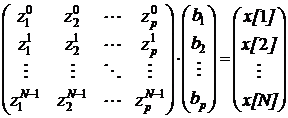Значения величин амплитуд и фаз вычисляются с помощью выражений

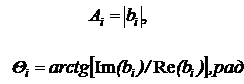
Добавка дополнительной составляющей выполняет роль калибровочного сигнала: мы имитируем добавление еще одной составляющей, но с известными характеристиками. И уже в ходе определения основных параметров математической модели имеем калибровочный сигнал, по вычислениям параметров которого можем и выбрать не только порядок вновь полученной модели, но и параметры рассчитываемой модели. Зная погрешности, по которым необходимо найти параметры математической модели, постепенно повышаем порядок модели до тех пор, пока не получим параметры калибровочного сигнала с требуемыми погрешностями.
Спектр сигнала  можно рассчитать следующим образом

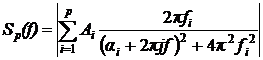
Применение вышеприведенных методов определения спектра пригодно для отображения спектров как узкополосных, так и широкополосных сигналов.
На рисунке 1 показан отклик датчика давлений ЛХ-610 серийный номер, №16578. Эксперимент производился на ударном стенде УУТ 5. Результаты получены с применением приведенной методики. В таблице приведены полученные результаты.

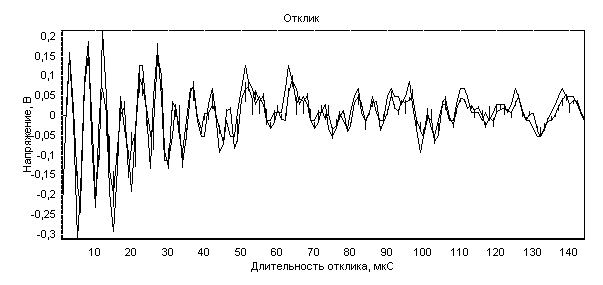
Рисунок 1. Отклик датчика ЛХ 610, №16578. Стенд УУТ 5.

Таблица 1. Результаты обработки отклика датчика.

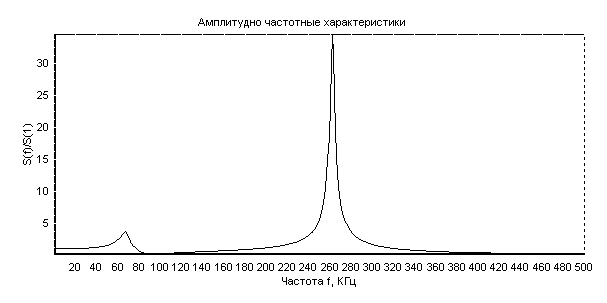
Рисунок 2. Амплитудно частотная характеристика датчика ЛХ 610

Заключение. В заключение необходимо отметить, что применение такого метода дает возможность   определение каждой из составляющих модели с требуемой точностью. При задании калибровочного сигнала необходимо придерживаться следующей технологии. Например, для датчиков, рабочий диапазон которых находится до первой собственной частоты, необходимо выбрать собственную частоту калибровочного сигнала меньшую, чем ожидаемая первая собственная частота самого датчика. Относительно декремента затухания калибровочного сигнала, его надо выбрать максимально ожидаемое. При определении динамических характеристик датчиков механических величин оценки декрементов затухания получаются завышенными по отношению к реальным декрементам.
В идеале можно добавить и калибровочный сигнал в виде суммы нескольких затухающих синусоид. Причем собственные частоты составляющих калибровочного сигнала необходимо будет разбросить по всему частотному рабочему диапазону.

Список использованной литературы.

1. М.А. Щербаков, В.П. Иосифов. Разработка методик обработки откликов с датчиков с короткой длительностью. Известия высших учебных заведений. Поволжский регион. Сер. Технические науки, 2006, №6, с.245-252.
2.М.А. Щербаков, В.П. Иосифов. Восстановление входного сигнала по результатам идентификации динамических характеристик СИ. Известия высших учебных заведений. Поволжский регион. Сер. Технические науки, 2007, №3, с.3-8.
3. Иосифов В.П. Разработка методов синтеза СИ с требуемыми динамическими характеристиками. Научно-технический журнал. Автоматизация, телемеханизация и связь в нефтяной промышленности. – М: ОАО «ВНИИОЭНГ», 2006.-№12. .-С.21-23
4.Иосифов В.П. Применение параметрических методов спектрального анализа в измерительных процедурах. Москва. Энергоатомиздат-2002г. 150 C.