Применение индекса фрактальной обработки кардиоинтервалограмм для анализа текущего состояния организма и мониторинга при диагностике
Аннотация
При использовании устройства хронодиагностики с биосинхронизацией позволит снизить воздействия, оказываемые на организм и повысить эффективность самого процесса. Это является не маловажным моментом на этапе терапевтического воздействия на организм человека, так как можно получить положительный результата при как меньшем количестве процедур. Это позволит создать более щадящие методы терапии. Метод основан на распознавании и измерении временных интервалов между R-зубцами ЭКГ. Обрабатывается полученный временной ряд с методом фрактальных параметров, а обработки получаемых данных непосредственно во время процедур поможет наилучшем образом подобрать само время проведения процедуры.
Ключевые слова: Хрономедицина, диагностика, RR-интервал, индекс фрактальной размерности, спектр временного ряда.05.11.17 - Приборы, системы и изделия медицинского назначения
Интерес к вопросам времени в медицине, биологии и экологии в последнее время существенно вырос. Хрономедицина ставит целью использовать закономерности биоритмов для улучшения профилактики, диагностики и лечения болезней человека. [1]
Поэтому при использовании устройства хронодиагностики с биосинхронизацией позволит снизить воздействия, оказываемые на организм и повысить эффективность самого процесса. Это является не маловажным моментом на этапе терапевтического воздействия на организм человека. Так может потребоваться для получения положительного результата значительно меньше не только самих процедур, но и количественное оказание данных процедур на организм человека. Это позволит создать более щадящие методы терапии.
Исключительно важная роль принадлежит методологии и методическим подходам, основывающимся на представлении о живом организме и текущих и нем процессах (как в норме, так и при патологии) в плане изменений всех функций во времени.
Так анализируя вариабельность сердечного ритма, как одного из таких процессов, можно оценить состояния механизмов регуляции физиологических функций в организме человека. Так же это дает картину об общей активности регуляторных механизмов не только сердца, но и других органов человека.
После съема данных и начала диагностического воздействия адаптационные реакции для каждого человека индивидуальны и реализуются с различной степенью участия тех, или иных функциональных систем, которые обладают в свою очередь обратной связью, изменяющейся во времени и имеющей переменную функциональную организацию. Метод основан на распознавании и измерении временных интервалов между R-зубцами электрокардиограммы (R-R–интервалы), построении динамических рядов кардиоинтервалов и последующего анализа полученных числовых рядов осуществляем с помощью применения индекса фрактальной размерности.[2]
Измерять длительность RR-интервалов можно аппаратным или программным путем. Проблема распознавания RR-зубцов электрокардиограммы в различных аппаратно-программных комплексах решается по разному. Представление динамических рядов кардиоинтервалов осуществляется в числовом виде для дальнейшего удобства обработки полученной информации.
Обрабатывается полученный временной ряд с учетом свойственных для него фрактальных параметров, прослеживаемых в каждом из ритмов человеческого организма, а обработки получаемых данных непосредственно во время процедур поможет наилучшем образом подобрать само время проведения процедуры. Для исследования временных рядов следует, для начала, вычислить какие-либо его фрактальные показатели. Однако фрактальная размерность временного ряда может быть вычислена непосредственно через клеточную размерность Dc. Для определения размерности Dc плоскость, на которой определен график временного ряда, разбивается на клетки размером δ и определяется число клеток N(δ) , где находится хотя бы одна точка этого графика. Затем меняется δ и в двойном логарифмическом масштабе строится график функции N(δ), который аппроксимируется прямой с помощью метода наименьших квадратов. Тогда Dc определяется по углу наклона этой прямой. Однако для надежного вычисления, как Dc, так и показателей H, υ , γ требуется слишком большой репрезентативный масштаб, содержащий несколько тысяч данных . Внутри этого масштаба временной ряд, как правило, меняет характер своего поведения много раз. Чтобы связать локальную динамику соответствующего процесса с фрактальной размерностью временного ряда необходимо определить размерность D локально. Для этого необходимо найти последовательность аппроксимаций, которая при фиксированном δ была бы в некотором смысле оптимальной. [3]
Произведем некоторые преобразования: умножим обе части ((1/ δ)D~N(δ)) на
1/δ и введем D под знак логарифма. В результате получим:
N(δ) ~ δ –D при δ → 0
Если теперь умножить обе части на δ2, то в данном случае определение размерности можно переписать в виде степенного закона для площади аппроксимаций S(δ) :
S(δ) ~ δ 2-D при δ → 0
Заметим, что такая форма в отличие от предыдущей не требует, чтобы симплексы, из которых состоит аппроксимация, были одинаковыми. Достаточно того, чтобы они имели один и тот же геометрический фактор δ . Это позволяет нам использовать аппроксимации, которые при фиксированном δ наилучшим образом покрывают график исследуемой функции.
Действительно, рассмотрим временной ряд, или график вещественной функции одной скалярной переменной y=f(t) , определенной на некотором отрезке [a,b]. Заметим, что мы можем рассматривать этот ряд как множество точек, погруженное в двумерное евклидово пространство. Для вычисления фрактальной размерности функции мы можем непосредственно использовать процедуру определения клеточной размерности. При этом покрытие клетками можно рассматривать как частный случай покрытия прямоугольниками. Покажем, что существует более точное покрытие графика функции y=f(t) из класса прямоугольников, нежели клеточное. Для этого введем равномерное разбиение отрезка
ωm = [a=t0<t1 <…< tm=b], δ =![]() ,
,
и построим минимальное покрытие функции f(t) в классе покрытий, состоящих из прямоугольников с основанием δ (рис.). Тогда высота прямоугольника на отрезке [ti-1,ti] будет равна величине Ai(δ) (разности между максимальным и инимальным значением функции f(t) на этом отрезке). Введем величину: ![]()
и назовем Vf(δ) амплитудной вариацией функции f(t) , соответствующей масштабу разбиения δ на отрезке [a,b]. Тогда полную площадь покрытия Sμ(δ) можно записать в виде
Sμ(δ) = Vf (δ) δ
Отметим, что Sμ(δ) является минимальной площадью покрытия графика из
класса прямоугольников. Поэтому назовем такое покрытие минимальным.
Далее из следует, что
Vf (δ) ~ δ –μ при δ → 0,
где
μ = Dμ – 1
Назовем показатель μ индексом фрактальности, а размерность Dμ размерностью минимального покрытия. Заметим, что эти величины являются центральными в данной работе. Чтобы соотнести Dμ с другими размерностями и, в частности, с клеточной размерностью Dc , построим клеточное разбиение плоскости графика функции f(t) как показано на рисунке 1. Пусть Ni (δ) - число клеток, покрывающих график f(t) внутри отрезка [ti=1, ti]. Тогда из рисунка 1 видно, что,
0 < N(δ)δ2 – Ai(δ) δ < 2 δ2
Разделим это соотношение на δ и просуммируем по i. В результате получим
0<N(δ) δ – Vf(δ)<2(b – a),
где ![]() сть полное число клеток размера δ, покрывающих график функции f(t) на отрезке [a,b]. Переходя к пределу при δ → 0, получим:
сть полное число клеток размера δ, покрывающих график функции f(t) на отрезке [a,b]. Переходя к пределу при δ → 0, получим:
N(δ) δ ~ Vf(δ) ~ δ-μ = δ1-D μ
С другой стороны
N(δ) δ = Sc(δ) δ-1 ~ δ1-Dc
Следовательно Dc = Dμ.
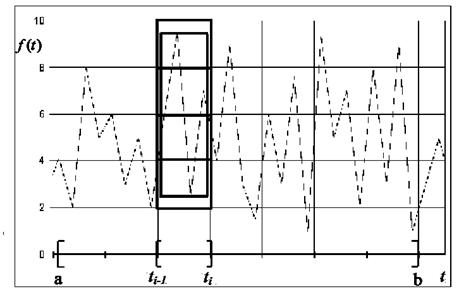
Рис. 1. Фрагмент клеточного (больший прямоугольник) и минимального (меньший прямоугольник) покрытий графика фрактальной функции на отрезке [ti-1,ti].
Из графика наглядно видно, что минимальное покрытие является более точным, нежели клеточное.
Отметим, однако, что для реальных фрактальных функций минимальные и клеточные покрытия могут давать весьма различные приближения величины S(δ) к асимптотическому режиму . Покажем, что эффект от этого может быть весьма ощутимым.
Поскольку Vf (δ) обычно имеет быстрый выход на асимптотический режим то соотношение может быть переписано в виде:![]() ,
,
где
0 < B(δ) < 2(b-a), D = Dc = Dμ , A = const
Здесь Aδ -D использовано вместо ![]()
где δ1 определено из соотношения ![]()
Поэтому ясно, что в этой области может существовать промежуточный режим со своим степенным законом, отличным от главного. Следовательно, при δ ≈ δ1 может существовать область «излома», где один степенной закон сменяется другим. Таким образом, это явление, которое весьма часто наблюдается на практике, иногда может быть связано исключительно с неточностью клеточных аппроксимаций. Кроме того, далее будет показано, что для графиков реальных временных рядов использование минимальных покрытий, вместо клеточных, позволяет существенно уменьшить количество данных, необходимое для определения фрактальной размерности и использовать индекс фрактальности m для локального анализа фрактальных временных рядов.
Индекс фрактальности можно использовать для традиционного анализа фрактальной структуры временных рядов. В частности, результаты анализа при помощи данных временных рядов при помощи μ совпадают с традиционными результатами, согласно которым показатель Херста для этих рядов обычно больше 0.5.
При одинаковом количестве данных индекс μ определяется в несколько раз точнее, чем показатель Херста H. При этом минимальный масштаб, необходимый для определения μ с приемлемой точностью составляет несколько десятков точек, тогда как для определения H необходимо несколько тысяч данных. Этот факт позволяет использовать μ в качестве локального фрактального показателя при анализе временных рядов.
Далее результаты обработки спектра временных рядов представляются в виде некой кривой линии как показано на рисунке 2, отражающей состояние организма, с отклонениями от нормы в случае ухода данной прямой вверх или вниз.
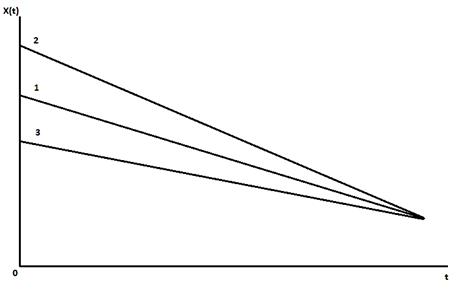
Рис. 2 Теоретическое представление спектра RR интервалов
Далее обрабатывая полученные результаты, можно получить картину распределения параметров состояния организма человека как показано на рисунке 2. Где схематически представлено как должен выглядеть график для здорового человека λ=1 – это соответстует нормальному состоянию организма (1), в сторону λ>1, то это характеризует перенапряжение (2), а если λ<1 – то соответственно угнетение этих систем (3).
Таким образом, исходя из полученной картины, можно не только наблюдать за оказываемым воздействие на организм больного, но и минимизировать процедуру, если кривая перейдет в нормальное состояние.
Литература:
1) Хильдебрандт Г., Мозер М., Лехофер М. Хронобиология и хрономедицина // биологические ритмы медицинское применение – М., 2006.
2) Д.м.н., профессор Баевский Р. М. Теоретические и прикладные аспекты оценки функционального состояния организма при действии факторов длительного космического полета – М. - октябрь 2005.
3) Старченко Н.В. Индекс фрактальности и локальный анализ хаотических временных рядов // Математическое моделирование, численные методы и комплексы программ – М., 2005.