Динамический выбор порядка в многоскоростном адаптивном фильтре
Аннотация
Дата поступления статьи: 28.10.2013Представлен новый способ настройки многоскоростного адаптивного фильтра. Основная идея заключается в возможности автоматического выбора порядка.
Мощность сигнала ошибки на выходе адаптивного фильтра эквалайзера можно представить в виде суммы двух составляющих: первая обусловлена усечением импульсной характеристики адаптивного фильтра, вторая составляющая представляет собой шум, возникающий в результате настройки весовых коэффициентов. Чем больше весовых коэффициентов, тем больше вносимый ими шум. В результате адаптивной настройки фильтр выбирает наилучший в смысле минимизации выходного шума порядок. Интерес представляет применение рассмотренного выше подхода в многоканальных эквалайзерах.
Благодаря введению процедуры динамического выбора порядков внутриканальных фильтров, удаётся значительно снизить вычислительные затраты на реализацию многоканального эквалайзера. За счёт уменьшения порядка адаптивного фильтра удаётся снизить отношение сигнал-шум в восстановленном эквалайзером сигнале.
Приводятся результаты компьютерного моделирования и временные диаграммы, характеризующие процесс выбора порядков адаптивных фильтров.Ключевые слова: адаптация, фильтр, многоскоростной, сигнал, динамический, порядок
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
Введение
Эквалайзеры широко применяются в системах передачи цифровой информации, канал связи в которых образован аналоговой передающей средой. Основная их функция состоит в компенсации межсимвольной интерференции, обусловленной неидеальностью и непостоянством частотных характеристик аналоговых каналов связи. В большинстве случаев эквалайзеры строятся на основе цифровых адаптивных фильтров и реализуются программно на цифровых сигнальных процессорах. Чаще всего разработчики стремятся использовать относительно простые алгоритмы адаптации, чтобы уменьшить вычислительные затраты и тем самым снизить энергопотребление и себестоимость выпускаемого устройства. Одним из наиболее известных адаптивных алгоритмов является нормированный алгоритм наименьшей среднеквадратической ошибки (НСКО) [1 – 3]. Если входной сигнал и обучающая последовательность адаптивного линейного сумматора являются стационарными, то среднеквадратическая ошибка (СКО) настройки, обусловленная ограничением порядка адаптивного фильтра, для алгоритма НСКО определяется выражением [2, 3]:
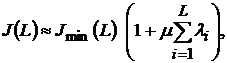
где ![]() — порядок адаптивного фильтра (длина воспроизводимой фильтром импульсной характеристики),
— порядок адаптивного фильтра (длина воспроизводимой фильтром импульсной характеристики), ![]() (
(![]() ) — собственные числа корреляционной матрицы входного сигнала,
) — собственные числа корреляционной матрицы входного сигнала, ![]() — шаг адаптации, изменяющийся в нормированном алгоритме НСКО обратно пропорционально мощности входного сигнала,
— шаг адаптации, изменяющийся в нормированном алгоритме НСКО обратно пропорционально мощности входного сигнала, ![]() — минимально достижимая ошибка настройки при использовании
— минимально достижимая ошибка настройки при использовании ![]() настраиваемых весовых коэффициентов. Если
настраиваемых весовых коэффициентов. Если ![]() — малая величина, то можно считать, что
— малая величина, то можно считать, что ![]() , и тогда увеличение порядка фильтра повышает точность настройки адаптивного фильтра. С ростом порядка фильтра растут вносимая им задержка, вычислительные затраты, постоянная времени адаптации. Поэтому неоправданное увеличение порядка адаптивного фильтра также нежелательно. В [4] для выбора оптимального порядка адаптивного фильтра был предложен критерий, основанный на поиске такого порядка, при котором наблюдается минимум отношения сигнал-шум на выходе эквалайзера.
, и тогда увеличение порядка фильтра повышает точность настройки адаптивного фильтра. С ростом порядка фильтра растут вносимая им задержка, вычислительные затраты, постоянная времени адаптации. Поэтому неоправданное увеличение порядка адаптивного фильтра также нежелательно. В [4] для выбора оптимального порядка адаптивного фильтра был предложен критерий, основанный на поиске такого порядка, при котором наблюдается минимум отношения сигнал-шум на выходе эквалайзера.
Теоретическое исследование
В предлагаемой ниже структуре используется несколько иной подход, основанный на сравнении двух сигналов ошибки. Допустим, что в некоторый момент времени ![]() (
(![]() — шаг дискретизации,
— шаг дискретизации, ![]() — дискретная переменная, определяющая моменты времени) порядок адаптивного фильтра равен
— дискретная переменная, определяющая моменты времени) порядок адаптивного фильтра равен ![]() . Ошибка восстановления в момент времени
. Ошибка восстановления в момент времени ![]() определяется для нормированного НСКО выражением [3]:
определяется для нормированного НСКО выражением [3]:
![]()
где ![]() — желаемый отклик фильтра (отсчёт обучающего сигнала),
— желаемый отклик фильтра (отсчёт обучающего сигнала), ![]() — комплексно-сопряжённый и транспонированный вектор весовых коэффициентов длиной
— комплексно-сопряжённый и транспонированный вектор весовых коэффициентов длиной ![]() ,
, ![]() — вектор отсчётов входной последовательности (сигнала, подлежащего восстановлению). Введём в рассмотрение «вложенный фильтр», который отличается от основного фильтра меньшим порядком:
— вектор отсчётов входной последовательности (сигнала, подлежащего восстановлению). Введём в рассмотрение «вложенный фильтр», который отличается от основного фильтра меньшим порядком: ![]() , где
, где ![]() — некоторая константа. По сути, этот фильтр отличается от лишь тем, что использует подмножество весовых коэффициентов основного фильтра. Введём в рассмотрение дополнительный сигнал ошибки:
— некоторая константа. По сути, этот фильтр отличается от лишь тем, что использует подмножество весовых коэффициентов основного фильтра. Введём в рассмотрение дополнительный сигнал ошибки:
![]()
Векторы ![]() и
и ![]() отличаются от
отличаются от ![]() и
и ![]() отсутствием крайних
отсутствием крайних ![]() элементов, то есть длина их меньше на
элементов, то есть длина их меньше на ![]() . Введём операцию усреднения двух сигналов ошибки по мощности:
. Введём операцию усреднения двух сигналов ошибки по мощности: 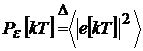 и
и 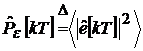 . На практике результаты усреднения определяются по некоторой конечной выборке. С учётом введённых выше обозначений правило выбора порядка адаптивного фильтра на очередной итерации можно выразить следующим соотношением:
. На практике результаты усреднения определяются по некоторой конечной выборке. С учётом введённых выше обозначений правило выбора порядка адаптивного фильтра на очередной итерации можно выразить следующим соотношением:
![]()
Введём для описанного адаптивного фильтра условное обозначение ![]() . Мощность сигнала ошибки на выходе адаптивного фильтра эквалайзера можно представить в виде суммы двух составляющих:
. Мощность сигнала ошибки на выходе адаптивного фильтра эквалайзера можно представить в виде суммы двух составляющих:
![]()
![]() обусловлена усечением импульсной характеристики адаптивного фильтра: чем больше усечения (чем меньше весовых коэффициентов, используемых фильтром), тем больше
обусловлена усечением импульсной характеристики адаптивного фильтра: чем больше усечения (чем меньше весовых коэффициентов, используемых фильтром), тем больше ![]() . Вторая составляющая
. Вторая составляющая ![]() представляет собой шум, возникающий в результате настройки весовых коэффициентов: чем больше весовых коэффициентов, тем больше
представляет собой шум, возникающий в результате настройки весовых коэффициентов: чем больше весовых коэффициентов, тем больше ![]() . В результате адаптивной настройки фильтр выбирает наилучший в смысле минимизации выходного шума порядок
. В результате адаптивной настройки фильтр выбирает наилучший в смысле минимизации выходного шума порядок ![]() .
.
Интерес представляет применение рассмотренного выше подхода в многоканальных эквалайзерах. Вопросы построения многоканальных эквалайзеров с адаптивным выбором порядков внутриканальных фильтров обсуждались в [5, 6]. Некоторые особенности настройки многоскоростных адаптивных фильтров (МАФ) с динамическим выбором порядков внутриканальных адаптивных фильтров удобно рассмотреть на примере.
Экспериментальное исследование
Проведём компьютерное моделирование, воспользовавшись пакетом «Simulink» программы «MATLAB». Пусть канал связи является стационарным и имеет замирание на некоторой частоте (рис. 1). Пусть МАФ разбивает сигнал на 4 равных по ширине полосы (рис. 2), причём замирание, как это следует из рисунка, приходится на третий канал МАФ. Временные диаграммы, характеризующие процесс выбора порядков адаптивных фильтров, показаны на рис. 3 и рис. 4, соответственно.
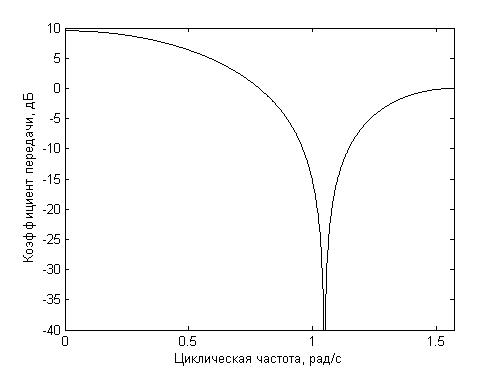
Рис. 1. – ЛАЧХ канала связи с замиранием
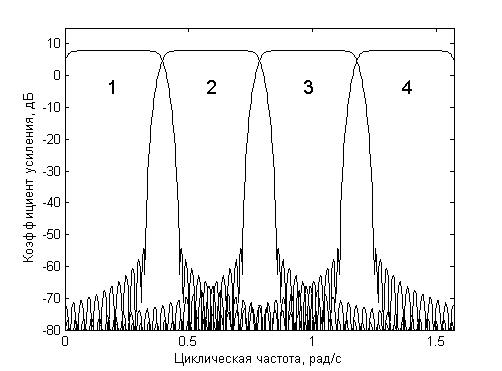
Рис. 2. – ЛАЧХ подсистемы фильтров анализа
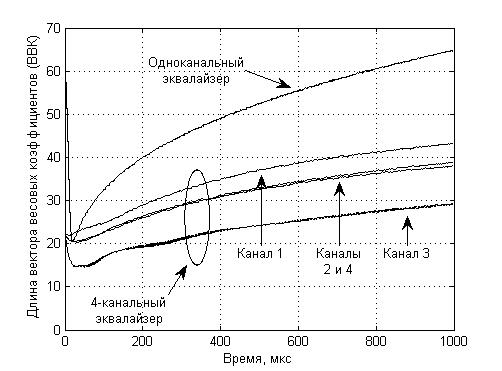
Рис. 3. – Процесс динамического выбора порядков одноканального адаптивного фильтра и 4-канального МАФ
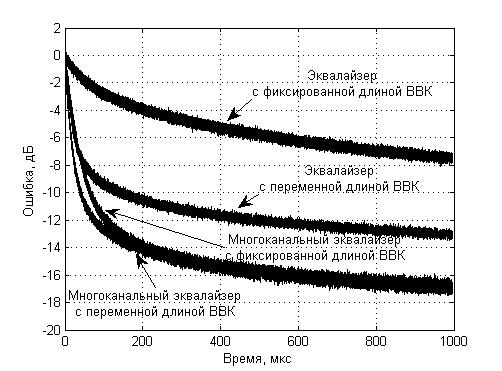
Рис. 4. – Уменьшение ошибки восстановления сигнала на выходе адаптивного фильтра эквалайзера (отношение сигнал-шум во входном сигнале выбрано равным 40 дБ)
На рис. 5 показана импульсная характеристика, полученная в результате настройки широкополосного (одноканального) эквалайзера 512-го порядка при отсутствии аддитивного шума в канале связи. Ниже выделен фрагмент этой импульсной характеристики, равный по ширине конечному значению длины ВВК, показанному на рис. 3.
Очевидно, что все характерные особенности желаемой импульсной характеристики содержатся в выделенном фрагменте.
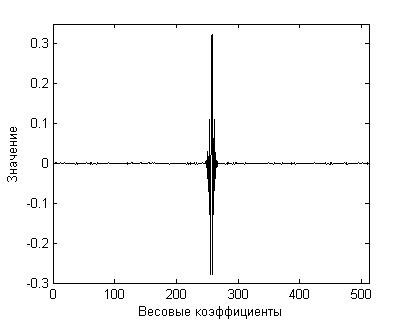
(а)
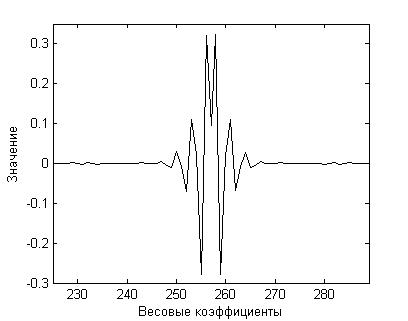
(б)
Рис. 5. – Импульсная характеристика МАФ после настройки
На рис. 6 показаны импульсные характеристики четырёх внутриканальных фильтров, полученные после окончания процесса настройки. Коэффициент усиления третьего канала МАФ оказался наибольшим, поэтому именно он вносит наибольший шум в восстановленный сигнал. За счёт уменьшения порядка адаптивного фильтра третьего канала (рис. 3) удаётся снизить отношение сигнал-шум в восстановленном эквалайзером сигнале.
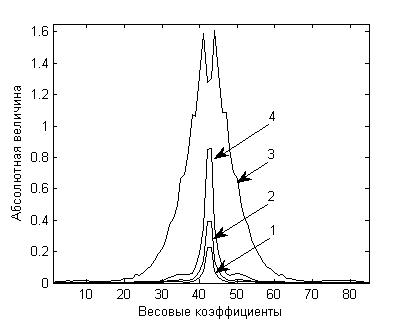
Рис. 6. – Импульсные характеристики четырёх внутриканальных фильтров, полученные после окончания процесса настройки
Выводы
Благодаря введению процедуры динамического выбора порядков внутриканальных фильтров, удаётся значительно снизить вычислительные затраты на реализацию МАФ. Перспективные исследования в данном направлении связаны с применением подобных МАФ в системах типа [9, 10].
Литература:
- Уидроу Б. и др. Комплексная форма алгоритма НСКО [Текст] // ТИИЭР. 1975. – № 3. – С. 49 – 51.
- Уидроу Б., Стирнз С. Адаптивная обработка сигналов [Текст] / пер с англ. – М.: Радио и связь, 1989. – 440 с.
- Haykin S., Adaptive filter theory [Текст], 4th ed. – NJ: Prentice-Hall, 2001. – 936 pp.
- (WO 98/15901) System for dynamically adapting the length of a filter [Текст], 16.04.1998 G06F 17/10, H04B 3/23, H04M 9/00 PCT/IL97/00315 COMSYS COMMUNICATION & SIGNAL PROCESSING LTD.
- Vityazev V.V., Linovich A. Yu. Flexible Time-Frequency Decomposition in Subband Equalization” [Текст] // 17th Telecommunications forum – TELFOR 2009, Serbia, Belgrade, November 24-26, 2009. – p. 540 – 543.
- Линович А.Ю. Многоканальный адаптивный фильтр на основе алгоритма NLMS с настраиваемой структурой системы анализа-синтеза [Текст] // Методы и устройства формирования и обработки сигналов в информационных системах: Сбор. науч. тр. / Под ред. Ю.Н. Паршина. – Рязань: РГРТУ, 2010. – С. 47 – 52.
- Линович А.Ю. Многоканальные эквалайзеры с самоорганизующейся структурой [Текст] // Материалы конференции «Современные проблемы радиотехники и телекоммуникаций «РТ-2011», Севастополь, 2011. – С. 352.
- Vaidyanathan P.P., Multirate systems and filter banks [Текст], NJ: Prentice Hall, 1993. – 1450 pp.
- Колесников С.В., Зайцева Т.В., Рогожкина А.Ю., Ушаков С.А., Комиссаров А.В. Влияние пространственной структуры активной антенной решетки на угловые спектры мощности интермодуляционных помех [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4, ч. 2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1468 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Воропай М.Н., Иванов С.В. Синтез структуры и реализация широкополосного радиоприемного устройства в диапазоне рабочих частот 0,02… 18,00 ГГц для комплексов радиомониторинга [Электронный ресурс] // «Инженерный вестник Дона», 2010, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2010/194 (доступ свободный) – Загл. с экрана. – Яз. рус.