Синтез адаптивного регулятора шкворневого узла

Аннотация

А.А. Демьянов, Б.И. Павлицкий, C.А. Шапшал

Дата поступления статьи: 24.10.2013

Представлено решение важной отраслевой проблемы повышения  безопасности движения подвижного состава путем снижения бокового износа гребней колес и головок рельсов при вписывании тележек в кривые участки пути за счет повышения надежности и долговечности шкворневого узла. Для решения этой задачи в статье предложено оригинальное конструкторское решение дозированной подачи смазки к фрикционным поверхностям деталей по мере износа их контактирующих поверхностей. Согласно предложенному решению на фрикционных поверхностях шкворневого узла выполняются выемки, заполненные твердым композиционным смазочным материалом, который по мере износа будет порциями попадать в область контакта. Разработаны теоретические основы и уравнение адаптивного управления этим процессом.  

Ключевые слова: Пятниковый узел, адаптивный регулятор, рабочие характеристики, смазочный слой, износ

05.22.07 - Подвижной состав железных дорог, тяга поездов и электрофикация

Одной из основных причин бокового износа гребней колёс и головок рельсов является резкое ухудшение состояния узла пятник-подпятник вагонных тележек модели 18-100, приводящее к росту угла набегания колеса на рельс и направляющих движение экипажа в колее сил. При эксплуатации в условиях перевалки кузова на пятнике или завале на скользуны вследствие "открытости" конструкции узлов опирания смазка из зон контакта постепенно выдавливается, а процесс взаимодействия между сопрягаемыми поверхностями приобретает характер сухого трения. Это приводит к интенсивному неравномерному износу трущихся поверхностей и изменению величины суммарных зазоров по скользунам. В результате такой работы узла происходит изменение динамических показателей грузового вагона и параметров тележки модели 18-100 в плане, что в конечном итоге определяет величину угла набегания колеса на рельс и величины сил взаимодействия в зоне контакта колеса и рельса.
Одним из перспективных способом решение проблемы повышения долговечности, снижения интенсивности износа упорной и опорной поверхностей пятника и подпятника является реализация принципов адаптации в механических системах [1, 2, 6, 7]. В настоящее время известна конструкция адаптивной системы шкворневого узла. Особенностью конструкции является то, что на упорной и опорной поверхностях пятника и подпятника предусмотрены выемки, заполненные композиционным смазочным материалом. Глубина выемок не превышает величины допустимого износа [1, 2].
Принцип работы адаптивной системы состоит в следующем: при скольжении пятника относительно подпятника по мере изнашивания рабочей поверхности в зону контакта будет попадать смазка, за счет того, что в них имеется глухие отверстия, заполненные смазочным консистентным материалом. В результате в зону контакта будет попадать смазка, которая покроет поверхности трения и снизит интенсивность износа [1, 2, 9, 10].
В общепринятой форме решение задачи построения адаптивного регулятора сводится к идентифицированию его параметров в форме “вход-выход”, при этом необходимо ответить на три основных вопроса [3, 4, 5]:

1. Идентифицировать параметры объекта управления;
2. Синтезировать алгоритм работы регулятора, при известных параметрах объекта обеспечивающих требуемое качество работы системы;
3.  Конструирование (синтез) регулятора реализующего этот алгоритм.

Однако, как видно из описания работы предлагаемой конструкции шкворневого узла его параметры изменяются во времени и, следовательно, эти задачи необходимо решать в темпе процесса его функционирования. Таким образом, алгоритм регулятора должен изменятся в рамках этого процесса, адаптируясь за некоторое время к изменяющимся параметрам объекта, так чтобы уровень его работы соответствовал заданному.
Анализ работы шкворневого узла позволяет сделать эвристическое заключение о том, что решение таких задач в приложении к исследуемому объекту целесообразно решать, используя функционально-адаптивные системы управления [3, 4, 5] в которых изменение параметров регулятора формируется непосредственно из целей управления.
Исходя из выше сказанного, рассмотрим особенности построения адаптивных механических систем, вектор управления возмущенного движения которых описывается уравнением:

.(1)

где     – мерный вектор переменных состояний объекта;
 – мерный вектор управления.
В развернутой форме уравнение (1) имеет вид:

.

где     – заданные функции, которые предполагаются непрерывными и необходимое число раз дифференцируемыми по .
В уравнении (1) управление и состояние объекта являются неизвестными функциями по времени, которые определяются из следующих условий. Задано начальное () и конечное () состояние объекта (1):

; (2)

.(3) где     – время начала функционирования объекта;
 – время окончания функционирования объекта.
Эффективность управления оценивается с помощью интеграла:
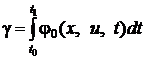(4).

где     – заданная непрерывная функция своих аргументов.
В зависимости от характера решаемой задачи, эффективность управления может оцениваться либо по уменьшению значения этого интеграла, либо по его увеличению. Для упрощения решаемой задачи будем полагать, что эффективность управления тем выше, чем меньше значение этого интервала.
На управления и переменные состояния накладываются ограничения, выражающие ограниченные ресурсы управления и допустимые пределы изменения переменных состояния, с учетом положений предыдущего пункта имеющих вид:

.

где    – заданные числа.
В общем случае будем считать, что в соответствии с конструктивными особенностями объекта и условиями его эксплуатации заданно замкнутое множество  в пространстве переменных  и управления могут принимать в каждый момент времени лишь значения из этого множества. Замкнутость множества  означает, что управление содержится не только внутри, но и на его границе т.е. .
Однако реальное движение системы имеет более сложный и не однозначный характер, что вызвано следующими причинами:
- неточная реализация начальных условий (2), (3);
- неполная информация о внешних возмущениях, действующих на систему;
- неточная реализация процесса управления.
В результате этого реальное движение описывается функциями, учитывающими эти обстоятельства. Иными словами необходимо получить уравнения возмущенного (реального) движения, описывающее отклонение от уравнения невозмущенного (теоретического) движения. Задачи такого рода, в общем виде, решаются следующим образом [3, 4].
Пусть уравнение невозмущенного движения найдено, т.е. функция  известны. Очевидно, что, подставляя их в уравнение (1) и решая его с начальными условиями (2), (3) получим . Таким образом, для получения реального движения необходимо ввести функции возмущения (отклонения).
Если  и  – отклонения, соответственно, реального движения и управления от теоретического, то возмущенное движение системы описывается функциями:

; ; . (5)

Числа  являются случайными, но достаточно малыми величинами, значения которых неизвестно, но по условию уравнения их диапазон изменения не должны превышать некоторого заданного  значения т.е. удовлетворять неравенству:

.

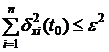После этого, целесообразно выразить эффективность управления (4), не как функцию времени, а как функцию переменных состояний при возмущенном движении системы:

.

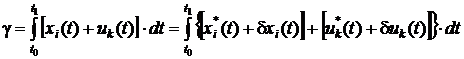Отсюда, решение задачи будет заключаться в минимизации функционала (5) в интервале  т.е.:
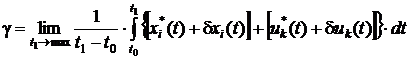. (6)

Таким образом, исходя из принципов аналитического конструирования регулятора, требуется найти матрицу чисел с размером  уравнения регулятора, обеспечивающую устойчивое движения объекта управления возмущенное движение, которого в первом приближении можно описать уравнением в матричной форме:
.

Зависимость параметров регулятора от параметров состояния объекта может быть как аналитической, т.е. заданной с помощью формул, так и алгоритмической, с помощью которой для каждого фиксированного состояния можно найти матрицу векторов управления [3, 4]. При достаточно ограниченной информации об особенностях функционирования шкворневого узла с адаптивным регулятором реализация первого подхода к решению задачи не предоставляется возможным, поэтому реализация второго подхода к ее решению является предпочтительным. В связи с этим целесообразно рассмотреть параметры состояния и адаптивного управления ни как явные функции времени, а как функции переменных состояний и управления не зависящих от начальных условий из множества (5) имеющих соответственно следующий вид:

; (7)

. (8)

Поскольку функция управления включает неопределенные значения параметров, для которых определены только ограничения, структура адаптивных систем предполагает наличие функции, включающей критерий изменения неопределенных параметров:

. (9)

В данном случае уравнения (7), (8) описывают алгоритм работы регулятора, а уравнение (9) описывает алгоритм адаптации, где  системный элемент, реализующий алгоритм адаптации называемый адаптером [3].
Таким образом, адаптивный регулятор будет состоять из регулятора и адаптера. Типовая схема, реализующая этот принцип, представлена на рисунке 1. Естественно, что с учетом условия минимизации  функционал (6), реализуемый по этой схеме регулятора и задаваемого через функцию (7), (8) переменных состояний должен обладать свойствами:

.(10)

После этого перейдем к решению задач поставленных вначале раздела.

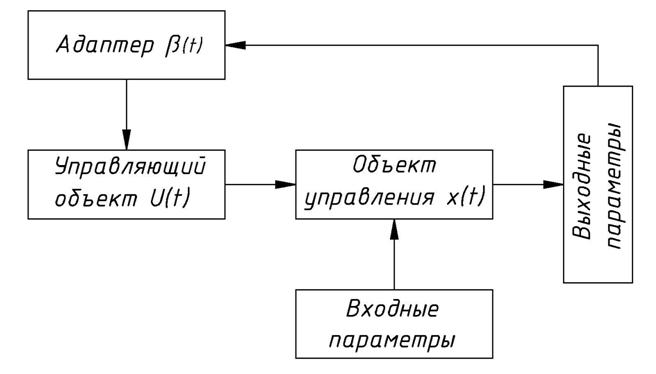
Рис. 1. – Функционально-структурная схема адаптивной системы.

Первая задача. Идентификация параметров объекта управления в форме «вход-выход». В нашем случае должна включать и терминологическую идентификацию теории адаптивного управления в приложении к механической системе с учетом особенностей шкворневого узла.
Как следует из описания принципа работа шкворневого узла толщина смазочного слоя  является функцией конструктивно-эксплуатационных параметров. В свою очередь от значения параметров  «включается» или «отключается» механизм подачи смазки, что непосредственно влияет на величину износа  и, следовательно,  функция .

,

но  можно выразить через время  интенсивности  износа:

,

и, следовательно:

. (11)

Если выразить  как функцию времени , которая определяет интенсивность износа:

,

то можно записать (11) так:

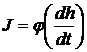. (12)

Задавая аргумент функции (12) через функцию состояния:

,

получим:

. (13)

С другой стороны  будет определятся нагрузочно-скоростным режимом, и состоянием контактирующих поверхностей пятника и подпятника. В данном случае имеется ввиду наличие или отсутствие разделительного слоя. Однако состояние поверхности характеризуется коэффициентом трения, который является функцией типа материалов , твердость  и шероховатости сопряженных поверхностей, а также наличие или отсутствия  загрязнителей, типа  смазочного материала и толщина  смазочного слоя:

.

Если учесть, что  являются величинами постоянными для принятой конструкции узла, а  изменятся в диапазоне характерным для конструктивного исполнения и условий эксплуатации узла, то можно считать  функцией :

.

Таким образом, в нашем случае  реализует алгоритм адаптации, являясь по терминологии теории адаптивного управления адаптером. Соответственно  и  будет характеризовать переменные состояния и управления. Таким образом, можно записать:

.(14)

Обобщив полученные результаты (14) выразим уравнение управления объекта (13):

,

ограничения (2), (3):

;
.

и уравнения (9):

.

С учетом выполненной идентификации.
Вторая задача. Для решения задачи синтеза алгоритма работы регулятора шкворневого узла представим уравнения (7) и (8) учитывая (14) в виде:

; 16

.

В результате решение задачи будет заключаться в минимизации функционала (10) представленного в виде:

.

Третья задача. Задача синтеза адаптивного регулятора в общепринятой постановке [3] с учетом конструктивных и эксплуатационных особенностей шкворневого узла будет состоять в определении по уравнению объекта (16), множеству  и цели  алгоритма адаптации и регулирования, которые согласно раннее выбранного подхода реализуются путем составления функционально-структурной схемы, позволяющей для любого вектора значений  и любых начальных условий  достигать цели управления.
Возможность решения этой задачи зависит, прежде всего, от цели управления, при задании которой необходимо учитывать уровень (объем) априорной информации об объекте возмущения [1, 3, 6, 7, 8]. Очевидно, что при решении задачи в приведенной формулировке необходимо определять взаимосвязь между параметрами внешний воздействий ,  на объект управления системы «пятник-подпятник» и параметрами адаптации управления.
Параметры шкворневого узла с адаптивным регулятором представлены в таблице 1 и на функционально-структурной схеме (рисунок 2).
Таблица 1
Адаптивный регулятор шкворневого узла

Система

Режим

Условия управления

Адаптер

Включение. Отключение. Устойчивый.

Управляющий объект (система подачи смазки)

Включение. Отключение. Устойчивый.

Выход

Включение. Отключение. Устойчивый.

Вход

Таким образом, получены теоретические основы и методология синтеза адаптивного регулятора механических систем в приложении к шкворневому узлу.

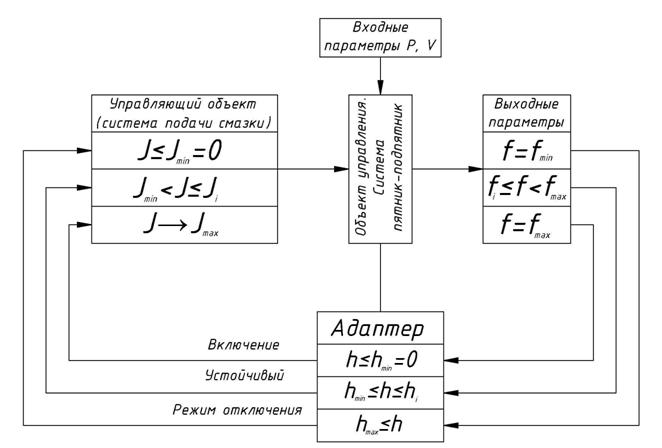
Рис. 2. – Функционально-структурная схема шкворневого узла с адаптивным регулятором

Список литературы:

1. Павлицкий, Б.И. Особенности адаптивного управления подачей смазки в шкворневом узле / Б.И. Павлицкий // Вагоны и вагонное хозяйство. – Москва, 2013. – №3. – С. 48.
2. Шкворневая система устройства, перемещающегося по рельсам: патент 2389627 Рос. Федерации: 6 B61F 5/00 / А.А. Демьянов. – № 2008101712/11; заявл. 16.01.2008; опубл. 20.05.2010, Бюл. № 14 – 7 с.
3. Александров, А. Г. Оптимальные и адаптивные системы / А.Г. Александров. – М.: Высшая школа, 1989. – 263 с.
4. Narendra K.S., Valavani L.S. Stable adaptive controller design – direct control // IEEE Trans. on Automat. Control. – 1978. – Vol. 23, No. 4. – P. 570-583.
5. Parks, P.C. Lyapunov redesign of model reference adaptive control system // IEEE Trans on Autom. Control. – 1966. Vol. 11. No. 3. – P. 362-367.
6. Демьянов, А.А. Адаптивный синтез фрикционно-механических систем. / А.А. Демьянов, Ал.А. Демьянов // Труды международной научно-практической конференции «Проблемы и перспективы развития транспортного комплекса» / РГУПС – 2009. с.44-45.
7. Демьянов, А.А. Метод адаптивного синтеза фрикционных систем / А.А. Демьянов, Ал.А. Демьянов. – М.: Энциклопедия Машиностроения, 2008. – с.72-74.
8. Шанин, Д.А. Нейросетевой адаптивный контроллер для задачи управления объектом с неизвестной структурой посредством глобальной обратной связи [Электронный ресурс] // «Инженерный вестник Дона», 2008, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2008/60 (доступ свободный) – Загл. с экрана. – Яз. рус.
9. Мантурова, Е.А. Применение наноматериалов и нанофункциональных присадок в перспективных технологиях лубрикации контакта гребня колеса с боковой поверхностью головки рельса [Электронный ресурс] // «Инженерный вестник Дона», 2010, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2010/197 (доступ свободный) – Загл. с экрана. – Яз. рус.
10. Дерлугян, Ф.П. Обоснование процесса получения композиционных антифрикционных самосмазывающихся материалов с заданными техническими характеристиками методом химического наноконструирования [Электронный ресурс] // «Инженерный вестник Дона», 2010, №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2010/287 (доступ свободный) – Загл. с экрана. – Яз. рус.