Методика расчета силовой характеристики ленточного упругопластического элемента

Аннотация

Б.М. Языев, И.И. Смирнов, К.В. Захарова

Дата поступления статьи: 04.12.2013

В настоящее время активно развивается направление сейсмозащиты, связанное с использованием энергопоглощающих экранов, выполненных в виде трехслойных конструкций с упругопластическими энергопоглощающими элементами. В данной статье, на основании проведенного исследования и анализа, выведены формулы расчета силовой характеристики ленточного упругопластического элемента.

Ключевые слова: Динамическая нагрузка, упругопластическая деформация, диаграмма деформирования, энергопоглощение

05.23.17 - Строительная механика

08.00.05 - Экономика и управление народным хозяйством (по отраслям и сферам деятельности)

Ранее было отмечено [1, 2], что для защиты зданий и сооружений эффективнее других использовать системы на основе упругопластических энергопоглощающих элементов (УПЭ). Для расчета систем защиты с такими элементами необходимо знать их силовую характеристику. Следует отметить, что попытки достаточно точно представить характеристики УПЭ на диаграммах «деформация-сила», «скорость деформации-сила» не имеют успеха. В силу несправедливости гипотезы о разделении упругой и диссипативной составляющих.
В данной работе рассмотрена принципиально новая конструкция пластического амортизатора - амортизатор, содержащий в качестве рабочего пластического элемента ленту, перекатывающуюся в постоянном зазоре (рис. 1).
В связи с тем, что конструктивное исполнение рассматриваемого амортизатора  является новым и для него отсутствуют методики расчета силовой характеристики, то в настоящей статье  проанализированы основные физические и геометрические соотношения, на основе которых получены аналитические выражения для расчета силовой характеристики.

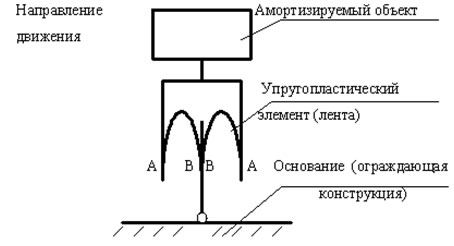
Рис. 1. Схема амортизатора

При расчете считаем, что система имеет одну степень свободы[4]

             (1)                                                     
где х – смещение амортизируемого объекта относительно ограждающей    конструкции;                                                                                
σ (t) – внешнее воздействие;
– алгоритм расчета f по или динамическая характеристика упругопластического элемента.
При расчете  выделяется этап упругого деформирования и этап пластического перекатывания ленты. На упругом этапе предполагаем, что деформируется только цилиндрический участок ленты (рис. 2, а).

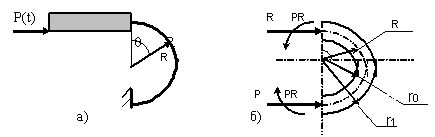
Рис. 2-Схема работы амортизатора

В результате имеем плоскую задачу теории упругости (рис. 2, б) [5, 6].
Решая ее, получим:

σ_r =     (2)                                                 
σ_q = ;    (3)                             
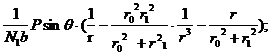τ_{rq = -   (4)                           
где N1 = ln ;}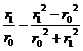       

Тогда      u_z =   (5)                                              
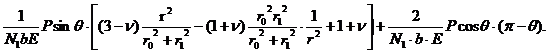u_q=     (6)

Если размеры сечения упругопластического элемента малы по сравнению с радиусом кривизны, то можно перейти к приближенному решению:
σ_q     =   (7)                                                             

                                                                    
τ_rq =   (8)                                                      
u_r =      (9)                                                     
u_q =    (10)                                          
где M = P∙R∙cos q - изгибающий момент в сечении q;
Q = P∙sin q - поперечная сила в сечении q;
z = r – R;        δ = r₁ – r₀;
J =  - момент инерции сечения.
При динамическом нагружении значение предела текучести зависит в общем случае от предыстории нагружения и не будет одинаковым по сечению. Предельная динамическая эпюра σ_{q пр} изображена на рис. 3, а.

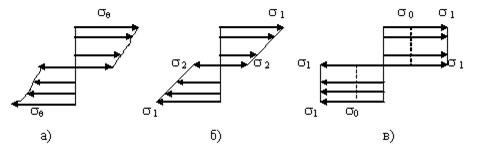
Рис. 3-Эпюры нагружений

Предельный момент по эпюре σ_{q пр} определится выражением:
М пр = 2 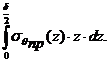  (11)                                          
Зависимость между пределом текучести и средней скоростью деформации примем в виде / 5 /:
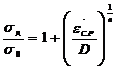,  (12)                                                      
где  σд _– динамический предел текучести;

D, n – константы материала;

       – средняя скорость деформации.
Запишем зависимость в более удобном виде:
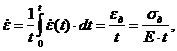=     (13)                                         
где ε_д – значение деформации в момент достижения динамического предела      
текучести.
Подставляя зависимость (3) в (2), получим:
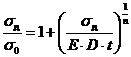,  (14)                                                     
Расчет упругопластического элемента велся в два этапа: сначала при динамическом нагружении эпюра σ_q полагалась такой, как показано на рис. 3б, а при появлении пластического шарнира – как показано на рис. 3в. Напряжение σ₁ соответствует моменту времени t1 появления пластического состояния во внешних волокнах ленты. Напряжение σ₂ – напряжение в среднем волокне ленты. Пластическое состояние в среднем волокне достигается в момент времени t₂. Ясно, что t₂>t₁.
При заданном законе нагружения P(t) можно определить t₁, σ₁, t₂, σ₂.[7, 8]
Для сечения q = 0 в момент времени t₁ имеем:
M (t₁) = P (t₁)∙ R = σ₁ ,  (15)                                         
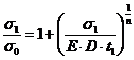.  (16)                                                   
Отсюда определяются t₁ и σ₁.
В момент времени t₂ имеем:
M (t₂) = P (t₂) ∙R = ,  (17)                                
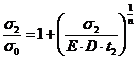.   (18)                                               
Отсюда определяются t₂ и σ₂ .
С появлением пластического шарнира расчетная схема (см. рис. 2, а) перестает отражать реальное поведение упругопластического элемента (см. рис. 1), так как не учитывает возможность перекатывания ленты. В первом приближении при расчете усилия в элементе определяем М пр и на всем дальнейшем участке перекатывания полагаем М=М_пр. Предельная сила сопротивления элемента при этом будет равна Р _пр = М _пр / R .
Понятно, что сопротивление УПЭ на этапе перекатывания изменяется, так как шарниры пластичности образуются при различных скоростях деформации [9, 10]. Для учета этого явления был проведен уточненный расчет силы сопротивления элемента. Этот расчет проводился в предположении, что предельная эпюра имеет вид, изображенный на рис. 3, в. С учетом сказанного имеем:
Р _пр (t) =  ,    (19)                                                
где Р_пр(t) – сила сопротивления упругопластического элемента на этапе перекатывания;
Напряжение σ₁ определяется из уравнения:
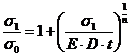,       t≥t₂ . (20)

                                            
Литература:

1. Смирнов И.И., Захарова К.В., Авилкин В.И., Стрельников Г.П. К  использованию торсионных энергопоглотителей для сейсмозащиты сооружений [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1314 (доступ свободный) – Загл. с экрана. – Яз. рус.
2. Смирнов И.И., Захарова К.В. К расчету упругопластических торсионов энергопоглощающих устройств [Электронный ресурс]  // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1312 (доступ свободный) – Загл. с экрана. – Яз. рус.
3. Смирнов И.И., Захарова К.В. Обоснование конструктивных особенностей энергопоглотителей для сейсмозащиты сооружений [Электронный ресурс]  //  «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа http://www.ivdon.ru/magazine/archive/n4p2y2012/1313 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Батуев Т.С. и др. Инженерные методы исследования ударных процессов. М.: Машиностроение, 1977. с.240
5. Лурье А.И. Теория упругости. М.: Наука, 1970. с.480
6. Тинг У. Пластическая деформация консольной балки из чувствительного к скорости деформирования материала при импульсном нагружении. Прикладная механика, 1964, № 1 с.5
7. Андреев В.И., Потехин И.А. Моделирование равнопрочного цилиндра на основе итерационного подхода// International Jornal for Computational Civil and Structural Engineering, v. 4, is. 1, 2008, p. 79-84
8. Формалев В.Ф., Ревизников Д.Л. Численные методы.- М.: ФИЗМАТ-ЛИТ, 2004. с.400
9. Andreev V.I. Minaeva A.S. Creation on the basis of the first theory of strength model equal stressed cylinder exposed to power and temperature loads. International Journal for Computational Civil and Structural Engineering. Volume 7, Issue 1, 2011. p. 71-75
10. Andreev V.I.  Optimization of thick-walled shells based on solutions of inverse problems of the elastic theory for inhomogeneous bodies. Computer Aided Optimum Design in Engineering XII (OPTI XII). WIT  Press. 2012, p.189-201