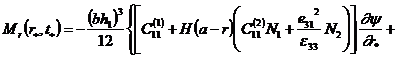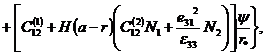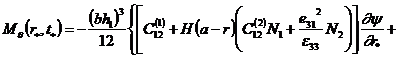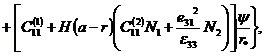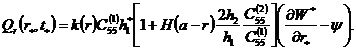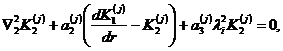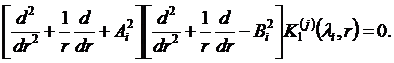Вынужденные осесимметричные колебания тонкой круглой биморфной пластины ступенчато переменной толщины и жесткости

Аннотация

Д.А. Шляхин

Дата поступления статьи: 14.12.2012

Рассматривается  нестационарная осесимметричная  задача  для  тонкой  биморфной пластины  при  действии на торцевой  поверхности  нормальных напряжений, являющихся произвольной функцией радиальной координаты времени и времени . На основании теории Тимошенко методом конечных  интегральных преобразований построено новое замкнутое решение для рассматриваемой электроупругой системы ступенчато переменной жесткости и толщины. Полученные расчетные соотношения позволяют исследовать напряженно-деформированное состояние и величину разности потенциалов между лицевыми электродами  биморфных элементов.

Ключевые слова: задача прямого пьезоэффекта, тонкая биморфная пластина, осесимметричная динамическая нагрузка

01.04.06 - Акустика

05.23.17 - Строительная механика

1.Введение.

В различных акустических устройствах в качестве преобразователя энергии используются тонкостенные круглые биморфные пластины. Наиболее эффективной конструкцией, обладающей высокой механической прочностью и чувствительностью, является круглая металлическая подложка с наклеенными с двух сторон пьезокерамическими пластинами меньшего диаметра. Расчет рассматриваемых тел вращения, как правило,  выполняется путем аппроксимации их набором кольцевой и сплошной пластин постоянной толщины. При этом для определения напряженно-деформированного состояния каждого элемента используется техническая теория тонких пластин [1-3].
В настоящей  работе  исследование  тонкой  биморфной пьезокерамической пластины проводится на основании гиперболической системы уравнений Тимошенко [ 4 ], в которой  ступенчато переменная толщина и жесткость системы, а также нестационарная механическая нагрузка описывается с помощью сингулярных обобщенных функций [ 5 ]. Кроме того, по-видимому, впервые в настоящей работе при решении динамических задач учитывается особенность изменения, в виде скачка, градиента касательных и нормальных  напряжений в области изменений  высоты и жесткости пластины.  При  исследовании задачи на собственные значения для тонких пластин ступенчато-переменной толщины данная особенность учитывалась в работе [ 6 ].
2.Постановка задачи.

Пусть биморфная круглая пластина  состоит из металлической заземленной подложки, занимающей  в  цилиндрической  системе  координат   область  :   , и двух наклеенных на нее пьезокерамических элементов меньшего диаметра  толщиной  (рис.1 ). Изгибные осесимметричные колебания возбуждаются за счет действия механической динамической  нагрузки   ( нормальных   напряжений )   ,  являющейся  произвольной

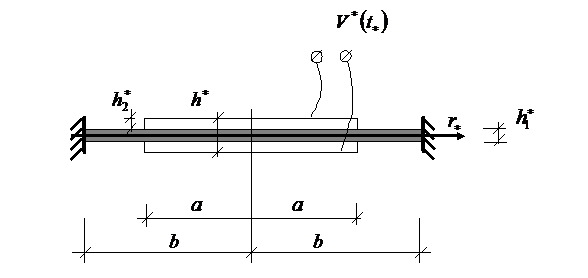
Рис.1. – Биморфная пластина

функцией радиальной координаты  и времени . В результате деформирования  на лицевых  электродах  пьезокерамических  пластин  генерируется  электрический  потенциал  . Подключение их к измерительному прибору позволяет зафиксировать величину и форму электрического напряжения .
Условия закрепления цилиндрической поверхности пластины могут быть произвольными. Для определенности считаем ее жестко закрепленной.
Система Тимошенко для рассматриваемой тонкой круглой пьезокерамической биморфной пластины в безразмерной форме записывается в виде следующих дифференциальных уравнений осесимметричного движения и начально-краевых условий:

где  ,   прогиб и угол поворота сечения пластины  в плоскости ,     ,   

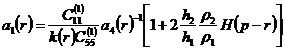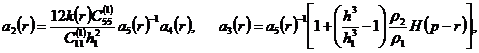
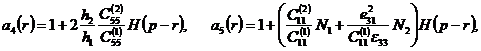
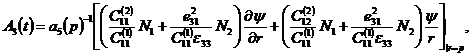
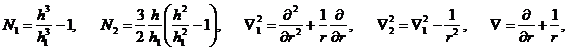
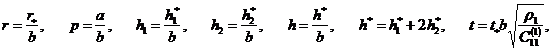
 объемная плотность и модули  упругости соответственно  металлической подложки и пьезокерамических пластин;    пьезомодуль и диэлектрическая проницаемость электроупругого  материала; коэффициент поперечного сдвига;  известные в начальный момент времени перемещение, угол поворота и их скорости; единичные функции Дирака и Хэвисайда.
В равенстве ( 3 ) и ниже точка означает дифференцирование по времени.
При составлении ( 1 ) рассматривался случай подключения биморфной пластины к измерительному прибору с большим входным сопротивлением ( электрический холостой ход ), а также учитывалось противоположное направление вектора аксиальной поляризации в двух используемых пьезокерамических элементах.
В этом случае нормальная компонента вектора напряженности  определяется  из условия отсутствия тока смещения на лицевых электродах  , т.е.

,      

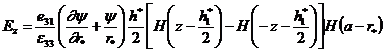а  изгибающие моменты и поперечная сила  с учетом кинематических гипотез для тонких пластин:

    Система дифференциальных уравнений ( 1 ) включает в себя ступенчато-переменные коэффициенты , поэтому  являются непрерывными кусочно-гладкими функциями. При этом точка  является особой, в которой наблюдается резкое изменение, в виде скачка, градиента  изгибающих моментов и поперечной силы (нормальных и касательных напряжений). Данная особенность учитывается с помощью функций
Потенциал электрического поля  , генерируемый в пьезокерамических пластинах, определяется в результате интегрирования равенства ( 4 ), принимая во внимание заземление металлической подложки, а электрическое напряжение холостого хода  вычисляется по формуле

                      

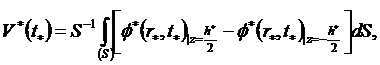
где   площадь пьезокерамической пластины.
В результате имеем следующее выражение для функции :

      3. Построение общего решения.

Начально-краевую задачу ( 1 ) – ( 3 ) относительно функций   решаем, используя  структурный  алгоритм  метода конечных интегральных преобразований КИП [ 7 ]  . Введем  на  сегменте  [ 0,1 ]   КИП  с  неизвестными  компонентами    вектор-функции  ядра  преобразования  и  весовыми  функциями 

где положительные параметры образующие счетное  множество
Равенство  ( 7 ) представляет  трансформанту, а  ( 8 )  формулы  обращения  метода  КИП.
При  этом  круговые  частоты  осесимметричных  колебаний биморфной пластины   связаны  с   зависимостью

                                                                    

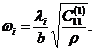
Принимая во внимание кусочно-гладкий характер функций , и представляя  их в виде

подвергаем  систему  уравнений ( 1 ) и начальные условия ( 3 )  преобразованиям КИП в  соответствии  со структурным  алгоритмом [ 7 ].
В результате  получаем  счетное  множество  задач  Коши  для трансформанты

и, с учетом ( 2 ),  однородную  краевую  задачу  для  компонент  ядра  КИП

      В соотношениях ( 10 ) – ( 14 ) приняты следующие обозначения

                     ,
 ,

     

 ,

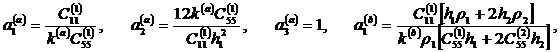
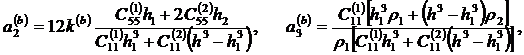
     Равенства ( 14 ) являются условиями неразрывности деформаций и усилий в точке , которые удовлетворяются при выполнении условия

                             ,
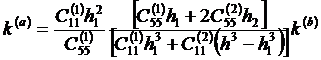коэффициент поперечного сдвига биморфной пластины на участке .
Кроме того, при   определении   ( 10 ) - ( 14 )  использовалось  условие инвариантности ( 1 ) и ( 12 ),   позволившие определить весовые функции

                                                                                                

Решение  уравнения  ( 10 ) при  условиях  ( 11 )  записывается  в  виде:

     Система  ( 12 ) приводится к однородному дифференциальному уравнению четвертого порядка относительно функции , которое допускает факторизацию на коммутативные сомножители второго порядка и может представлено в виде :

      Общий интеграл равенства ( 16 ) имеет вид

     Здесь    ,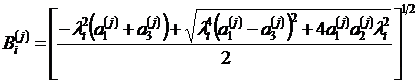
 постоянные интегрирования,  обыкновенные и модифицированные функции

Бесселя первого и второго родов порядка .
Используя зависимости между  и , полученные в процессе приведения  ( 12 ) к ( 16 ),  получаем  выражения для  второй  компоненты  ядра преобразований:

     Подстановка ( 17 ), ( 18 ) в ( 13 ), ( 14 )  позволяет сформулировать трансцендентное уравнение для определения и выражения для постоянных интегрирования .
Применяя  к  трансформанте  ( 15 ) формулы  обращения  ( 8 )  получаем, с учетом (17), (18)  выражения  для  
4. Численные результаты. В качестве примера рассматривается  биморфная пластина (  мм,  мм ,  мм, мм ), имеющая следующие физические характеристики материала  стальной подложки и аксиально поляризованной пьезокерамической пластины состава РХЕ-5 : H/м,
кг/м,  H/м, кг/м.
Расчеты приводятся для случая действия равномерно распределенной гармонической нагрузки:
, где  ,  - частота  и амплитудное значение.
На рис.2,3 показаны графики изменения вертикальных перемещений центра пластины  во  времени  при  различных  частотных  характеристиках  внешнего воздействия. Сплошной линией обозначены результаты, полученные на основании построенного в настоящей работе алгоритма, а пунктирной – осциллограммы, построенные без учета функций .
Отмечаем, что  увеличение частоты внешнего воздействия в рассматриваемом диапазоне приводит к росту перемещений, т.е. более полному проявлению инерционных свойств рассматриваемой системы.
Кроме того, учет особенностей в точке с помощью функций  приводит к «ужесточению» рассматриваемой системы и уменьшению перемещений.    
Эффективность электромеханического преобразования энергии биморфных пластин оценивается с помощью динамического коэффициента электромеханической связи  , который, как правило, представляет отношение резонансных частот вычисляемых для различных электрических краевых условий на электродном покрытии [ 8 ]. Расчетные соотношения, построенные в настоящей работе, позволяют определить меру преобразования энергии с помощью более очевидной характеристики, а именно вертикальных перемещений пьэзоэлемента, которые определяются трансформантой нагрузки . В этом случае зависимость  коэффициента  от  радиуса пьезокерамических пластин вычисляется по формуле:

    Рис.2. - Изменение вертикальных перемещений   во  времени  при  
(-  собственные значения первой резонансной частоты )

   Рис.3. - Изменение вертикальных перемещений   во  времени  при

                                                      .
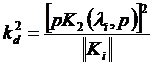На рис.4 представлены графики изменения  для первых двух мод собственных колебаний жестко закрепленного биморфа. Сплошная и пунктирная кривые соответствуют первому и второму номеру частот. Результаты расчета показывают, что если основной вклад в напряженно-деформированное состояние пластины вносит первая частота собственных колебаний, то оптимальное отношение радиусов подложки и пьезопластины  равно 0.68. В случае, когда  определяющей характеристикой является вторая частота, то данное отношение равно 0.43 или 0.86.

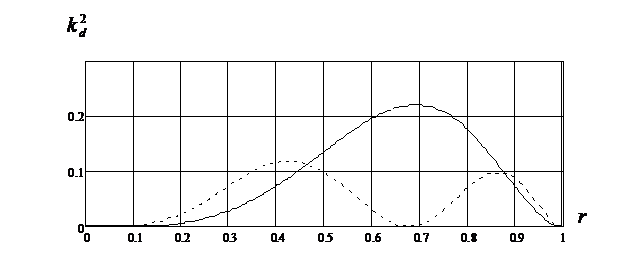
 Рис.4. - Зависимость динамического коэффициента электромеханической связи от радиуса  пьезокерамических пластин

      В заключении отмечаем, что построенный алгоритм решения можно использовать также и при решении задач обратного пьэзоэффекта. Для этого необходимо провести соответствующую замену правых частей дифференциальных уравнений ( 1 ).

   Литература:

1.Евсейчик, Ю.Б. Чувствительность биморфного преобразователя типа металл-пьезокерамика [Текст] // Прикл. мех., 1990.- 26.- №12.- С. 67-75.
2.Евсейчик, Ю.Б., Медведев К.В. Чувствительность гидроакустического датчика давления [Текст] // Гидравлика и гидротехника. Науч.- техн. сб. –Киев: НТУ, 2008. –Вып.62. –С.10-16.
3.Рудницкий, С.Н. Шарапов В.М., Шульга Н.А.    Колебания дискового биморфного преобразователя типа металл–пьезокерамика [Текст]// Прикл. мех.1990.–26. - №10. –С. 64–72.
4.Тимошенко С.П. Пластины и оболочки [Текст]/ С.П. Тимошенко, С. Войновский-Кригер. –М.: Наука, 1966. – 625 с.
5.Гельфанд, И.М. Обобщенные функции и действия над ними [Текст] / И.М. Гельфанд, Г.Е. Шилов. –М.: Физматгиз., 1959. – 470 с.
6.Хмелев, В.Н., Галахов А.Н., Лебедев А.Н., Шалунов А.В., Шалунова К.В. Исследование зависимости геометрических размеров на характеристики излучателя в виде пластины [Текст] // Мат-лы  Всероссийск. конф. ИАМП-2010. г.Бийск, 2010. –С.200-206.
7.Сеницкий,  Ю.Э. Многокомпонентное  обобщенное  конечное  интегральное  преобразование  и  его  приложение  к  нестационарным  задачам  механики [Текст] // Изв. вузов. Математика, 1991. - №4. - С. 57-63.
8. Ватульян, А.О., Рынкова А.А. Об одной модели изгибных колебаний пьезоэлектрических биморфов с разрезными электродами и ее приложение [Текст] // Изв. РАН. МТТ. 2007. -№4. – С.114-122.