Методы скелетной анимации для трансформации полигональных поверхностей трёхмерных моделей

Аннотация

А.А. Букатов, Е.Е. Гридчина, Д.А. Заставной

  В статье показано развитие методов реалистичной деформации трёхмерных моделей на основе скелетной анимации. Подробно описывается распространённый алгоритм Linear Blend Skinning, анализируются его недостатки. Рассматриваются новейшие методы скелетной анимации, основанные на трансформации оболочки модели, выявляются дальнейшие возможные пути развития отрасли.

Ключевые слова: скелетная анимация, скиннинг

05.13.11 - Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей

1. ВВЕДЕНИЕ
Одним из основных этапов при разработке 3D-видеоигр и мультипликационных фильмов является собственно анимация трёхмерных моделей. Трёхмерная модель обычно является полигональной трёхмерной поверхностью, анимация которой в конечном этапе сводится к трансформациям (перемещениям) вершин, образующих эту поверхность. Анимация моделей может задаваться  различными способами, включая методы Motion Capture, моделирования физического поведения объектов, анатомии реального человека и т.д. Наибольшее распространение, однако, получили методы скелетной анимации.
В данной статье описываются основы скелетной анимации в традиционном виде и недостатки, возникающие при его практическом применении. Кроме того, приводится анализ работ, развивающих принципы скелетной анимации, в том числе, для устранения этих недостатков.

2. ТЕРМИНОЛОГИЯ
В данной статье под моделью персонажа понимается трёхмерная полигональная сетка (polygon mesh) или оболочка, которая представляет собой совокупность вершин, рёбер и граней, определяющих форму отображаемого полигонального объекта. С вершиной связана информация о её координатах, векторах нормали и координатах налагаемых текстур – растровых изображений, используемых  для задания цвета, иллюзии рельефа и детализации модели.
Термин «базовая форма» используется для описания недеформированной модели персонажа. Базовое положение вершины – положение вершины в базовой форме модели. Под ключевой формой подразумевается форма, которая придаётся модели в ключевом кадре анимации. Под анимацией понимается трансформация оболочки модели из начального положения в конечное (из одной ключевой формы в другую). Форма модели в каждом промежуточном кадре интерполируется по ключевым формам. При этом может применяться дискретная, линейная или нелинейная интерполяция (например, кривые Безье).

3. МОРФИНГ
Алгоритм морфинга (morphing), также известный как  shape interpolation и shape blending, является одним из базовых методов анимации и составляет конкуренцию методам скелетной анимации в таких областях, как лицевая анимация. Морфинг предполагает создание ключевых форм модели, для каждой из которых положение всех вершин полигональной сетки задается в режиме скульптурной лепки. Важным условием для применения морфинга является совпадение топологии базовой формы модели и всех ключевых форм (одинаковое количество вершин). Трансформированное положение отдельной вершины  относительно двух ключевых форм рассчитывается по формуле:
,
где  – положение вершины в i-ой ключевой форме; φ_i – степень вклада i-ой формы в трансформированное положение вершины,φ_i∈[0,1].
Концепция морфинга была описана в работе Бергерона [1]. Интерполяция форм применялась как для анимации лица, так и для анимации движений персонажа в целом. Сегодня морфинг является популярным инструментом для лицевой анимации и даёт полный контроль над деформациями всей модели, но требует создания большого количества ключевых форм для синтеза реалистичных деформаций, что делает его очень трудозатратным с точки зрения работы аниматора.  Кроме того, морфинг чувствителен к замене анимируемой модели: перенос результатов работы над одной моделью на другие модели практически не возможен (частично это допустимо только при полном совпадении топологии). На практике линейность интерполяции усложняет работу аниматора, так как приходится задавать ключевые формы через каждые три-пять кадров анимации [2], чтобы достигнуть визуально приятного результата.

4. БАЗОВЫЕ МЕТОДЫ СКЕЛЕТНОЙ АНИМАЦИИ
4.1. Понятие скелетной анимации

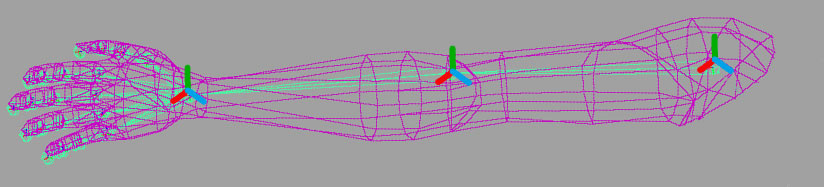
Рис. 1. Полигональная модель руки.

Методы скелетной анимации основаны на использовании скелета, представляющего собой, как правило, иерархическую структуру костей. С каждым узлом структуры связаны своя локальная система координат (см. рис. 1) и трёхмерное преобразование. Трёхмерное преобразование может быть описано матрицей 4´4, различные компоненты которой соответствуют операциям вращения, перемещения и масштабирования соответственно. Каждая кость занимает свое место в иерархии скелета и подвергается влиянию других костей: каждая дочерняя кость наследует трансформации родительской кости. Расположение узлов скелета, соответствующее базовой форме модели, называется позой привязки (binding pose).
Для позы привязки матрица преобразования B_i i-ого сустава скелета будет рассчитываться по следующей формуле:
,
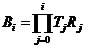где T_j– матрица смещения j-ого сустава; R_j – матрица вращения j-ого сустава;  сустав с индексом j=0 является корневым, а сустав с индексом  j является родительским по отношению к суставу с индексом j+1, j= .
Для любой позы, отличной от позы привязки, матрица преобразования сустава будет вычисляться аналогичным образом. Описанный способ преобразования положения узлов скелета именуется прямой кинематикой. В случае использования обратной кинематики аниматор в интерактивном режиме задаёт для руки или ноги модели нужное положение, а программа автоматически вычисляет для каждого из суставов соответствующие углы с учётом таких ограничений, например, как фиксированные размеры.
Каждой вершине модели ставится в соответствие определённая кость скелета. Этот процесс называется привязкой (binding). Привязка вершины может производиться автоматически к ближайшей кости или  осуществляться более тонко – путём задания связей вручную. Таким образом, при трансформации положения отдельной кости изменяется положение связанных с ней вершин. Благодаря этому работа аниматора значительно упрощается: отпадает необходимость анимировать каждую вершину отдельно, так как вершина наследует трансформации кости, с которой она связана.
Первичный вариант алгоритма скелетной анимации был предложен Э. Катмулом в 1972 году [3]. Описывая проблемы автоматизированной анимации в более поздней статье  [4], Э. Катмул  упоминает также об алгоритме двухмерной скелетной анимации Н. Буртника и М. Вейна [5], предложенного в 1976 году. 

4.2. Сегментная анимация
Одним из представлений модели персонажа в трёхмерной графике является иерархия сегментов, которые представляют собой недеформируемые поверхности [6]; это означает, что все вершины сегмента при анимации трансформируются одинаково. Иерархия сегментов являлась прообразом для иерархии скелета  в последующих методах. Для анимации сегментных моделей достаточно хранить для каждого сегмента информацию о положении вершин сегмента, центра сегмента  и  матрицу преобразования.  Ввиду простоты этот метод активно применялся в ранних видоеиграх. Главным недостатком метода является то, что результаты его работы не выглядят реалистично. Это вызвано, в том числе, и неизбежными разрывами в местах сочленений недеформируемых тел иерархии при анимации.

4.3. Скелетная анимация без весов
Алгоритм анимации с привязкой вершины к одной кости (stitching, rigid skinning, basic skeletal animation) подробно описан в [7] и использует модель персонажа, представленную единой оболочкой, а не иерархией отдельных сегментов.   Данный метод получил название stitching (букв. «сшивание»), так как к кости привязывается не поверхность или сегмент целиком, а каждая из вершин.
Трансформированное положение отдельной вершины  рассчитывается по формуле:     , где  – базовое положение вершины;  B – матрица сустава, трансформации которого наследует рассматриваемая вершина,  в позе привязки; W – текущая матрица данного сустава, соответствующая трансформированной позе скелета. Все компоненты формулы заданы в глобальных координатах. Данной формуле можно дать геометрическую интерпретацию (см. рис. 2).

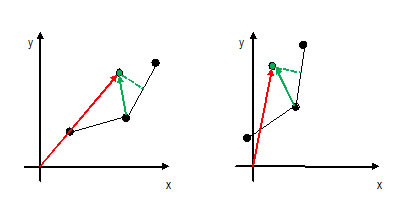
Рис. 2. Инвариантность положения вершины относительно системы координат, связанной с суставом.

Сначала осуществляется перевод координат вершины из глобальной системы координат в локальную систему координат, которая связана с рассматриваемым суставом. При перемещении самого сустава положение вершины в системе координат сустава  остаётся неизменным. Затем производится расчёт трансформированного положения сустава – вычисляется матрица W. После этого осуществляется обратный переход в глобальную систему координат: вершина наследует трансформации сустава, и итоговое положение вершины вычисляется как .
При такой привязке неизбежны растяжения и самопересечения модели, на сгибах модель выглядит неестественно (см. рис. 3).

Рис. 3. Скелетная анимация без весов. Жёсткая привязка полигональной сетки к скелету.

4.4. Скелетная анимация с весами. Linear blend skinning (LBS)
Следующим шагом в развитии алгоритмов скининга является скелетная анимация с весовыми коэффициентами. Впервые данная концепция была представлена в работах [8, 9], рассматривающих движение кисти руки. Данный алгоритм известен под несколькими названиями: linear blend skinning (LBS),  vertex blending, smooth skinning, enveloping, matrix palette skinning, Subspace-Skeletal Deformations (SSD) (для обозначения данного подхода далее будем использовать аббревиатуру LBS). Несмотря на то, что алгоритм начал широко применяться довольно рано, основные принципы алгоритма в литературе были изложены только в конце 1990-х годов [10, 11].
LBS допускает влияние на вершину не одной, а нескольких костей. Для каждой кости определяется свой вес, то есть степень влияния данной кости на перемещения вершины. Чем больше вес определённой кости, тем сильнее вершина смещается под её влиянием. Задание и корректировка весовых коэффициентов является трудоёмким аспектом данного алгоритма на практике, так как требует охвата всего диапазона движений персонажа и учёта перекрёстных связей между весами различных суставов [12]. Трансформированное положение отдельной вершины  рассчитывается по формуле:
, ,                                                           (1)
где w_i – вес i-ой кости.
Важно отметить, что LBS остаётся общепринятой технологией скининга [15, 16, 17]. Востребованность LBS отмечают  профессионалы в сфере производства визуальных эффектов, анимационных фильмов и видеоигр [18].  Отметим достоинства и недостатки LBS.

Достоинства LBS:

• Переносимость анимации на другие модели с аналогичной топологией скелета.
• Простота расчётов и высокая вычислительная эффективность.
• Простота аппаратной реализации алгоритма [19].

Недостатки LBS:

1. Отсутствие реалистичности, симуляции мышц, деформации кожи.
2. Необходимость продумывания и создания иерархии скелета для модели.
3. Трудоёмкость корректировки весов.

Для упрощения работы c LBS были разработаны определённые вспомогательные инструменты, которые позволяют проводить автоматическое построение скелета по модели персонажа [20, 21, 22, 23]. Кроме того, для удобства работы с весами были созданы виртуальный аэрограф, позволяющий работать с весами опосредовано, через изображение, а также алгоритмы автоматического распределения весов [22, 24].
Основной недостаток LBS заключается в отсутствии реалистичности получаемых изображений. Артефакты LBS (например, [2, 13]) указывают на недостаточную гибкость алгоритма. Особенно яркие примеры артефактов LBS связанны с отработкой сгибов руки в локте. Данные артефакты вызваны тем, что кости и суставы в скелетной анимации не моделируются как протяженные объекты, сустав представляет собой математическую абстракцию – точку, вокруг которой производится вращение части тела [14].
Типичные искажения LBS в области локтя при сгибе принято называть collapsing elbow (букв. «сплющивающийся локоть») (см. рис. 4).

Рис. 4. Сплющивание в области локтя (LBS).

Важно заметить, что потеря объёма характерна для данного метода при анимации всех сочленений данного типа, в особенности плеча. Артефакт, связанный с вращением сустава на 180°, получил  название candy wrapper (букв. «конфетная обёртка»). Рассмотрим, что является причиной данного артефакта. Пусть вершина  находится  в области сочленения двух костей i и j и в равной степени испытывает их влияние (w_i = w_j =0.5), где i – родительская кость, а j– дочерняя; и пусть (0, y, 0) –  её положение в локальной системе координат, связанной с костью j. При повороте дочерней кости на 180° вокруг оси Ox трансформированное положение вершины = w_i(0, y, 0)+w_j(0, -y, 0)=(0,0,0), то есть,  все вершины, испытывающие в равной степени влияние обеих костей,  стягиваются в одну точку (см. рис. 5).

Рис. 5. Поворот локтевого сустава на 180˚ (LBS), эффект «конфетной обёртки».

Данные дефекты могут устраняться при помощи средств традиционного алгоритма LBS, в том числе, при помощи введения дополнительных костей, корректирующих аномально трансформирующиеся части поверхностей. Однако это приводит к существенному увеличению количества костей и усложнению скелета, равно как и усложняет процедуру привязки поверхности к костям, что на практике делает анимацию подобных моделей сложной и малоиспользуемой. В предельном случае привязка каждой вершины к отдельно анимируемой кости, конечно же, способна устранить любые дефекты LBS.
Преодолеть данные недостатки призваны новые методы скелетной анимации.

5. ДОПОЛНИТЕЛЬНЫЕ МЕТОДЫ СКЕЛЕТНОЙ АНИМАЦИИ
5.1 Алгоритмы скелетной анимации с использованием эталонных форм
Алгоритмы рассматриваемой группы используют  набор  эталонных форм-примеров моделей и соответствующие им конфигурации скелета. Данные эталонные формы могут быть получены из целого ряда источников: они могут быть сделаны вручную специалистом по 3D-моделированию, являться результатом 3D-сканирования (технология Motion Capture), а также могут быть сгенерированы путём применения алгоритмов, симулирующих анатомию человека. Далее результаты трансформации, полученные с помощью алгоритма LBS, сравниваются с заданными эталонными формами и корректируются в соответствии с ними. Основной недостаток этой группы алгоритмов заключается в необходимости получения и использования очень большого количества эталонных форм для получения реалистичных результатов. Для корректной работы методов необходимо предоставлять такой набор эталонных форм, который будет довольно полно описывать все возможные движения персонажа, то есть будет репрезентативным. Проводя коррекцию работы алгоритма  LBS, данные методы уступают ему в быстродействии.

5.1.1 Pose Space Deformation
Алгоритм анимации в пространстве поз (PSD – Pose Space Deformation) [2] является базовым алгоритмом рассматриваемой группы и сочетает в себе алгоритмы морфинга и скелетной анимации LBS. Данный метод подразумевает использование пар <эталонная форма модели, конфигурация скелета> для подгонки результатов применения LBS к ожидаемой конечной форме. Для синтеза анимации между ключевыми кадрами используется линейная интерполяция с использованием радиальных базисных функций (РБФ). Под РБФ подразумеваются такие вещественные функции, которые зависят от расстояния текущей точки x до центра РБФ c: φ(x,c)= φ( ).
Вершина из исходного положения  перемещается с помощью алгоритма скелетной анимации LBS в положение , i=0,1,…,N. Затем полученная форма компенсируется сдвигами , i=0,1,…,N, которые соответствуют эталонными формам модели x_i,i=0,1,…,N. Таким образом, вершина  в итоге перемещается в положение   . Далее, чтобы получить промежуточные положения вершины, проводится интерполяция по : , где x – промежуточная форма модели, то есть форма отличная от эталонных форм модели;  – евклидово расстояние между формами модели x_i и x_j; φ(x) – гауссова РБФ; w_i – веса соответствующих эталонных форм.
 В силу линейности интерполяции деформации модели в промежуточных кадрах не отвечают в полной мере соответствующим движениям реального человека. Поэтому интерполяцию приходится проводить по большому количеству довольно близких эталонных форм.
Метод анимации в пространстве поз в настоящее время широко применяется, хотя аниматоры  и отмечают определённую сложность работы с PSD: применение данной технологии при моделировании главного персонажа полнометражного анимационного фильма “Bolt”  заняло примерно 3 недели [25]. Чтобы упростить и, соответственно, ускорить работу с PSD, работники Walt Disney Animation Studios были вынуждены разработать большое количество вспомогательных инструментов. В 2006 году была реализована аппаратная визуализация на основе алгоритма PSD [26].
5.1.2 Алгоритм П. Слоана (Shape by Example)
Алгоритм «Shape by Example» (букв. «форма по примеру», далее SE) [27] в отличие от PSD требует решить по одной линейной системе на каждую эталонную форму, а не на каждый компонент вершины (то есть, 3n линейных систем, где n – количество вершин модели). Такая формулировка задачи, как правило, позволяет добиться работы со значительно меньшим объёмом данных. Рассматриваемый алгоритм также использует РБФ при интерполяции, но в комбинации с линейной гиперплоскостью, что позволяет проводить не только более гладкую интерполяцию, но и экстраполяцию.
5.1.3. Алгоритм, основанный на сканировании
В отличие от PSD и SE метод, предложенный Б. Алленом в работе [28], использует в качестве эталонных форм данные, полученные в результате сканирования. Это позволяет получить довольно реалистичные результаты, но ставит новые задачи: дополнение сканограмм для получения целостной формы, определение конфигурации скелета для каждой эталонной формы, установка взаимооднозначного соответствия между эталонными формами. Для расчёта трансформации костей используются кватернионы [29]. При решении задачи интерполяции между эталонными формами при построении изображения модели в произвольной конфигурации автор отмечает недостатки использования РБФ: радиальные базисные функции работают эффективно при вращении кости только по одной оси. Кроме того, РБФ интерпретируют компоненты кватерниона как линейно-независимые и допускают отрицательные значения весовых коэффициентов. В связи с этим для решения задачи интерполяции рассматриваемый алгоритм применяет метод k ближайших соседей: выбираются точки k ближайших эталонных форм и им приписываются веса с учётом их удалённости от формы, соответствующей текущей конфигурации скелета. Интересно, что интерполяция проводится отдельно для каждой части тела, и затем осуществляется плавное сопряжение частей.
5.1.4 Метод П. Края (EigenSkin)
Алгоритм EigenSkin [30] предполагает наличие эталонных форм, полученных в результате работы алгоритмов, симулирующих анатомию человека. EigenSkin не требует хранения смещений для всех эталонных форм, как PSD, а применяет метод главных компонент (МГК) для сжатия исходных данных путём построения базиса эталонных форм. Однако МГК применяется не к полю смещений по всей модели, так как это привело бы к большому числу базисных функций. Вместо этого модель разлагается на составные части, которые определяются по влиянию отдельных костей на поле смещений. В итоге, алгоритм получает набор базисов, который и применяется при визуализации. Таким образом, EigenSkin  реализует линейную версию сложных нелинейных алгоритмов.

5.2 Алгоритмы, обобщающие LBS
Алгоритмы, обобщающие традиционный метод LBS, основаны на альтернативной интерпретации  уравнения скелетной анимации (1). Алгоритмы данной группы достигают более точной аппроксимации и гибкости за счёт связывания с каждым узлом скелета не одного, а нескольких весовых коэффициентов. Задача определения множественных весовых коэффициентов не может быть решена присваиванием значений вручную (как в LBS), в связи с чем для расстановки весов используются эталонные формы. Тем не менее, при таком подходе некоторые веса могут остаться недоопределёнными, что может привести к так называемой «избыточной подгонке» (overfitting). Это возможно, если эталонные формы, соответствующие движению сустава, лежат, например, в одной плоскости.
Хранение большего количества весов приводит к увеличению времени вычислений, а также к необходимости хранения большего по сравнению с LBS количества параметров.

5.2.1 Multi-Weight Enveloping (MWE)
Алгоритм MWE [31] подразумевает подстановку матрицы преобразования  M_i=  в уравнение скелетной анимации (1): . Далее весовые коэффициенты w_i вносятся в матрицу преобразования M_i, давая, таким образом, «весовую матрицу» и увеличивая количество весовых коэффициентов до двенадцати:

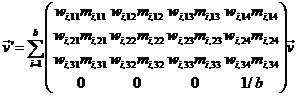
Дополнительные веса позволяют рассчитывать влияние на каждый компонент вершины независимым образом по каждому из компонентов движения кости. Это повышает гибкость алгоритма, что позволяет сократить артефакты LBS. Что касается времени вычислений, то, с одной стороны, MWE требует на одну операцию скалярного умножения меньше, чем LBS; но, с другой стороны, MWE требуется дополнительное время для передачи большего количества параметров. В итоге, сравниваемые методы демонстрируют сходные результаты по времени вычисления [32].  Тем не менее, преимущество гибкости достигается за счёт необходимости задания не одного весового коэффициента, а двенадцати, что затрудняет настройку модели аниматором.

5.2.2. Animation Space
В работе Б. Мерри [33] производится подстановка p_i = w_i   в уравнение скелетной анимации (1): . Таким образом, количество весов, связанных с одной вершиной возрастает до четырёх, что соответствует четырём компонентам вектора  p_i=(x,y,z,0). Это позволяет независимым образом распределять влияние костей на различные координаты вершин, что, в итоге, позволяет сгладить артефакты LBS. Кроме того, уравнение Animation Space является линейным.
Интересно отметить, что, несмотря на использование большего количества параметров, время, необходимое для вычисления нового положения вершины алгоритмом Animation Space, сравнимо со временем LBS [33]. Это объясняется тем, что, во-первых, отпадает необходимость хранить информацию о положении вершин в позе привязки, и, во-вторых, веса рассчитываются заранее, и, таким образом, вычисление нового положения вершины при использовании Animation Space требует на одну операцию скалярного умножения меньше, чем LBS, как и MWE.
Алгоритм MWE в сравнении с Animation Space демонстрирует большую гибкость. Но чем больше дополнительных весов используется, тем больше вероятность того, что некоторые из них будут недоопределены. А это в свою очередь приводит к артефактам, связанным с «избыточной подгонкой».

5.3 Алгоритмы, использующие введение дополнительных костей
Алгоритмы данной группы основываются на добавлении костей в уже существующий скелет с целью добиться большей гибкости при вращении в областях сочленения костей.  Такие дополнительные кости называют псевдокостями. После добавления костей необходимо заново выполнять расстановку весов, что является существенным недостатком данной группы методов скелетной анимации. Кроме того, результаты работы не переносятся на другие модели. С другой стороны, увеличение количества костей может стать причиной невозможности аппаратной визуализации, так как количество данных, связанных с вершиной, которые можно передавать в подпрограмму для обработки на графическом процессоре (шейдер), ограничено. Основным преимуществом рассматриваемой группы алгоритмов является отсутствие необходимости внесения изменений в используемую систему расчёта скелетной анимации.
5.3.1 Алгоритм Дж. Вебера
Дж. Вебер первым в своей работе [13] предложил использовать дополнительные кости около сочленений уже существующих костей – в местах образования артефактов LBS.  Он заметил, что LBS работает корректно при углах до 60 градусов между костями, дополнительные кости позволяют не допустить превышения этого предела.
5.3.2  Алгоритм А. Мора и М. Глейчера
Алгоритм А. Мора и М. Глейчера  [34] интересен тем, что использует псевдокости не только для сглаживания артефактов при вращении, но и для имитации увеличения в объёме мышц при их сокращении с помощью масштабирования дополнительных костей.
5.3.3 Автоматическая линеаризация нелинейных алгоритмов скининга
В работе Л. Кавана [35] развиваются идеи А. Мора и М. Глейчера  [34]. Метод допускает использование произвольного количества псевдокостей и использует эталонные формы, полученные в результате работы симуляционных методов скининга, для их автоматической расстановки.

5.4 Нелинейные алгоритмы
Нелинейные алгоритмы рассматривают  уравнение скелетной анимации (1) не как сопряжение положения вершин, а как комбинацию вращений узлов. Таким образом, происходит расчёт интерполяции вращений суставов. Но, как правило, более продвинутые методы интерполяции предполагают, во-первых, использование более мощных вычислительных ресурсов, а, во-вторых, существенные преобразования графического конвейера приложений. Одной из первых альтернатив линейной интерполяции стала нормированная линейная интерполяция, которая сохраняла длину кости при вычислении промежуточных положений, но не сохраняла постоянную скорость вращения кости. Важно отметить, что данные методы реализуют только трёхмерные преобразования вращения и смещения, как следствие, при масштабировании элементов модели проявляются артефакты.
5.4.1 Bones Blending
Один из первых алгоритмов данной группы [36] использует так называемую сферическую линейную интерполяцию вращений (SLERP), представленную в [37]. Она представляет собой ту же линейную интерполяцию, но проецированную на поверхность единичной сферы. Недостаток использования SLERP состоит в том, что данный алгоритм интерполяции применим только при условии, что на перемещение вершины влияет не более двух костей. Кроме того, алгоритм Bones Blending требует выставления некоторых параметров интерполяции пользователем.
5.4.2 Spherical Blend Skinning (SBS)
В методе [38] развиваются идеи сферической линейной интерполяции SLERP и [36]. Для параметризации преобразований костей используются кватернионы. Для сопряжения более двух кватернионов (то есть, для преодоления ограничений SLERP) используется линейное вычисление среднего по нескольким кватернионам. Данный подход назван линейной интерполяцией кватернионов (QLERP). Использование QLERP не эквивалентно использованию SLERP, а лишь является аппроксимацией результатов SLERP. В работе также решается задача выбора центра вращения. Отмечается, что SBS даёт более грубые результаты по сравнению с SLERP и может вычислять только вращения, но стоимость вычисления сокращается. При оптимизации используется разложение по сингулярным числам матрицы (SVD). Также был предложен вариант реализации SBS на GPU [39].
5.4.3 Скининг с использованием бикватернионов
В работе [40] предлагается использование двойных кватернионов, которые в отличие от обычных кватернионов могут описывать как вращения, так и перемещения одновременно. С помощью бикватернионов конструируются аналоги методов, которые вычисляли исключительно вращение, таких как [37, 39]. В результате численных экспериментов подтверждается, что метод линейного сопряжения двойных кватернионов DLB (Dual Quaternion Linear Blending) является наиболее эффективным по сравнению с Log и SBS, но немного проигрывает в скорости LBS. Тем не менее, использование бикватернионов требует передачи лишь 8 параметров, а не 12 как в LBS, что довольно значимо при аппаратной реализации алгоритмов. С одной стороны, DLB не демонстрирует артефактов  LBS, но, с другой стороны, имеет свои недостатки, противоположные недостаткам LBS: алгоритм всегда выбирает кратчайший путь, и иногда могут появиться нежелательные выпячивания в области колена, локтя, подмышки [41].
Из всех представленных решений  скининг с использованием двойных кватернионов (наряду с PSD) можно считать наиболее популярным, так как данный алгоритм был реализован в версии 2011 года графического 3D редактора Maya, кроме того, метод, аппроксимирующий DLB, [42] использовался в игровой индустрии [43].

6. ЗАКЛЮЧЕНИЕ
Методы традиционной скелетной анимации LBS является основным и универсальным методом, широко применяющимся на практике. Присущие ему недостатки – артефакты – могут быть частично компенсированы при помощи усложнения скелета, что, однако, приводит к серьезным трудностям при практическом применении, в том числе, при задании весов костей. Реальной и весьма эффективной альтернативной является технология PSD, которая удачно сочетает задание анимации модели при помощи традиционной LBS и блендинга; этот метод широко используется в настоящее время, но так же является весьма трудоёмким.
Предложенные в литературе методы обладают некоторыми недостатками, среди которых следует отметить следующие. Во-первых, эти методы ориентированы, в первую очередь, на устранение артефактов, возникающих при вращении костей, тогда как PSD позволяет учитывать, например, изменение рельефа мышц.  Далее, некоторые предложенные в литературе идеи, например, разделение весов для разных трансформаций, трудно применить на практике. Наконец, опубликованные материалы не позволяют однозначно определить, насколько применение этих методов будет способствовать устранению дефектов скелетной анимации, и в какой степени эти методы возможно сочетать с LBS, остающейся базовым средством анимации моделей. Очевидно, что представляется перспективным дальнейшее развитие методов скелетной анимации, с учетом более тесной интеграции с практически используемыми технологиями.

ЛИТЕРАТУРА
1. Bergeron, P. Controlling facial expressions and body movements in the computer-generated animated short ’Tony De Peltrie’ / P. Bergeron, P. Lachapelle // SIGGRAPH ’85: ACM SIGGRAPH Tutorial Notes.— New York, NY, USA: ACM, 1985.
2. Lewis, J. P. Pose space deformation: a unified approach to shape interpolation and skeleton driven deformation / J. P. Lewis, M. Cordner, N. Fong // Proceedings of the 27th annual conference on Computer graphics and interactive techniques.— SIGGRAPH ’00.—New York, NY, USA: ACM Press/Addison-Wesley Publishing Co., 2000.— Pp. 165–172.
3. Catmull, E. E. A system for computer generated movies / E. E. Catmull // Proc. ACM Annual Conf.— 1972.—August.— Pp. 422–431.
4. Catmull, E. The problems of computer-assisted animation / E. Catmull // Proceedings of the 5th annual conference on Computer graphics and interactive techniques.— SIGGRAPH ’78.— New York, NY, USA: ACM, 1978.— Pp. 348–353.
5. Burtnyk, N. Interactive skeleton techniques for enhancing motion dynamics in key frame animation / N. Burtnyk, M. Wein // Communications of the ACM.— 1976.—October.— Vol. 19.— Pp. 564–569.
6. Lander, J. On Creating Cool Real-Time 3D.— http://www.gamasutra.com.— 1997.—October.
7. Woodland, R. Filling the Gaps — Advanced Animation Using Stitching and Skinning / R. Woodland // Best of Game Programming Gems / Ed. by M. DeLoura.— Boston, MA, USA: Course Technology, Cengage Learning, 2008.— 549 pp.
8. Magnenat-Thalmann, N. Joint-dependent local deformations for hand animation and object grasping / N. Magnenat-Thalmann, R. Laperri`ere, D. Thalmann // Proceedings on Graphics interface ’88.— Toronto, Ont., Canada, Canada: Canadian Information Processing Society, 1988.— Pp. 26–33.
9. Magnenat-Thalmann, N. Making them move / N. Magnenat-Thalmann, D. Thalmann / Ed. by N. I. Badler, B. A. Barsky, D. Zeltzer.— San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 1991.— Pp. 243–262.
10. Lander, J. Skin them bones: Game programming for the web generation / J. Lander // Game Developer Magazine.— 1998.—May.— Pp. 11–16.
11. Lander, J. Over my dead, polygonal body / J. Lander // Game Developer Magazine.— 1999.— October.— Pp. 17–22.
12. Освоение Maya 8.5 / Д. Кундерт-Гиббс, М. Ларкинс, Д. Деракшани, Э. Кунзендорф.— Москва: ООО .И.Д. Вильямс., 2007.— 928 с.
13. Weber, J. Run-time skin deformation / J. Weber // Proceedings of Game Developers Conference.— 2000.
14. Herbez, A. Rigging for Animation 1 - Skeletons and Skinning, Maya Online – Additional Resources. Электронная версия: http://www.purplestatic.com/courses/maya/431/06/index.htm.
15. Example-based dynamic skinning in real time / X. Shi, K. Zhou, Y. Tong et al. // ACM SIGGRAPH 2008 papers.— SIGGRAPH ’08.— New York, NY, USA: ACM, 2008.— Pp. 29:1– 29:8.
16. Landreneau, E. Simplification of Articulated Meshes / E. Landreneau, S. Schaefer // Comput. Graph. Forum.— 2009.— Vol. 28, no. 2.— Pp. 347–353.
17. Vasilakis, A. A. GPU rigid skinning based on a refined skeletonization method / A. A. Vasilakis, I. Fudos // Comput. Animat. Virtual Worlds.— 2011.—January.— Vol. 22.— Pp. 27–46.
18. McLaughlin, T. Character rigging, deformations, and simulations in film and game production / T. McLaughlin, L. Cutler, D. Coleman // ACM SIGGRAPH 2011 Courses.— SIGGRAPH’11.— New York, NY, USA: ACM, 2011.— Pp. 5:1–5:18.
19. Lee, M. Seven ways to skin a mesh: Character skinning revisited for modern gpus. / M. Lee // In Proceedings of GameFest, Microsoft Game Technology Conference. –  2007.
20. Verroust, A. Extracting skeletal curves from 3d scattered data / A. Verroust, F. Lazarus // Shape Modeling and Applications, International Conference on.— 1999.— P. 194.
21. Hagland, T. A Fast and Simple Skinning Technique / T. Hagland // Game Programming Gems / Ed. by M. DeLoura.— Rockland, MA, USA: Charles River Media, 2000.— 614 pp.
22. Baran, I. Automatic rigging and animation of 3D characters / I. Baran, J. Popovic // ACM SIGGRAPH 2007 papers.— SIGGRAPH ’07.— New York, NY, USA: ACM, 2007.
23. Harmonic Skeleton for Realistic Character Animation / G. Aujay, F. Hetroy, F. Lazarus, C. Depraz // ACM-SIGGRAPH/Eurographics Symposium on Computer Animation / edited by D. Metaxas, J. Popovic.— San Diego, United States: ACM, 2007.
24. Wareham, R. Bone glow: An improved method for the assignment of weights for mesh deformation / R. Wareham, J. Lasenby // AMDO 2008 / Ed. by F. J. P. L’opez, R. B. Fisher.— Vol. 5098.— Berlin Heidelberg: Springer-Verlag, 2008.
25. Lee, G. S. Practical experiences with pose space deformation / G. S. Lee, F. Hanner // ACM SIGGRAPH ASIA 2009 Sketches.— SIGGRAPH ASIA ’09.— New York, NY, USA: ACM, 2009.— Pp. 43:1–43:1.
26. Rhee, T. Real-Time Weighted Pose-Space Deformation on the GPU / T. Rhee, J. P. Lewis, U. Neumann // Computer Graphics Forum.— 2006.— Vol. 25, no. 3.— Pp. 439–448.
27. Sloan, P.-P. J. Shape by example / P.-P. J. Sloan, C. F. Rose, III, M. F. Cohen // Proceedings of the 2001 symposium on Interactive 3D graphics.— I3D ’01.— New York, NY, USA: ACM, 2001.— Pp. 135–143.
28. Allen, B. Articulated body deformation from range scan data / B. Allen, B. Curless, Z. Popovic // Proceedings of the 29th annual conference on Computer graphics and interactive techniques.— SIGGRAPH ’02.— New York, NY, USA: ACM, 2002.— Pp. 612–619.
29. Цисарж, В. Математические методы компьютерной графики / В. Цисарж, Р. Марусик.— Киев: Факт, 2004.— 464 с.
30. Kry, P. G. Eigenskin: real time large deformation character skinning in hardware / P. G. Kry, D. L. James, D. K. Pai // Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation.— SCA ’02.— New York, NY, USA: ACM, 2002.— Pp. 153–159.
31. Wang, X. C. Multi-weight enveloping: least-squares approximation techniques for skin animation / X. C.Wang, C. Phillips // Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation.— SCA ’02.— New York, NY, USA: ACM, 2002.—Pp. 129–138.
32. A comparison of linear skinning techniques for character animation / D. Jacka, A. Reid, B. Merry, J. Gain // Proceedings of the 5th international conference on Computer graphics, virtual reality, visualisation and interaction in Africa.— AFRIGRAPH ’07.— New York, NY, USA: ACM, 2007.— Pp. 177–186.
33. Merry, B. Animation space: A truly linear framework for character animation / B. Merry, P. Marais, J. Gain // ACM Trans. Graph.— 2006.—October.— Vol. 25.— Pp. 1400–1423.
34. Mohr, A. Building efficient, accurate character skins from examples / A. Mohr, M. Gleicher // ACM SIGGRAPH 2003 Papers.— SIGGRAPH ’03.— New York, NY, USA: ACM, 2003.— Pp. 562–568.
35. Kavan, L. Automatic linearization of nonlinear skinning / L. Kavan, S. Collins, C. O’Sullivan // Proceedings of the 2009 symposium on Interactive 3D graphics and games.— I3D ’09.— NewYork, NY, USA: ACM, 2009.— Pp. 49–56.
36. Kavan, L. Real time skin deformation with bones blending / L. Kavan, J. Zara // WSCG.— 2003.
37. Shoemake, K. Animating rotation with quaternion curves / K. Shoemake // Proceedings of the 12th annual conference on Computer graphics and interactive techniques.— SIGGRAPH ’85.— New York, NY, USA: ACM, 1985.— Pp. 245–254.
38. Kavan, L. Spherical blend skinning: a real-time deformation of articulated models / L. Kavan, J. Zara // Proceedings of the 2005 symposium on Interactive 3D graphics and games.— I3D ’05.— New York, NY, USA: ACM, 2005.— Pp. 9–16.
39. Andersen, K. A. Spherical Blend Skinning on GPU / K. A. Andersen // Memory.— 2007.
40. Skinning with dual quaternions / L. Kavan, S. Collins, J. Zara, C. O’Sullivan // Proceedings of the 2007 symposium on Interactive 3D graphics and games.— I3D ’07.— New York, NY, USA: ACM, 2007.— Pp. 39–46.
41. Maya 2011 Dual quaternion skinning. – [Электронный ресурс] Tech Artists Forums. Режим доступа:  http://tech-artists.org/forum/showthread.php?1176-Maya-2011-Dual-quaternion-skinning (Дата обращения: 15.04.12)
42. Geometric skinning with approximate dual quaternion blending / L. Kavan, S. Collins, J. Zara, C. O’Sullivan // ACM Trans. Graph.— 2008.—November.— Vol. 27.— Pp. 105:1–105:23.
43. Frey, I. Z. Spherical skinning with dual quaternions and qtangents / I. Z. Frey, I. Herzeg // ACM SIGGRAPH 2011 Talks.— SIGGRAPH ’11.— New York, NY, USA: ACM, 2011.— P. 11.