Моделирование алгоритма краткосрочного прогнозирования изменения быстроизменяющейся физической величины в реальном времени
Аннотация
Предложена модель и алгоритм краткосрочного прогнозирования изменения быстроизменяющейся физической величины, характеризующей состояние технического объекта. Модель основана на использовании сглаживающих временных рядов. Определены особенности настройки и использования модели. Приведенные соотношения и алгоритм краткосрочного прогнозирования ориентированы на выполнение обработки данных в микроконтроллере микропроцессорного модуля в реальном времени. Моделирование показало эффективность предлагаемого подхода к прогнозированию изменения параметров объекта.
Ключевые слова: прогнозирование, алгоритм, временной ряд, сглаживание
05.11.17 - Приборы, системы и изделия медицинского назначения
Введение
Необходимость опережающего мониторинга состояния технического объекта для предотвращения и управления протеканием нештатных ситуаций в целях их ликвидации с минимальными последствиями делает постановку и выполнение задачи определения прогнозируемых значений параметров, а также прогнозируемой оценки состояния отдельных параметров технического объекта или их совокупности в реальном времени актуальной и своевременной. Современное развитие микропроцессорной техники позволяет реализовать эту задачу с использованием микропроцессорных модулей (ММ) в составе информационных систем сложных технических объектов, таких как системы активной безопасности и инерциальной навигации автомобиля. Оценки, реализуемые в ММ, обеспечивают высокую динамику реакции на ситуации. Для выполнения прогнозной оценки значений параметров технического объекта с помощью ММ целесообразно использовать простые модели, позволяющие получить результат в режиме реального времени без существенной нагрузки на микроконтроллер модуля, например, модели, в основе которых лежат методы анализа и прогнозирования временных рядов [1, 2].
В настоящей статье рассмотрены модель и алгоритм прогнозирования значений быстропеременной физической величины на основе использования многократного экспоненциального сглаживания ее временного ряда. Эффективность модели и алгоритма оценивается на основе обработки данных об изменении значений проекций вектора ускорения автомобиля, измеренных с помощью трехосевого акселерометра в реальных условиях движения.
Моделирование процесса прогнозирования изменения параметра технического объекта
При построении алгоритма прогнозирования на основе модели многократного экспоненциального сглаживания временного ряда предполагалось, что шаг дискретизации при съеме данных можно установить небольшим, таким, что изменение параметра в течение нескольких последовательных шагов будет незначительным. Это позволит повысить точность прогнозирования.
Пусть значения контролируемого параметра технического объекта ![]() измеряются микроконтроллерным модулем в дискретные моменты времени с постоянным шагом h. В результате получим массив
измеряются микроконтроллерным модулем в дискретные моменты времени с постоянным шагом h. В результате получим массив ![]() измеренных значений параметра
измеренных значений параметра ![]() в точках
в точках ![]() ;
; ![]() . Необходимо определить значение параметра y в точках
. Необходимо определить значение параметра y в точках ![]() ,
, ![]() , где T – текущее значение времени относительно которого делается прогноз на k - шагов или на промежуток времени
, где T – текущее значение времени относительно которого делается прогноз на k - шагов или на промежуток времени ![]() , называемый временем упреждения [1], а К – число, определяющее диапазон прогнозирования.
, называемый временем упреждения [1], а К – число, определяющее диапазон прогнозирования.
В качестве прогнозирующего ряда использовалась модель сглаживающего временного ряда первой степени вида [1, 3]
![]() , (1)
, (1)
характеризующаяся низкой сложностью и обладающая хорошими адаптивными свойствами.
Тогда прогнозное значение ![]() в точках
в точках ![]() :
:
![]() , (2)
, (2)
где ![]() и
и ![]() – экспоненциальные средние, которые определяются на момент Т по формулам:
– экспоненциальные средние, которые определяются на момент Т по формулам:
![]() ,
, ![]() , (3)
, (3)
![]() – постоянная сглаживания, которую необходимо подбирать,
– постоянная сглаживания, которую необходимо подбирать, ![]() .
.
Для того, чтобы запустить процесс расчета необходимо задать начальные значения ![]() и
и ![]() :
:
![]() ,
, ![]() (4)
(4)
Здесь ![]() и
и ![]() – начальные оценки коэффициентов
– начальные оценки коэффициентов ![]() и
и ![]() в (1).
в (1).
Исследование возможности использования модели адаптивного временного ряда для прогнозирования параметра технического объекта проводилось на основе данных, снимаемых с акселерометра, установленного на автомобиле. Зависимость ускорения от времени представляет собой быстроизменяющуюся знакопеременную функцию с существенным разбросом значений. Шаг съема данных составлял ![]() .
.
В [3] показано, что процедура прогнозирования непрерывной функции с использованием сглаживающего временного ряда имеет период адаптации, который зависит от точности задания начальных оценок коэффициентов аппроксимации ![]() и
и ![]() в выражении (1). При этом характерно, что неточное задание начального приближения коэффициентов
в выражении (1). При этом характерно, что неточное задание начального приближения коэффициентов ![]() и
и ![]() влияет только на длительность участка адаптации и форму прогнозирующей зависимости
влияет только на длительность участка адаптации и форму прогнозирующей зависимости ![]() на этом участке и практически не влияет на погрешность прогнозирования за его пределами.
на этом участке и практически не влияет на погрешность прогнозирования за его пределами.
Исследования показали, что в рамках выбранной модели временного ряда погрешность прогнозирования за пределами участка адаптации в значительной степени определяется выбором постоянной сглаживания.
На рисунке 1 представлены результаты прогнозирования на время упреждения h экспериментального временного ряда, характеризующего изменение ускорения во времени, при различных значениях постоянной сглаживания α.
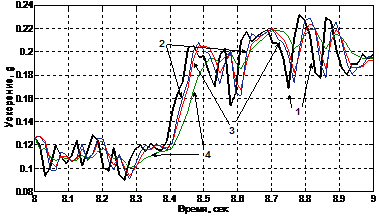
Рисунок 1 – Результаты прогнозирования при различных значениях α: график 1 – экспериментальная зависимость ускорения от времени; график 2 –прогноз при α = 0,55; график 3 - при α=0,35; график 4 - при α=0,15
Анализ графиков показывает, что при увеличении α прогнозирующая кривая точнее воспроизводит форму экспериментальной зависимости. Однако для каждой зависимости существует определенное значение α, определяющее границу возможностей модели в части точности прогнозирования. Погрешности, соответствующие вышеприведенным результатам и иллюстрирующие указанный вывод, представлены на рисунке 2.
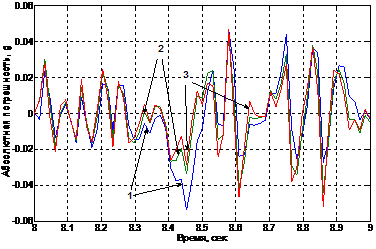
Рисунок 2 – Погрешности прогнозирования при различных значениях α: график 1 –погрешность при α = 0,15; график 2 - при α=0,35; график 3 - при α=0,55
Результаты моделирования показывают, что на участках с резким ростом контролируемого параметра (рис. 1, временной интервал от 8,4 до 8,5 сек.) меньшую погрешность прогнозирования дает модель с высоким значением постоянной сглаживания и, наоборот, в случае небольших колебаний параметра снижение погрешности прогнозирования связано с уменьшением постоянной сглаживания (например, участок от 8,0 до 8,4 сек., рис.1).
C помощью модели можно осуществлять прогнозирование на время упреждения ![]() > h. Результаты прогнозирования для различных
> h. Результаты прогнозирования для различных ![]() при постоянной сглаживания α=0,35 представлены на рисунке 3.
при постоянной сглаживания α=0,35 представлены на рисунке 3.
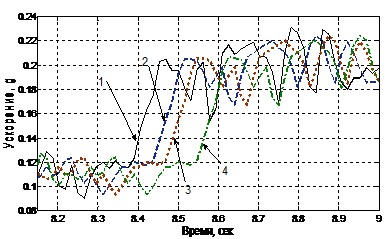
Рисунок 3 – Результаты прогнозирования при α=0,35 и различных значениях ![]() : график 1 – экспериментальная зависимость ускорения от времени; график 2 –прогноз для
: график 1 – экспериментальная зависимость ускорения от времени; график 2 –прогноз для ![]() ; график 3 – для
; график 3 – для ![]() ; график 4 - для
; график 4 - для ![]()
Анализ результатов моделирования показал, что графики прогноза для различных значений времени упреждения в целом повторяют форму экспериментальной кривой с запаздыванием, которое тем больше, чем больше значение времени упреждения. Для участков с длительным по времени (более 4-5h) ростом или уменьшением ускорения, например, для участка, определяемого временным интервалом от 8,4 до 8,5 сек. (рис. 1), время запаздывания прогноза пропорционально времени упреждения (рис.4).
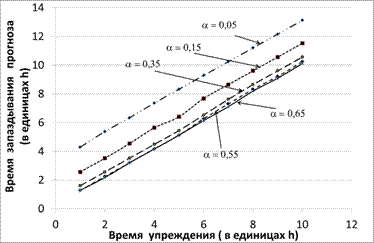
Рисунок 4 – Зависимость времени запаздывания прогноза от времени упреждения в единицах h при различных значениях постоянной сглаживания
Погрешности прогнозирования на участках с длительным по времени ростом или уменьшением ускорения максимальны для графика, соответствующего ![]() , а на участках с незначительно меняющимся трендом погрешности прогнозирования для того же графика в целом меньше по сравнению с другими прогнозирующими кривыми, соответствующими
, а на участках с незначительно меняющимся трендом погрешности прогнозирования для того же графика в целом меньше по сравнению с другими прогнозирующими кривыми, соответствующими ![]() (рис.5).
(рис.5).
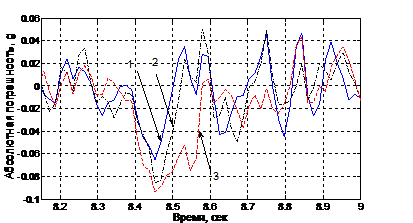
Рисунок 5 – Погрешности прогнозирования при α=0,35 и различных значениях ![]() : график 1 - прогноз для
: график 1 - прогноз для ![]() ; график 2 – прогноз для
; график 2 – прогноз для ![]() ; график 3 – прогноз для
; график 3 – прогноз для ![]()
Следует отметить, что время запаздывания прогноза уменьшается с увеличением постоянной сглаживания α. Однако, использование α > 0,5 – 0,55 для снижения времени запаздывания не эффективно (рис.6).
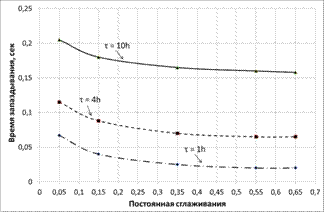
Рисунок 6 – Зависимость времени запаздывания прогноза от постоянной сглаживания при различных значениях времени упреждения
Алгоритм реализации процесса прогнозирования изменения параметра технического объекта
Исследование особенностей модели позволили синтезировать обобщенный алгоритм ее настройки и выполнения прогнозирования:
-
В соответствии с соотношением (1) определяются начальные оценки
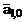 и
и 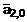 значений коэффициентов
значений коэффициентов 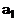 и
и 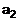 . Для этого используются значения параметра
. Для этого используются значения параметра 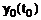 и
и 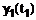 , зафиксированные на начальном этапе настройки модели прогнозирования.
, зафиксированные на начальном этапе настройки модели прогнозирования. -
Устанавливается начальное значение постоянной сглаживания из диапазона [0,15…0,25]. Величина
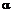 , выбранная из указанного диапазона, может служить точкой отсчета для подбора наиболее подходящего значения
, выбранная из указанного диапазона, может служить точкой отсчета для подбора наиболее подходящего значения 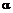 с точки зрения дальнейшей минимизации погрешности прогнозирования контролируемого параметра y в процессе настройки модели.
с точки зрения дальнейшей минимизации погрешности прогнозирования контролируемого параметра y в процессе настройки модели. -
После определения
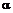 ,
, 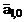 и
и 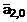 вычисляются
вычисляются 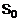 и
и 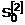 по формуле (4).
по формуле (4). -
Для каждого
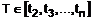 при фиксированном
при фиксированном 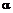 выполняется прогнозирование на время упреждения
выполняется прогнозирование на время упреждения 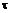 , т.е. прогнозирование на момент времени
, т.е. прогнозирование на момент времени 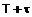 . Прогнозное значение
. Прогнозное значение 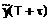 вычисляется по формулам (3) и (2) соответственно. В процессе прогнозирования выделяется участок адаптации, когда прогнозное значение
вычисляется по формулам (3) и (2) соответственно. В процессе прогнозирования выделяется участок адаптации, когда прогнозное значение 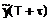 значительно отличаются от измеряемых значений
значительно отличаются от измеряемых значений 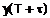 . Участок прогнозирования и, соответственно, окончание участка адаптации, можно определить по поведению прогнозирующей кривой, которая на этом участке стремиться приблизиться к зависимости
. Участок прогнозирования и, соответственно, окончание участка адаптации, можно определить по поведению прогнозирующей кривой, которая на этом участке стремиться приблизиться к зависимости 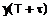 . При этом погрешности прогнозирования в среднем практически не меняются или меняются достаточно медленно по сравнению с динамикой, фиксируемой на участке адаптации.
. При этом погрешности прогнозирования в среднем практически не меняются или меняются достаточно медленно по сравнению с динамикой, фиксируемой на участке адаптации. -
После определения участка прогнозирования необходимо минимизировать погрешности прогнозирования с помощью изменения параметра сглаживания
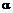 . Увеличивая или уменьшая
. Увеличивая или уменьшая 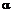 , в зависимости от предполагаемой динамики изменения зависимости
, в зависимости от предполагаемой динамики изменения зависимости 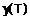 , определим минимальное (ориентировочно) значение погрешности на участке прогнозирования. Параметр сглаживания
, определим минимальное (ориентировочно) значение погрешности на участке прогнозирования. Параметр сглаживания 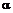 необходимо уменьшать, если прогнозируется медленно меняющаяся зависимость и увеличивать в противном случае. Полученное значение
необходимо уменьшать, если прогнозируется медленно меняющаяся зависимость и увеличивать в противном случае. Полученное значение 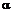 может быть использовано для дальнейшего прогнозирования значений
может быть использовано для дальнейшего прогнозирования значений 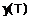 с помощью модели сглаживающего временного ряда
с помощью модели сглаживающего временного ряда 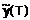 .
.
Выводы
Таким образом, разработана модель и алгоритм краткосрочного прогнозирования изменения быстроизменяющейся физической величины, характеризующей состояние технического объекта. Определены особенности настройки и использования модели, в частности, для обеспечения хорошей точности прогнозирования необходимо выбрать постоянную сглаживания, соответствующую динамике прогнозируемого процесса, для устранения или максимального сокращения участка адаптации временного ряда и расширения участка прогнозирования следует точно задавать начальные значения коэффициентов аппроксимации исходной зависимости. Также определены ограничения модели.
Приведенные соотношения и схема краткосрочного прогнозирования ориентированы на выполнение обработки данных в микроконтроллере микропроцессорного модуля в реальном времени. Моделирование показало эффективность предлагаемого подхода к прогнозированию изменения параметров объекта. Результаты работы могут быть полезны при разработке программно-алгоритмических средств систем мониторинга и обеспечения безопасности технических, например, систем активной безопасности и инерциальной навигации автомобиля.
Результаты исследований изложенные в данной статье получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта "Создание высокотехнологичного производства по изготовлению информационно-телекоммуникационных комплексов спутниковой навигации ГЛОНАСС/GPS/Galileo" по постановлению правительства №218 от 09.04.2010
СПИСОК ЛИТЕРАТУРЫ
1.Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов. – М.: Финансы и статистика, 2003. –416с.
2.Бокс Дж., Дженкинс Г. Анализ временных рядов, прогноз и управление. – М.: Мир, 1974. – 197с.
3.Клевцов С.И. Особенности выбора параметров настройки модели сглаживающего временного ряда для осуществления краткосрочного прогнозирования изменения физической величины.// Известия ЮФУ. Технические науки. 2011. №5(118). – С. 133-138.