Исследование деформирования частично заглубленного фундамента при гармоническом воздействии с использованием метода граничных элементов и метода конечных элементов

Аннотация

М.И. Кадомцев

  Рассмотрен алгоритм совместного использования метода граничных элементов и метода конечных элементов при расчете заглубленного основания в трехмерной постановке. Приведен пример расчета частично заглубленного фундамента, лежащего на трехслойном полупространстве. Проанализированы распределения перемещений под фундаментом в зависимости от частоты воздействия и сочетания физических параметров упругих слоев и упругого полупространства.

Ключевые слова: динамика, вибрация, гармонические колебания, МГЭ, МКЭ

05.23.17 - Строительная механика

В настоящей работе рассматривается воздействие осциллирующей сосредоточенной нагрузки на фундамент, устроенный на слоистом грунтовом основании с использованием гибридного  метода МКЭ-МГИУ[3].
Следует отметить, что, с одной стороны, данная задача представляет практический интерес сама по себе – например, при моделировании воздействия от бура, гидромолота или вибратора для погружения обсадных труб при обустройстве вибронабивных свай на фундаменты зданий. В перечисленных случаях, как показывают неоднократные эксперименты, возможно представление воздействия как сосредоточенной, осциллирующей силы.
С другой стороны, другие, наиболее распространенные источники техногенного воздействия – проезд автомобильного транспорта, железнодорожного транспорта, забивка свай, производство взрывных работ, также могут быть успешно смоделированы с использованием решения задачи в данной постановке. В этих случаях отклик на нестационарное воздействие можно представить как суперпозицию решений стационарных задач с привлечением методов гармонического анализа.
Наиболее актуально решение исследуемой задачи при строительстве зданий и сооружений в условиях плотной городской застройки. В последние годы, несмотря на некоторое снижение объемов строительства вследствие финансового кризиса, количество возводимых в черте города зданий остается очень высоким. В таких условиях является очень актуальной возможность смоделировать влияние техногенных воздействий при производстве строительных работ на фундаменты близлежащих зданий с учетом реальных грунтовых условий. В настоящий момент методики, позволяющие адекватно смоделировать динамическое воздействие и учесть его при проектировании, практически отсутствуют.
1. Постановка задачи
Рассматриваемая область представляет собой с (рис. 1)
Перемещение точек среды удовлетворяют уравнениям Ламе
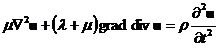   (1)
где  - оператор Лапласа.
При рассмотрении  задачи будем считать, что заданы  условия жесткой стыковки слоев слоистого полупространства, фундамента и здания между собой, что соответствует требованию непрерывности перемещений и напряжений при переходе через границу раздела сред. Следует отметить, что область приложения нагрузки и тип фундамента не влияют на дальнейшие рассуждения.
Исследуемая область (рис. 1) представляет собой фундамент, лежащий на слоистом грунтовом основании. Грунтовое основание рассматривается как пакет из двух слоев, лежащих на однородном полупространстве. Фундамент моделируется прямоугольным параллелепипедом, частично заглубленным в верхний слой.
На поверхности среды вне фундамента задана сосредоточенная сила, осциллирующая с частотой , симметрично относительно фундамента.
При моделировании фундамента с помощью метода конечных элементов использовались восьмиузловые трехмерные конечные элементы в форме прямоугольных параллелепипедов.
Граница стыковки методов МКЭ и МГИУ совпадает с границей раздела фундамента и верхнего слоя грунтового основания.

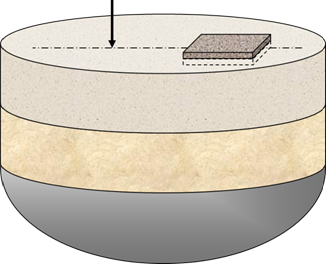
Рис. 1
Исследуемая область  (пространственная задача)

Физические свойства слоев, используемые для каждого из случаев, приведены в таблице 3. Механические характеристики верхнего слоя остаются неизменными при всех вариантах расчета.толщина слоев для всех случаев также постоянна и составляла 6м для первого от дневной поверхности слоя, и 3 м для второго.
Результаты расчета приведены на рис. 2-4.
На рисунках графики, соответствующие однородному полупространствам и структурам «жесткий-мягкий-жесткий» и «мягкий-жесткий-мягкий»  обозначены как «opp», «zmz» и  «mzm» соответственно.
Таблица 1

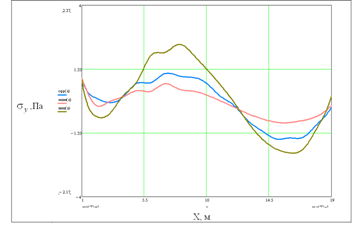
Рис. 2
Распределение напряжений  под бетонным фундаментом. Частота воздействия f=18 Гц,  распределение вдоль центральной линии фундамента

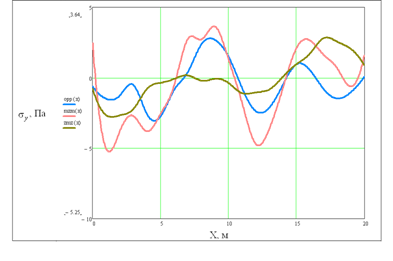
Рис. 3
Распределение напряжений  под бетонным фундаментом. Частота воздействия f=50 Гц,  распределение вдоль центральной линии фундамента

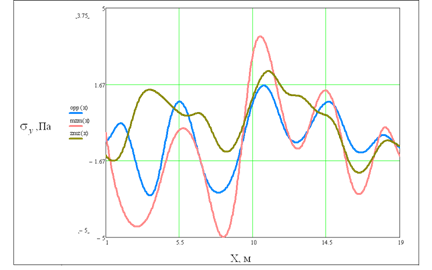
Рис.4
Распределение напряжений  под бетонным фундаментом. Частота воздействия f=100 Гц, распределение вдоль центральной линии фундамента

По результатам исследования можно сделать выводы, что

1. С ростом частоты амплитуда перемещений и напряжений падает.
2. На всех частотах, кроме частоты f=50 Гц, амплитуда напряжений и перемещений наибольшая для структуры «жесткий-мягкий-жесткий»

На частоте f=50 Гц, являющейся резонансной для структуры «мягкий-жесткий-мягкий» для этой структуры амплитуда перемещений и напряжений в сравнении с другими рассмотренными структурами максимальна.
Кроме того, видно, что при достаточно высоких частота (>20Гц) распределение перемещений и напряжений под фундаментом имеет существенный сдвиг фаз по ширине фундамента. Из этого следует сделать вывод, что при исследовании относительно высокочастотного воздействия необходимо принимать во внимание сдвиг фаз.

Литература

1.Бабешко, В.А. Динамика неоднородных линейно-упругих сред / Бабешко, В.А., Глушков, Е.В., Зинченко, Ж.З.. – М.: Наука; Главная редакция физико-математической литературы. 1989. – 343 с.
2.Ляпин, А.А  Механико-математические модели в задачах активной сейсмологии / Ляпин, А.А., Селезнев, М.Г., Собисевич, Л.Е., Собисевич, А.Л. – М.: ГНИЦ ПГК (МФ) при КубГУ Минобразования России, 1999. – 249 с.
3.Кадомцев, М.И. Исследование динамикизаглубленных фундаментов методами граничных и конечныхэлементов / Кадомцев, М.И., Ляпин, А.А., Селезнев, М.Г.//  Строительная механика ирасчет сооружений. – 2010. – № 3. – С.61–64.