Многоспектральный оптической метод формирования и обработки изображений низкоконтрастных образований при априорной неопределённости параметров кожи
Аннотация
Дата поступления статьи: 13.11.2013Для формирования и восстановления изображения подкожного слоя разработаны усовершенствованный многоспектральный метод на основе функции расстройки и алгоритм его реализующий. Метод уменьшает искажающее влияние изменения характеристик кожи на формирование изображения. Использование функции расстройки позволяет произвести обработку без соблюдения жестких требований к точности выбора длин волн, на которых формируются изображения и, соответственно, обеспечения заданного значения отношения значений оптических толщ кожи.
Ключевые слова: Восстановление изображения, многоспектральный метод, функция расстройки, оптическая толща, коэффициент отражения
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
В настоящее время при обнаружении оптической системой низкоконтрастных объектов через рассевающий среды применяются следующие методы и способы фильтрации изображений: импульсная лазерная подсветка с временным стробированием отраженного сигнала [1], нерезкого маскирования, гомоморфной и адаптивной фильтрации [2-5]. Также известны способы коррекции искаженных атмосферой изображений, в том числе многоспектральные, использующие различного рода априорные сведения [6,7]. Общим недостатком существующих систем является то, что они не учитывают влияние неоднородности характеристик рассеивающей среды, что ограничивает их применение и может приводить к наблюдению ложных образований.
Многоспектральный метод восстановления изображений [8,9] основан на свойстве спектральной прозрачности рассеивающей среды в приближении однократного рассеяния. Наиболее важным параметром характеризующим ослабление света в среде за счёт его поглощения и рассеяния является оптическая толща ![]() , величина которой зависит от спектральной прозрачности и толщины среды. Многоспектральный метод использует зависимость оптической толщи
, величина которой зависит от спектральной прозрачности и толщины среды. Многоспектральный метод использует зависимость оптической толщи ![]() от длины волны и поэтому может работать при резких пространственных колебаниях плотности искажающей рассеивающей среды.
от длины волны и поэтому может работать при резких пространственных колебаниях плотности искажающей рассеивающей среды.
Реализация многоспектрального метода при обнаружении низкоконтрастных подкожных образований затруднена тем, что необходимо знать значение величины ![]() для каждой точки поверхности кожи.
для каждой точки поверхности кожи.
В статье рассматривается возможность реализации многоспектрального метода позволяющего произвести обработку без соблюдения жестких требований к точности выбора длин волн, на которых формируются изображения и, соответственно, обеспечения заданного значения отношения значений оптических толщ кожи.
Рассмотрим особенности реализации многоспектрального метода.
Обследуемый подкожный участок, характеризуемый коэффициентами отражения![]() подсвечивается одновременно лазерными (светодиодными) лучами на двух длинах волн
подсвечивается одновременно лазерными (светодиодными) лучами на двух длинах волн![]() и
и![]() .Изображение подсвечиваемого участка поверхности воспринимается двумя матрицами фоточувствительных приборов с зарядовой связью (ФПЗС) для
.Изображение подсвечиваемого участка поверхности воспринимается двумя матрицами фоточувствительных приборов с зарядовой связью (ФПЗС) для![]() и
и![]() , причем каждый элемент матриц воспринимает изображение определенного элемента подсвечиваемого участка.
, причем каждый элемент матриц воспринимает изображение определенного элемента подсвечиваемого участка.
Для определения заряда![]() , накопленного в ячейке ФПЗС при наблюдении объекта через рассеивающие среды (кожу), расположенного в непосредственной близости к рассеивающей среде, воспользуемся следующим выражением [1]:
, накопленного в ячейке ФПЗС при наблюдении объекта через рассеивающие среды (кожу), расположенного в непосредственной близости к рассеивающей среде, воспользуемся следующим выражением [1]:
![]() ,
,
где ![]() - чувствительность ячейки, зависящая в основном от коэффициента пропускания многослойного покрытия, квантового выхода, внутреннего фотоэффекта и коэффициента поглощения полупроводниковой подложки;
- чувствительность ячейки, зависящая в основном от коэффициента пропускания многослойного покрытия, квантового выхода, внутреннего фотоэффекта и коэффициента поглощения полупроводниковой подложки;
![]() - световой поток, излучаемый квантовым генератором на элемент участка поверхности,
- световой поток, излучаемый квантовым генератором на элемент участка поверхности,
![]() - время накопления,
- время накопления,
![]() - диаметр объектива фотоприемника,
- диаметр объектива фотоприемника,
![]() - расстояние от точки визирования до фотоприемника,
- расстояние от точки визирования до фотоприемника,
![]() - оптическая толща рассевающей среды,
- оптическая толща рассевающей среды,
![]() - безразмерный коэффициент, характеризующий отражательную способность и рельеф объекта [10].
- безразмерный коэффициент, характеризующий отражательную способность и рельеф объекта [10].
Так как ![]() величина постоянна, то ее можно обозначить через m.
величина постоянна, то ее можно обозначить через m.
Получим ![]() ,(1)
,(1)
Для решения данной задачи составим систему уравнений при![]() , где
, где ![]() - постоянный коэффициент, принимающий значения от 1 до 2,
- постоянный коэффициент, принимающий значения от 1 до 2,
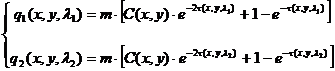 ,(2)
,(2)
Для дальнейшего анализа введем упрощенную систему обозначений
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
Тогда система (2) примет вид
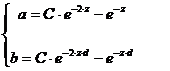 ,(3)
,(3)
Аналитическое решение системы (3) возможно при d=2,
В этом случае оценочные значения ![]() и
и ![]() рассчитывались по следующим формулам:
рассчитывались по следующим формулам:
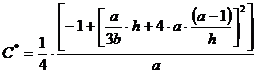 , (4)
, (4)
где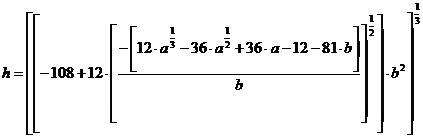
![]() (5)
(5)
![]() , (6)
, (6)
Рассмотренный метод предполагает наличие априорных данных о взаимосвязи оптических толщ кожи на ![]() и
и ![]() что при обнаружении подкожных образований является затруднительным.
что при обнаружении подкожных образований является затруднительным.
Поэтому необходимо произвести предварительную оценку значения оптической толщи в разных точках обследуемого участка. Для этого исключим из анализа значение коэффициент отражения С. В первом уравнении системы (3) примем, что![]() . Тогда получим оценку значения z оптической толщи:
. Тогда получим оценку значения z оптической толщи:
![]() (7)
(7)
Оценка значения оптической толщи будет наиболее сильно отличаться от реального значения при ![]() равным 0 или 1. Оценим погрешность определения оптической толщи по выражению (7). Для этого при заданных значениях
равным 0 или 1. Оценим погрешность определения оптической толщи по выражению (7). Для этого при заданных значениях ![]() и
и ![]() по первому уравнению системы (3) рассчитывается значение
по первому уравнению системы (3) рассчитывается значение ![]() и подставляется в выражение (7), полученный результат сравним с заданным значением
и подставляется в выражение (7), полученный результат сравним с заданным значением ![]() . Погрешность оценки значения оптической толщи оказалась одинаковой для случаев, когда
. Погрешность оценки значения оптической толщи оказалась одинаковой для случаев, когда ![]() равного 0 и 1 (рисунок 1).
равного 0 и 1 (рисунок 1).
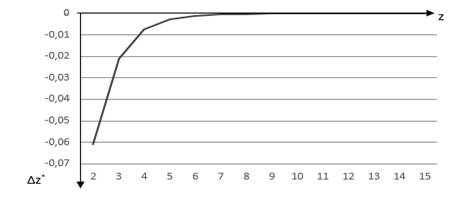
Рисунок 1 - Погрешность оценки значения оптической толщи
Из представленной зависимости видно, что погрешность оценки не превышает 7%. Данная погрешность ![]() оценки оптической толщи высока для правильного определения значений коэффициентов отражения, но достаточна для того, чтобы разбить обследуемый участок на участки с одинаковыми оптическими толщами.
оценки оптической толщи высока для правильного определения значений коэффициентов отражения, но достаточна для того, чтобы разбить обследуемый участок на участки с одинаковыми оптическими толщами.
Кроме того, выражение (7) можно будет использовать в дальнейшем для получения оценочного значения коэффициента ![]() .
.
Введем понятие функция расстройки (ФР). ФР определяет зависимость результата оценки значения оптической толщи ![]() в результате решения системы (3)при несоблюдении требования d=d0, где d0 – требуемое значение d.В случае расстройки будем задавать значение
в результате решения системы (3)при несоблюдении требования d=d0, где d0 – требуемое значение d.В случае расстройки будем задавать значение
![]() , (8)
, (8)
где ![]() - коэффициент расстройки, принимающий значение от -0,9 до 1.
- коэффициент расстройки, принимающий значение от -0,9 до 1.
Введение расстройки приводит к нарушению условий, прикоторых справедливо выражение (4)и появлению комплексных значений С*. Проведенные исследования показали, что для устранения данных ошибок достаточно взять ![]() .
.
Рассмотрим поведение ФР.
Для чего при заданных значениях Z и C по выражениям системы (3) рассчитаем значения a и b, с учетом коэффициента расстройки, и подставим в выражения (4-6).
На рисунке 2 представлена зависимость результата вычисления ![]() при изменении коэффициента расстройки при заданных значениях d0=2, z=1,5;3;4,5;6.
при изменении коэффициента расстройки при заданных значениях d0=2, z=1,5;3;4,5;6.
Анализ полученных зависимостей привел к выводу о прямой связи угла наклона возрастающей части линий со значением z для λ1.
Используем этот участок функции для вычисления значения C. Значения первой производной возрастающего участка постоянны, что свидетельствует о линейности функции расстройки.
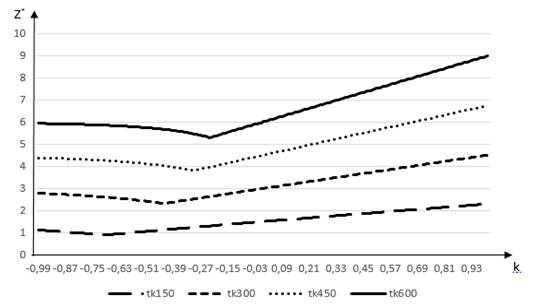
Рисунок 2 –Функция расстройки tk150, tk300, tk450, tk600 соответственно при заданных значениях z=1,5;3;4,5;6.
Сформируем изображения на четырех длинах волн![]() ,
,![]() ,
,![]() ,
,![]() . Причем значение
. Причем значение ![]() подбирается с использованием выражения (7) таким образом, чтобы значение d было ≥2 (что соответствует значению k≥0), а значения
подбирается с использованием выражения (7) таким образом, чтобы значение d было ≥2 (что соответствует значению k≥0), а значения ![]() и
и ![]() Для каждой точки двух изображений, полученных соответственно на
Для каждой точки двух изображений, полученных соответственно на ![]() и
и![]() ,
, ![]() и
и![]() ,
, ![]() и
и ![]() . по выражению (6) вычисляются значения
. по выражению (6) вычисляются значения![]() ,
, ![]() и
и![]() , В результате получаются три точки, располагающиеся на возрастающей линии ФР, при значениях коэффициентов расстройки
, В результате получаются три точки, располагающиеся на возрастающей линии ФР, при значениях коэффициентов расстройки![]()
![]() ,и
,и ![]() (рисунок 3).
(рисунок 3).
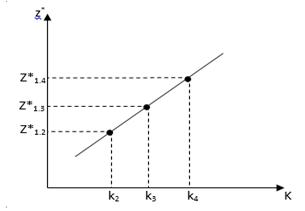
Рисунок 3 – Функция расстройки для дискретных значений λ
Для этих точек будет справедливо следующее равенство:
![]() . (9)
. (9)
Преобразуем отношение![]() с учетом выражения (8). После преобразования получим
с учетом выражения (8). После преобразования получим![]() , где z2, z3, z4 – значения z соответственно для λ2, λ3, λ4.
, где z2, z3, z4 – значения z соответственно для λ2, λ3, λ4.
Используя совместно равенство (9) и первое уравнение системы (3) можно определить значение C. Рассчитаем значение левой части равенства (9). Зададим значение. С=0,5, вычислим значения z2, z3, z4, из первого уравнение системы(3)и проверим выполнение равенства (9). При невыполнении равенства задается другое значение. С и повторяются предыдущие действия. Методом перебора выбирается такое значение. С, при котором выполняется равенство (9).
Разработанный метод, реализуется в алгоритме, представленном на рисунке 4.
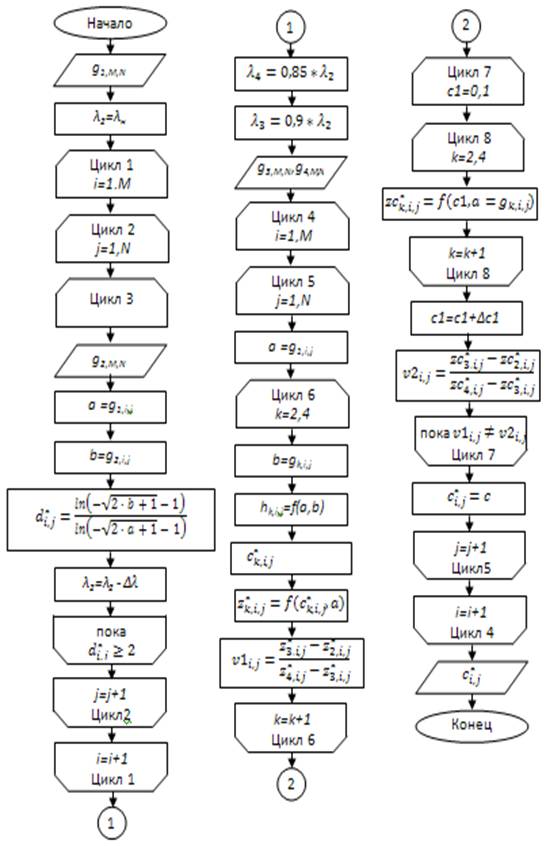
Рисунок 4 – Алгоритм обработки изображения
В алгоритме используются данные нескольких изображений![]() , где l – номер длины волны, на которой сформировано изображение;i,j–номер точки изображения, соответственно, по координатам x и y. На первом этапе обработки в циклах 1-3 для каждой точки изображений
, где l – номер длины волны, на которой сформировано изображение;i,j–номер точки изображения, соответственно, по координатам x и y. На первом этапе обработки в циклах 1-3 для каждой точки изображений![]() и
и![]() производится подбор значения длины волны
производится подбор значения длины волны![]() .Начиная с
.Начиная с ![]() для точки 0,0 проверяется выполнение условия d≥2. При невыполнении условия значение
для точки 0,0 проверяется выполнение условия d≥2. При невыполнении условия значение ![]() уменьшается, что приводит к увеличению значения d. Вводятся данные изображения, полученного на новой длине волны и снова проверяется условие и так до его выполнения. Для следующей точки изображения значение
уменьшается, что приводит к увеличению значения d. Вводятся данные изображения, полученного на новой длине волны и снова проверяется условие и так до его выполнения. Для следующей точки изображения значение ![]() не сбрасывается. Таким образом, выбирается такое значение
не сбрасывается. Таким образом, выбирается такое значение ![]() при котором условие d≥2 выполняется для каждой точки изображения. Рассчитываются значения
при котором условие d≥2 выполняется для каждой точки изображения. Рассчитываются значения ![]() и
и![]() . Их значения выбираются так, чтобы значения оптических толщ возрастали. Далее в цикле 6 для каждой точки изображений по уравнениям (4-6) находятся значения
. Их значения выбираются так, чтобы значения оптических толщ возрастали. Далее в цикле 6 для каждой точки изображений по уравнениям (4-6) находятся значения![]()
![]() и
и ![]() и рассчитывается значение левой части равенства (9). В циклах 7-8 производится вычисление значения правой части равенства (9) при разных значениях. С= с1. Результатом являются значения,
и рассчитывается значение левой части равенства (9). В циклах 7-8 производится вычисление значения правой части равенства (9) при разных значениях. С= с1. Результатом являются значения, ![]() для которых выполняется равенство (9). Таким образом, разработаны многоспектральной метод и алгоритм его реализующий, позволяющие уменьшить искажающее влияние изменения характеристик кожи на формирование изображения. Использование функции расстройки позволяет произвести обработку без соблюдения жестких требований к точности выбора длин волн, на которых формируются изображения и, соответственно, обеспечения заданного значения отношения значений оптических толщ кожи d=d0. Дальнейшее направление развития многоспектрального метода предполагается связать с линеаризацией функции расстройки в сторону отрицательных значений расстройки и использования нелинейной части эти функции
для которых выполняется равенство (9). Таким образом, разработаны многоспектральной метод и алгоритм его реализующий, позволяющие уменьшить искажающее влияние изменения характеристик кожи на формирование изображения. Использование функции расстройки позволяет произвести обработку без соблюдения жестких требований к точности выбора длин волн, на которых формируются изображения и, соответственно, обеспечения заданного значения отношения значений оптических толщ кожи d=d0. Дальнейшее направление развития многоспектрального метода предполагается связать с линеаризацией функции расстройки в сторону отрицательных значений расстройки и использования нелинейной части эти функции
Литература:
1. Карасик В.Е., Бокшанский В.Б. Управление временными режимами работы ЛСВ с импульсным подсветом // Приборы и системы управления. 1998. №3. С.85–87.
2. Стокхэм Д. Обработка изображений в контексте модели зрения // ТИИЭР. 1972. Т.60, №7. C.93 –107.
3. Прэтт У. Цифровая обработка изображений: пер с англ. М.: Мир, 1982. 480с.
4. Tamar, P. Adaptive filtering of image. Institution of Radioengineering / P. Tamar, J. Lim // IEEE Proceeding. 1981. Vol.1, №1-4.P.1–8.
5. A. J. LaRocca and R. E. Turner, "Atmospheric Transmittance and Radiance: Methods of Calculation," IRIA State-of-the-Art Report, ERIM 107600-10-T (Environmental Research Institute of Michigan, Ann Arbor, 1975); also available from NTIS as AD-A017 459.
6. Протасов К.Т., Белов В.В., Артамонов Е.С. Адаптивное восстановление космических снимков подстилающей поверхностиЗемли с использованием априорной информации // Вычислительные технологии. Т.5: Спец. выпуск. 2000. С.69 –81.
7. Муравьев И.В., Перцев Л.В., Исаенков Н.С. Обзор методов адаптивного использования спектра [Электронный ресурс] // «Инженерный вестник Дона», 2011, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2011/468, свободный. – Загл. с экрана– Яз. Рус.
8. Куликов А.Ю., Каверина Л.В., Строев В.М. Восстановление изображений, полученных активной телевизионной системой при работе в сложных метеоусловиях // Радиосистемы. 2003. Вып. 70, №6.С. 45-48.
9. Строев В.М., Альмас Г.Ф., Истомина А.И. Многоспектральный оптический метод обнаружения объектов через неоднородные среды//Вестник Иркутского Государственного Технического Университета. 2013. №6. С.160-165.
10. Благородова Н.В., Замятин А.В., Сухомлинова В.В. Алгоритм расчёта отражений на основе геометрической модели [Электронный ресурс] // «Инженерный вестник Дона»,. 2012, №4 (часть 1). – Режим доступа:
http://www.ivdon.ru/magazine/archive/n4p1y2012/1079, свободный. – Загл. с экрана– Яз. Рус.