Влияние вариаций входных параметров на режим работы теплообменной системы
Аннотация
Дата поступления статьи: 18.11.2013"Динамический режим работы теплообменников характерен для ряда технологических тепловых установок, а так же систем воздушного отопления, вентиляции и кондиционирования воздуха. Технологически заданный алгоритм управления режимом работы теплообменников на практике реализуется средствами ручного или автоматического регулирования по одному или нескольким управляющим параметрам. Очевидно, что наиболее эффективный в энергетическом и технико-экономическом отношении алгоритм управления динамическим режимом работы теплообменника может быть выявлен только в виде анализа соответствующей математической модели. В статье рассматривается математическая модель динамического режима работы системы теплообменников с естественной циркуляцией воздуха. В качестве входных параметров рассматриваются температуры холодного и горячего потоков воздуха. Моделируются изменения на входах теплообменников и находятся пределы, в которых эти изменения не повлияют на работу всей системы. Для того чтобы температура на i-том ТО не изменилась, коэффициент изменения должен стремиться к нулю, так как все остальные величины ограничены техническими параметрами системы. "
Ключевые слова: потери теплоты в окружающую среду, начальная температура горячего (холодного) потока, конечная температура горячего (холодного) потока, пределы изменения горячего, холодного потока
05.13.01 - Системный анализ, управление и обработка информации (по отраслям)
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Динамический режим работы теплообменников характерен для ряда технологических тепловых установок, а так же систем воздушного отопления, вентиляции и кондиционирования воздуха. Технологически заданный алгоритм управления режимом работы теплообменников на практике реализуется средствами ручного или автоматического регулирования по одному или нескольким управляющим параметрам. Очевидно, что наиболее эффективный в энергетическом и технико-экономическом отношении алгоритм управления динамическим режимом работы теплообменника может быть выявлен только в виде решения соответствующей математической модели.
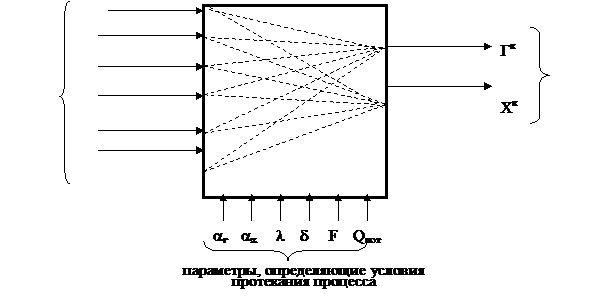
В [1] рассматривается математическая модель динамического режима работы теплообменников. Информационная структура процесса теплообмена представлена следующей схемой, рис.1.
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Рис.1. Схема информационной структуры теплообмена.
aг (aх) – коэффициенты теплопередачи со стороны горячего (холодного) потока
δ- толщина стенки
λ- теплопроводность стенки
F- поверхность теплообмена
Qпот –потери теплоты в окружающую среду.
Гн (Хн) – начальная температура горячего (холодного) потока.
Гк (Хк) – конечная температура горячего (холодного) потока.
Gг (Gх)-массовый расход горячего ( холодного ) потока
сг (сх) – теплоёмкость горячего ( холодного ) потока.
Упрощенная схема процесса передачи теплоты на I-той ступени предлагается в [2 ].
![]() (1)
(1)
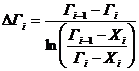 (2)
(2)
![]() (3)
(3)
![]() (4), где
(4), где
Qi –количество теплоты передаваемой холодному потоку на I-той ступени,
λi-теплоёмкость горячего потока,
Wi-водяной эквивалент горячего потока,
Гi (Хi)-температура горячего ( холодного ) потока на I-той ступени, рис.2.
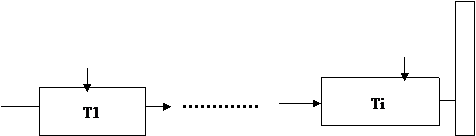
Х1 Хi G
Г1 Гi
Рис.2. Схема теплообменной системы с естественной циркуляцией продуктов сгорания.
Предлагаемый в [2] подход позволяет получить решения, определяющие влияние величины изменения входных параметров среды на ее выходные параметры.
Решим (1), (2), (4) откуда
![]() , (5)
, (5)
где 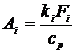
Рассмотрим изменения входных параметров в уравнении (5). Найдем интервалы в пределах, которых температура горячего потока Гi не будет меняться.
![]() Пусть G
Пусть G![]() =G+ΔG. Исследуем изменения в уравнении (5)
=G+ΔG. Исследуем изменения в уравнении (5)
(6)
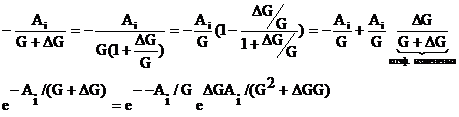
Для того чтобы температура на i-том ТО не изменилась, коэффициент изменения должен стремиться к нулю, так как все остальные величины ограничены техническими параметрами системы. Пусть он будет равен a, где a- величина бесконечно малая и стремится к нулю. Тогда, если массовый расход горячего потока изменится на величину
![]()
температура на i-том ТО останется неизменной. Решив неравенство относительно ΔG получим:
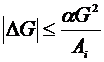
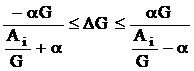 .
.
При α→0 интервал изменения для ΔG ,
Очевидно, что изменения в пределах этого интервала не повлияют на температуру горячего потока.
Пусть температура горячего потока на предыдущей ступени изменится на Δi-1 , как это повлияет на i-тый ТО?
![]()
![]()
Подставив значения в уравнение (5), получим
![]() , (7)
, (7)
После преобразования получим линейную зависимость Гi от Δi-1.
![]() .
.
Найдем пределы изменения для Δi-1
![]() .
.
![]() Рассмотрим случай изменения температуры холодного потока Х
Рассмотрим случай изменения температуры холодного потока Х![]() на величину Δ
на величину Δ
![]() . (8)
. (8)
После преобразования
![]() ,
,
откуда интервал для Δ
![]()
Зависимости (6),(7),(8) устанавливают так же интервалы изменения параметров теплообменивающихся сред, при которых изменение выходных параметров не превышает заданных значений.
Литература:
- Кафаров В. В., Мешалкин В. П., Гурьева Л. В. Оптимизация теплообменных процессов и систем. – М.: Энергоатомиздат, 1988, 191 с.
- Каневец Г.Е., Обобщенные методы расчета теплообменников. – К.: Наук. думка, 1979, 352 с.
- Василенко А.И., Новгородский Е.Е. Оптимизация аэродинамических систем комплексного использования теплоты [Тескт]: Монография/ А.И. Василенко – Ростов-н/Д,: Рост. гос. строит. ун–т, 1999. – 175с.
- Гапонов В.Л., Медиокритский Е.Л., Новгородский Е.Е. Зашита окружающей среды при технологическом использовании продуктов сгорания теплообменными системами [Тескт]: Монография/В.Л. Гапонов. – РГАСХМ. Ростов н/Д, 1998. –268с. – ISBN 5-89071-042-7
- Новгородский Е.Е., Василенко А.И., Корабельников Е.Г. Оптимизация поперечных сечений линий связи установок комплексного использования теплоты [Текст]// Проблемы энергосбережения и экологии при использовании углеводородных топлив. Сборник трудов международной конференции. Часть 1. – Ростов-на-Дону: Рост.гос. строит. ун-т. 2000. – с.66–70.
- Новгородский Е.Е., Василенко А.И., Корабельников Е.Г. Расчет оптимальных конструкционных параметров теплообменных аппаратов [Текст]// В сб. Седьмая Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов. М.: ТВП, 2000, с.397-398.
- Смирнов Р.В., Бахвалов Б.Ю. Математическое моделирование теплообменных процессов в энергосберегающих гелиоустановках. Республики [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/677 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Grantham Stephanie, Household energy consumption, conservation & efficiency. Literature Review / Alice Solar City: Literature Review, 2010. 43p.(http://www.alicesolarcity.com.au/sites/default/files)
- Керимов И.А., Дебиев М.В, Магомадов Р. А-М, Хамсуркаев Х.И. Ресурсы солнечной и ветровой энергии Чеченской Республики [Электронный ресурс] // «Инженерный вестник Дона», 2012, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2012/677 (доступ свободный) – Загл. с экрана. – Яз. рус.
- A literature review on Energy Innovation Systems Structure of an emerging scholarly field and its future research directions / Bernhard Truffer, Jochen Markard, Christian Binz, Staffan Jacobsson. – 2012, November. - 40p. (http://www.eis-all.dk/upload/eis/eis_radarpaper_final.pdf).