Математическое моделирование диагностического сигнала при оценке состояния электроприводной арматуры по сигналу тока двигателя
Аннотация
Статья посвящена разработке диагностической модели, обосновывающей выявление дефектов по сигналам тока электромеханического оборудования, содержащего информацию о линейных и нелинейных процессах в объекте. Сопоставление результатов численного моделирования и натурных экспериментов позволяет сделать вывод об адекватности модели. Возможно применение данной модели для формирования эталонных диагностических признаков с целью обучения автоматизированной системы диагностики.
Ключевые слова: техническая диагностика, нелинейный процесс, модуляция, спектральный анализ, математическое моделирование.05.13.18 - Математическое моделирование, численные методы и комплексы программ
При определении технического состояния электроприводной арматуры (ЭПА) в условиях опасных производств (действующей АЭС) затруднено применение контактных методов диагностики в том числе широко распространенного виброакустического метода. В связи с этим существенное развитие получили методы диагностики ЭПА по сигналу тока двигателя арматуры, который можно зарегистрировать в помещениях, предназначенных для постоянного доступа персонала[1].
Особую сложность представляет диагностика механических дефектов, возникновение и развитие которых сопровождается нелинейными процессами[2]. С целью повышения качества диагностирования возможно применение операции моделирования. Модель ЭПА должна отражать наиболее существенные свойства объекта диагностирования: нелинейность проявления возмущающих факторов в приводе; нелинейность восприятия возмущающих факторов системой асинхронного двигателя.
Рассмотрим проявления наиболее распространенных дефектов приводов ЭПА: нарушение геометрии подшипников (раковины, сколы тел и дорожек качения); несоосность валов; нарушение геометрии зубчатых и червячных передач (сколы, зазубрины сопрягаемых деталей). Данные дефекты являются источниками механических колебаний, которые в работе [2] описываются уравнением (1):![]() (1)
(1)
где μi– глубина амплитудной модуляции гармоник ωz частотой iΩ; Ω=fд2Π – круговая частота попадания дефекта в зону контакта; ωz – основная частота возбуждения (зубцовая или подшипниковая); νi – индекс фазовой модуляции; ωш – шумовая составляющая. Исследованиями [3] установлено, что в случае дефекта оборудования, сопровождающегося интенсивными соударениями в механизме (скол, задир), с наибольшей вероятностью наблюдается амплитудная модуляция. Дефект типа заклинивания в большей степени характеризуется фазовой модуляцией. При развитом дефекте может наблюдаться амплитудно-фазовая модуляция. Шумовая составляющая возрастает по мере развития дефекта.
Спектральное представление уравнения (1) имеет вид суммы спектров вынужденных и собственных колебаний:
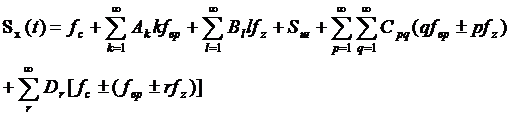 (2)
(2)
где lfz– спектр основных частот; (pfz±qfвр) – спектр комбинационных частот в окрестности частот вращения qfвр; fс±(fвр±rfz) – спектр комбинационных частот в окрестности собственной частоты системы fс; Sш(f) – спектр шума.
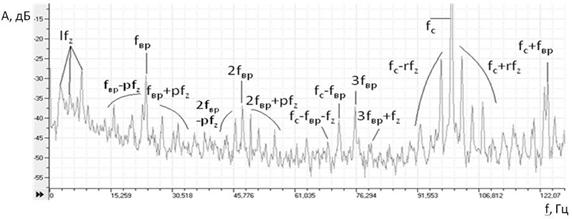
Данные составляющие представлены в спектре виброакустических колебаний ЭПА с дефектом червячного колеса редуктора (рисунок 1). Здесь fврчастота вращения ротора, fz- частота дефектного червячного колеса, fс-сетевая гармоника – 22, 2,5, 100 Гц соответственно.
Выражение (2) характеризует нелинейность проявления дефекта, т.к. отображает перераспределение энергии между частотами результирующего колебательного процесса.При экспериментальном анализе спектров, соответствующих выражению (2) установлено[1,2,3], что значения основных и комбинационных частот несут специфическую информацию о дефекте и позволяют оценить степень развития дефекта.

Колебания (1) передаются по кинематической цепочке к валу электродвигателя и нарушают равномерность вращения ротора. В работе [4] представлены уравнения, отображающие модуляции тока статора в зависимости от поперечных и крутильных колебаний ротора.
При поперечных колебаниях ротора ток фазной обмотки статора IА характеризуется амплитудными модуляциями:
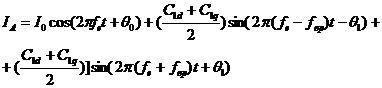 (3)
(3)При крутильных колебаниях ротора ток статора IА характеризуется фазовыми модуляциями:
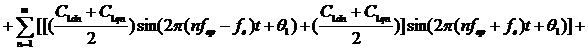
где С1d, С1q, С1dn, С1qn, D1dn, D1qn - амплитуды токов статора и ротора в d и q координатах; I0 – питающий ток; fe, fвр – частота сетевой составляющей, частота вращения ротора. Выражения (3) и (4) возможно использовать при составлении модели диагностического сигнала ЭПА при этом амплитуды гармоник токов статора и ротора можно расценивать как параметры, отражающие возмущения в приводе.
Для построения адекватной модели необходимо учитывать нелинейную зависимость между возмущением, вызванным дефектом в приводе, и реакцией двигателя на данное возмущение[5]. При токе статора, насыщенном гармоникам неравномерно вращающегося ротора (3), (4), в зазоре двигателя возникает множество просторанственно-временных гармоник поля и тока. Наиболее значимыми из которых являются колебания линейной токовой нагрузки вида(5)
и индукции вида(6)![]()
![]()
где A1k –амплитуда линейной плотности k-й гармоники тока статора; Bk – амплитуда индукции k-й гармоники результирующего поля в ВЗ; р – число пар полюсов;φ– координата в ВЗ; под fk понимаются комбинации частот сети и частот вращения ротора;φ1k, φ0k – разность фаз между гармониками тока и индукции.
В результате взаимодействия первой и высшей гармоник поля и тока радиальная вибрация будет возбуждаться силой
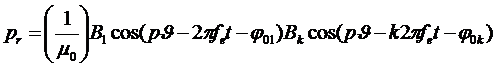 (7)
(7)(μ0 – магнитная постоянная), а тангенциальная – силой
Исходя из выражений (7) и (8) можно прогнозировать при наличии возмущений в приводе возникновение колебаний двигателя на частотах, кратных частоте сети и частоте вращения ротора.
На основании рассмотренных закономерностей 1-8 была построена приближенная качественная модель диагностического сигнала:
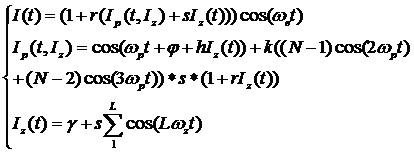
Здесь первое уравнение описывает диагностический сигнал на статорных обмотках ЭД. Оно включает уравнения, описывающие колебания ротора Ip и вынуждающее воздействие со стороны действующего в системе возмущения (дефекта) Iz(t). В данной модели линейному признаку дефекта соответствует частота возмущающего фактора ωz. Нелинейные процессы, связанные с развитием дефектов выражены с помощью следующих параметров: r - коэффициент, отражающий чувствительность двигателя к механическим колебаниям; s - коэффициент, отражающий чувствительность ротора к возмущающим факторам; k – соотношение амплитуд гармоник ротора; L и N – число гармоник вынуждающего воздействия и ротора соответственно; φ – разность фаз между гармониками ротора; γ - шум, возникающий при работе механизма, и связанный с наличием дефекта, входит в виде слагаемого в уравнение колебаний ротора [3]. Информация, представленная в фазо-динамических характеристиках сигнала I(t) определяется сдвигом фаз между гармониками на частоте вращения ротора. При наличии фазовой модуляции сдвиг фаз определяется как постоянной величиной φ, так и действием возмущающего фактора Iz(t). Когда коэффициент фазовой модуляции h равен нулю, сдвиг фаз соответствует постоянной величине. Чувствительность системы двигателя, выраженную параметрами модели, зависит от вида дефекта и степени его развития. На основании анализа процессов, протекающих в ЭПА, были определены параметры, соответствующие состояниям: без дефекта, дефект подшипника двигателя; дефект червячного колеса редуктора (Таблица); несоосность валов двигателя и редуктора; неточность изготовления/сборки зубчатой передачи.
Таблица. Параметры модели, соответствующие дефекту червячного колеса редуктора.
Стадия развития Параметры |
0 |
1 |
2 |
3 |
4 |
5 |
|
L |
0 |
1 |
2 |
3 |
5 |
1 |
|
N |
1 |
1 |
2 |
2 |
2 |
3 |
|
φ, рад |
0 |
0 |
(π/4÷3π/4) ∩ (5π/4÷7π/4) |
(π/4÷3π/4) ∩ (5π/4÷7π/4) |
[-π/4÷π/4] ∩ [3π/4÷5π/4] |
[-π/4÷π/4] ∩ [3π/4÷-5π/4] |
|
γ, А |
0 |
0,01 |
0,02 |
0,025 |
0,05 |
0,1 |
|
s*10-2, А |
0 |
5 |
7 |
10 |
10 |
7 |
|
h, рад/А |
0 |
0 |
0 |
0 |
0 |
0,2 |
|
r*10-2, 1/А |
3 |
7 |
10 |
15 |
20 |
18 |
|
k |
0 |
0 |
0,5 |
0,5 |
1 |
0,7 |
С помощью данной модели были рассчитаны эталонные сигналы ЭПА с наиболее распространенными дефектами. Для проверки адекватности модели на лабораторной установке были получены сигналы ЭПА с аналогичными дефектами.
На рисунке 2 приводится сравнение спектров огибающих эталонного и реального сигналов соответствующих первой стадии дефекта червячного колеса редуктора (скол зуба червячного колеса). Дефект, в соответствии с выражением (2), проявляется в виде гармоник основных частот червячного колеса fz и комбинационных частот в окрестности частоты вращения ротора fвр±fz, и сетевой гармоники fc±fz. При цифровом моделировании использовались модель (9) и параметры Таблицы, соответствующие второй стадии дефекта червячного колеса. Расхождение между расчетными и экспериментальными данными незначительно и обусловлено признаками большей степени развития дефекта в спектре экспериментального сигнала: больший уровень шума, высшие комбинационные гармоники fс±rfz. 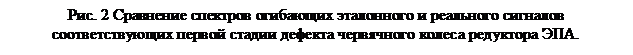
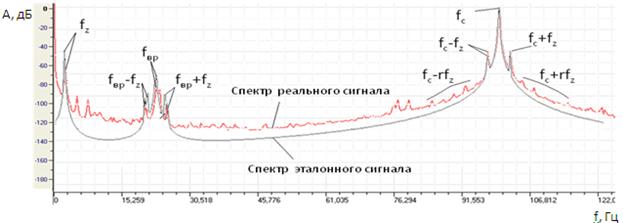
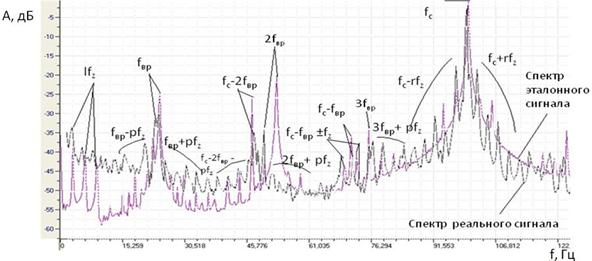
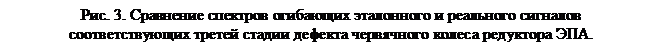
При развитии дефекта (рисунок 3) спектр характеризуется появлением высших гармоник основных lfzи комбинационных fвр±pfz, 2fвр+pfz, 3fвр+pfz, fс±rfz, fс-fвр±fz, fс-2fвр-pfz частот, возрастает уровень шума. Данные особенности соответствуют описанию третей стадии дефекта согласно модели (9) и Таблицы 1. Расхождение между расчетными и экспериментальными данными, обусловлено смещением основных и комбинационных гармоник (до 3 Гц относительно расчетного значения) в спектре сигнала реального объекта.
Для развитого дефекта (рисунок 4) характерен сигнал с высоким уровнем шума. Эталонный сигнал моделировался, как пятая стадия дефекта червячного колеса. Шумовая компонента затрудняет анализ основных fz и комбинационных частот fс±fz, fс-rfвр, частот вращения fвр, 2fвр, 3fвр в спектрах огибающих обоих сигналов.

Основной причиной расхождения расчетных и экспериментальных данных является возросшая в результате развития дефекта нестационарность реального объекта. Данная особенность не поддается прогнозированию с помощью представленной детерминированной модели.
На основании лабораторных и промышленных экспериментов можно сделать вывод об адекватности модели, описывающей сигнал тока ЭПА с учетом технического состояния арматуры. Возможно применение данной модели для формирования эталонных диагностических признаков с целью обучения автоматизированной системы диагностики.
Литература:
- 1.Методика оценки технического состояния электроприводной арматуры РЦ и ТЦ энергоблока №1 по ее электрическим параметрам. ЭМТД 66-019–06 ПМ, Никифоров В.Н., Пугачева О.Ю., Сиротин Д.В. 2006.
2.Методы автоматизированного исследования вибрации машин: справочник/ Добрынин С.А., Фельдман М.С., Фирсов Г.И. – М.: Машиностроение, 1987. – 224 с. с ил. – (Основы проектирования машин).
3.Барков А.В., Баркова Н.А., Азовцев А.Ю. Мониторинг и диагностика роторных машин по вибрации: СПб.: Изд.центр СПбГМТУ, 2000, 169 с.
4.Сипайлов Г.А. и др. Электрические машины (специальный курс) – М.:Высш.шк.,1987. – 287 с.
5.Шубов И.Г. Шум и вибрация электрических машин. - 2-е изд., перераб. и доп. - Л.: Энергоатомиздат, 1986. 208 с. с ил.